我们能够通过分别把两个向量的各个分量相加得到向量之和,注意在相加之前必须保证它们有相同的维数。
u + v =
(ux+ vx,
uy+ vy,
uz+ vz)
图5显示的是几何学上的向量相加。

两个向量相加的代码,我们使用重载的加法操作符:
|
D3DXVECTOR3 u(2.0f, 0.0f,
1.0f);
D3DXVECTOR3 v(0.0f, -1.0f,
5.0f);
// (2.0 +
0.0, 0.0 + (-1.0), 1.0 + 5.0)
D3DXVECTOR3 sum = u + v;
// = (2.0f, -1.0f, 6.0f)
|
和加法类似,通过分别把两个向量的各个分量相减得到向量之差。再次重声两个向量必须是相同维数。
u-v = u + (-v) = (ux
- vx, uy
- vy, uz -
vz)
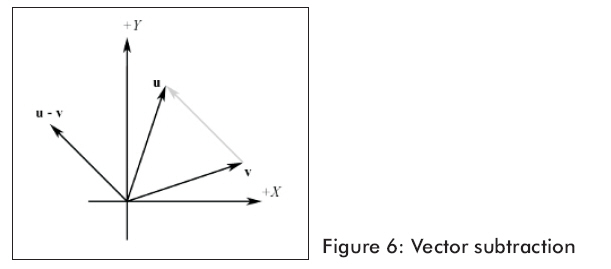
图6显示的是几何学上的向量相减。
两个向量相减的代码,我们使用重载的减法操作符:
|
D3DXVECTOR3 u(2.0f, 0.0f,
1.0f);
D3DXVECTOR3 v(0.0f, -1.0f,
5.0f);
D3DXVECTOR3 difference = u
- v; // = (2.0f, 1.0f, -4.0f)
|
图6显示,向量减法得到一个从v向量终点到u向量终点的向量。假如我们解释u和v的分量,我们能用向量相减找到从一个点到另一个点的向量。这是非常方便的操作,因为我们常常想找到从一个点到另一个点的方向向量。
我们能用一个标量与向量相乘,就象名字暗示的一样,向量按比例变化。这种运算不会改变向量的方向,除非标量是负数,这种情况向量方向相反。