接上一篇我们已经得到了一个完整的ε-NFA,下面来说说如何将ε-NFA转换为DFA(确定有限自动机)。
DFA的状态
在DFA中,某个状态对应到ε-NFA中的若干状态,应此我们将会得到下面这样的一个结构。
struct DFA_State
{
set<EpsilonNFA_State*> content;
bool bFlag;
#ifdef _DEBUG
uint idx;
#endif
DFA_State(const set<EpsilonNFA_State*>& x) : content(x), bFlag(false)
{
#ifdef _DEBUG
idx = inc();
#endif
}
inline const bool operator==(const DFA_State& x)const
{
if (&x == this) return true;
return content == x.content;
}
#ifdef _DEBUG
inline uint inc()
{
static uint i = 0;
return i++;
}
#endif
};
可以看到,为了调试方便我们在结构中定义了状态的唯一ID以及对应到ε-NFA状态的集合和一个标记位。
DFA的边
根据上一篇的经验,不难想到DFA的边应该是什么样的,下面直接给出代码,不做说明。
struct DFA_Edge
{
struct
{
Char_Type char_value;
String_Type string_value;
}data;
enum Edge_Type
{
TUnknown = 0,
TNot = 1,
TChar = 2,
TString = 4
};
uchar edge_type;
DFA_State* pFrom;
DFA_State* pTo;
DFA_Edge(const Char_Type& x, bool bNot, DFA_State* pFrom, DFA_State* pTo) : pFrom(pFrom), pTo(pTo)
{
data.char_value = x;
edge_type = bNot ? (TChar | TNot) : TChar;
}
DFA_Edge(const String_Type& x, bool bNot, DFA_State* pFrom, DFA_State* pTo) : pFrom(pFrom), pTo(pTo)
{
data.string_value = x;
edge_type = bNot ? (TString | TNot) : TString;
}
inline const bool isNot()const
{
return (edge_type & TNot) == TNot;
}
inline const bool isChar()const
{
return (edge_type & TChar) == TChar;
}
inline const bool isString()const
{
return (edge_type & TString) == TString;
}
const Edge_Type edgeType()const
{
if (isChar()) return TChar;
else if (isString()) return TString;
else return TUnknown;
}
const bool operator<(const DFA_Edge& x)const
{
return (ulong)pFrom + pTo < (ulong)x.pFrom + x.pTo;
}
const bool operator==(const DFA_Edge& x)const
{
return pFrom == x.pFrom && pTo == x.pTo;
}
};
由于DFA中不存在ε边,应此DFA将会存在若干个结束状态,但他只有一个开始状态
DFA_State* pDFAStart;
set<DFA_State*> pDFAEnds;
set<DFA_Edge> dfa_Edges;
为了下一步分析的高效,以后可能会将这里的dfa_Edges同样修改为hashmap。
至此DFA所要用到的两个结构迅速的介绍完了。
子集构造算法
通过各种资料,我们不难发现,从ε-NFA转换到DFA的过程中,最常用就是子集构造算法。子集构造算法的主要思想是让DFA的每个状态对应NFA的一个状态集。这个DFA用它的状态去记住NFA在读输入符号后达到的所有状态。(引自编译原理)其算法如下
输入:一个NFA N。
输出:一个接受同样语言的DFA D。
方法:
1.求取ε-NFA初始状态的ε闭包作为DFA的起始状态,并将这个状态加入集合C中,且它是未标记的。同时记录它的向后字符集。
2.从集合C中取出一个未被标记的子集T和其对应的字符集,标记子集T。
3.使用上一步取出的字符集通过状态转移函数求出转移后的状态集M。
4.求取上一步得到的状态集M的ε闭包U
5.如果U不在集合C中则将U作为未被标记的子集加入C中,同时记录它的向后字符集。检查状态U中是否存在NFA中的终结状态,若存在则将状态U加入到pDFAEnds中。
重复2,3,4,5部直至集合C中不存在未被标记的状态。
ε闭包
ε闭包是指从某个状态起只经过ε边达到的其他状态的集合,同时这个状态也属于这个集合中。其算法如下
输入:状态集k。
输出:状态集U和其所对应的向后字符集。
方法:
1.遍历状态集k中的每个状态k'。
2.若k'不存在于结果状态集U中,将k'插入U中。
3.建立一个临时集合tmp,并将k'插入其中。
4.从临时集合tmp中取出一个状态p。
5.取出所有从p出发的边,若这条边是ε边,且抵达状态不在结果状态集U中,将抵达的状态分别插入结果状态集U和临时集合tmp中。若这条边是字符集的边且这条边所对应的字符不在向后字符集中,则将向后字符插入向后字符集中。
6.将状态p从临时集合tmp中删除。
循环4,5,6部直至tmp中不存在任何状态为止。
由于在生成ε-NFA时不存在只有ε边的循环,应此这里不会产生死循环。下面给出具体的代码
void epsilonClosure(const set<EpsilonNFA_State*>& k, EpsilonClosureInfo& info)
{
for (typename set<EpsilonNFA_State*>::const_iterator i = k.begin(), m = k.end(); i != m; ++i)
{
info.states.insert(*i);
set<EpsilonNFA_State*> tmp;
tmp.insert(*i);
while (!tmp.empty())
{
EpsilonNFA_State* pState = *tmp.begin();
for (typename vector<EpsilonNFA_Edge>::const_iterator j = epsilonNFA_Edges[pState].begin(), n = epsilonNFA_Edges[pState].end(); j != n; ++j)
{
if (j->isEpsilon())
{
if (info.states.insert(j->pTo).second) tmp.insert(j->pTo);
}
else if (j->isChar()) info.chars.insert(pair<Char_Type, bool>(j->data.char_value, j->isNot()));
else if (j->isString()) info.strings.insert(pair<String_Type, bool>(j->data.string_value, j->isNot()));
}
tmp.erase(pState);
}
}
}
其中用到的EpsilonClosureInfo结构为
struct EpsilonClosureInfo
{
set<EpsilonNFA_State*> states;
set<pair<Char_Type, bool> > chars;
set<pair<String_Type, bool> > strings;
EpsilonClosureInfo() {}
EpsilonClosureInfo(const set<EpsilonNFA_State*>& states,
const set<pair<Char_Type, bool> >& chars,
const set<pair<String_Type, bool> >& strings)
: states(states)
, chars(chars)
, strings(strings) {}
EpsilonClosureInfo(const EpsilonClosureInfo& x)
{
states = x.states;
chars = x.chars;
strings = x.strings;
}
};
需要保存的是状态集和向后字符集。
状态转移函数
通过状态转移函数,输入一个集合T和一个字符a将可得到所有通过T中的每一个状态和a边所能达到的状态的集合。应此代码如下
set<EpsilonNFA_State*> move(const DFA_State& t, const Char_Type& c, bool bNot)
{
set<EpsilonNFA_State*> result;
for (typename set<EpsilonNFA_State*>::const_iterator i = t.content.begin(), m = t.content.end(); i != m; ++i)
{
for (typename vector<EpsilonNFA_Edge>::const_iterator j = epsilonNFA_Edges[*i].begin(), n = epsilonNFA_Edges[*i].end(); j != n; ++j)
{
if (j->isChar() && j->data.char_value == c && j->isNot() == bNot) result.insert(j->pTo);
}
}
return result;
}
set<EpsilonNFA_State*> move(const DFA_State& t, const String_Type& s, bool bNot)
{
set<EpsilonNFA_State*> result;
for (typename set<EpsilonNFA_State*>::const_iterator i = t.content.begin(), m = t.content.end(); i != m; ++i)
{
for (typename vector<EpsilonNFA_Edge>::const_iterator j = epsilonNFA_Edges[*i].begin(), n = epsilonNFA_Edges[*i].end(); j != n; ++j)
{
if (j->isString() && j->data.string_value == s && j->isNot() == bNot) result.insert(j->pTo);
}
}
return result;
}
为了分别支持Char_Type和String_Type的字符我们定义了两个move函数。
最后我们给出子集构造算法的代码
void buildDFA()
{
set<EpsilonNFA_State*> start;
start.insert(pEpsilonStart);
typedef pair<DFA_State*, EpsilonClosureInfo> c_type;
map<size_t, list<c_type> > c;
queue<c_type> c2;
pDFAStart = DFA_State_Alloc::allocate();
EpsilonClosureInfo info;
epsilonClosure(start, info);
construct(pDFAStart, info.states);
c_type ct(pDFAStart, info);
c[info.states.size()].push_back(ct);
c2.push(ct);
if (isEndDFAStatus(pDFAStart)) pDFAEnds.insert(pDFAStart);
context.dfa_States.insert(pDFAStart);
while (!c2.empty())
{
DFA_State* t = c2.front().first;
set<pair<Char_Type, bool> > chars = c2.front().second.chars;
set<pair<String_Type, bool> > strings = c2.front().second.strings;
t->bFlag = true;
for (typename set<pair<Char_Type, bool> >::const_iterator i = chars.begin(), m = chars.end(); i != m; ++i)
{
EpsilonClosureInfo info;
epsilonClosure(move(*t, i->first, i->second), info);
DFA_State* p = getDFAState(info.states, c);
if (p) // 如果这个状态已存在
{
dfa_Edges.insert(DFA_Edge(i->first, i->second, t, p));
}
else
{
DFA_State* pState = DFA_State_Alloc::allocate();
construct(pState, info.states);
context.dfa_States.insert(pState);
if (isEndDFAStatus(pState)) pDFAEnds.insert(pState);
c_type ct(pState, info);
c[info.states.size()].push_back(ct);
c2.push(ct);
dfa_Edges.insert(DFA_Edge(i->first, i->second, t, pState));
}
}
for (typename set<pair<String_Type, bool> >::const_iterator i = strings.begin(), m = strings.end(); i != m; ++i)
{
EpsilonClosureInfo info;
epsilonClosure(move(*t, i->first, i->second), info);
DFA_State* p = getDFAState(info.states, c);
if (p) // 如果这个状态已存在
{
dfa_Edges.insert(DFA_Edge(i->first, i->second, t, p));
}
else
{
DFA_State* pState = DFA_State_Alloc::allocate();
construct(pState, info.states);
context.dfa_States.insert(pState);
if (isEndDFAStatus(pState)) pDFAEnds.insert(pState);
c_type ct(pState, info);
c[info.states.size()].push_back(ct);
c2.push(ct);
dfa_Edges.insert(DFA_Edge(i->first, i->second, t, pState));
}
}
c2.pop();
}
}
尾声
同样我们来编写一个函数来打印出DFA。
void printDFA()
{
printf("---------- DFA Start ----------\n");
set<DFA_State*> tmp;
for (typename set<DFA_Edge>::const_iterator i = dfa_Edges.begin(), m = dfa_Edges.end(); i != m; ++i)
{
printf("%03d -> %03d", i->pFrom->idx, i->pTo->idx);
switch (i->edgeType())
{
case DFA_Edge::TChar:
printf("(%c)", i->data.char_value);
break;
case DFA_Edge::TString:
printf("(%s)", i->data.string_value.c_str());
break;
default:
break;
}
if (i->isNot()) printf("(not)");
printf("\n");
tmp.insert(i->pFrom);
tmp.insert(i->pTo);
}
printf("start: %03d -> ends: ", pDFAStart->idx);
for (typename set<DFA_State*>::const_iterator i = pDFAEnds.begin(), m = pDFAEnds.end(); i != m; ++i)
{
printf("%03d ", (*i)->idx);
}
printf("\n");
#if DEBUG_LEVEL == 3
printf("-------------------------------\n");
for (typename set<DFA_State*>::const_iterator i = tmp.begin(), m = tmp.end(); i != m; ++i)
{
printf("State: %03d\n", (*i)->idx);
for (typename set<EpsilonNFA_State*>::const_iterator j = (*i)->content.begin(), n = (*i)->content.end(); j != n; ++j)
{
printf("%03d ", (*j)->idx);
}
printf("\n");
}
#endif
printf("----------- DFA End -----------\n");
}
最后我们加入测试代码
Rule_Type::Context context;
Rule_Type a('a', context), b('b', context), d('d', context);
Rule_Type result = (a - d).opt() + (+b | !(a + b));
result.buildDFA();
#ifdef _DEBUG
result.printEpsilonNFA();
result.printDFA();
#endif
可打印出如下内容
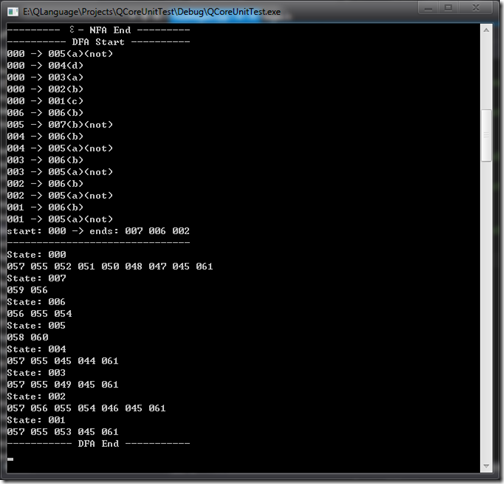
画成图如下
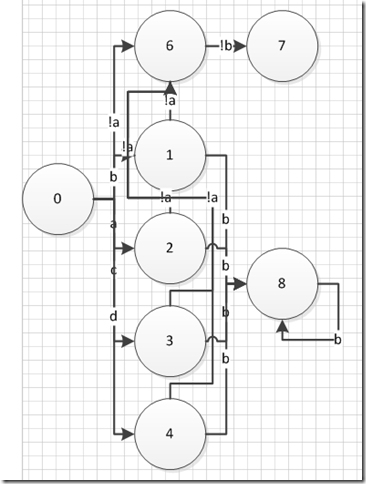
完整的代码可到http://code.google.com/p/qlanguage下载
posted on 2013-02-23 23:30
lwch 阅读(2868)
评论(0) 编辑 收藏 引用 所属分类:
QLanguage