LZ4 (Extremely Fast Compression algorithm)

项目：http://code.google.com/p/lz4/

作者：Yann Collet

本文作者：zhangskd @ csdn blog

简介

LZ4 is a very fast lossless compression algorithm, providing compression speed at 400MB/s per core,

scalable with multi-cores CPU. It also features an extremely fast decoder, with speed in multiple GB/s per core,

typically reaching RAM speed limits on multi-core systems.

A high compression derivative, called LZ4_HC, is also provided. It trades CPU time for compression ratio.

(1) 横向对比

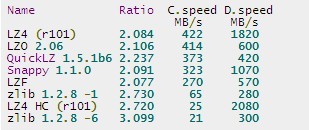
Quick comparison: single thread, Core i5-3340M @2.7GHz, using the Open-Source Benchmark by m^2 (v0.14.2)

compiled with GCC v4.6.1 on Linux Ubuntu 64-bits v11.10, using the Silesia Corpus.

对比当前流行的压缩工具，可以看到LZ4具有最快的压缩和解压速度，尽管压缩比一般。

QuickLZ官网：http://www.quicklz.com/

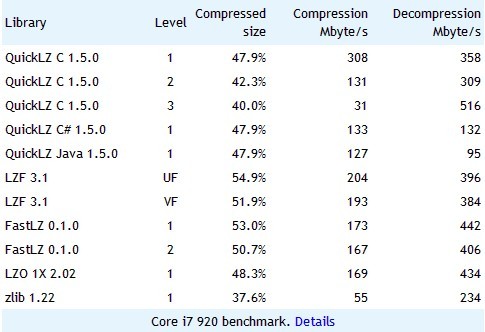
QuickLZ is the world's fastest compression library, reaching 308MB/s per core.

QuickLZ自称是世界上最快的压缩算法，然而我们看到它和LZ4还是有差距的，特别是解压速度。

snappy项目：https://code.google.com/p/snappy/

snappy is developed by Google based on ideas from LZ77 and open-sourced in 2011.

It was designed to be very fast and stable, but not to achieve a high compression ratio.

Compression speed is 250MB/s and decompression speed is 500MB/s using a single threaded,

64-bit core i7 processor. The compression ratio is 20-100% lower than gzip.

snappy追求的是速度，压缩比并不高。

(2) 纵向对比

LZ4能很好的支持多线程环境，获得更高的压缩和解压速度。

(3) 技术背景

多媒体技术 -> 无损压缩 -> 词典编码 -> LZ77算法 -> LZ4

词典编码(Dictionary Encoding)，根据的是数据本身包含有重复代码序列这个特性。

主要分为两类：

1. 查找正在压缩的字符序列是否在前面输入数据中出现过，如果是，则用指向早期出现过的字符串的“指针”替代

    重复的字符串。这里的“词典”是指以前处理过的数据。（LZ77、LZSS）。

2. 从输入的数据中创建一个“短语词典”，编码数据过程中当遇到已经在词典中出现过的“短语”时，编码器就输

    出这个词典中的短语的“索引号”，而不是短语本身。（LZ78、LZW）

(4) 其它格式

以下是一些常用的压缩格式。

1. zip

    zlib库，可通过包含zlib.h使用。

    zip原名为Deflate，仅支持一个LZ77的变种算法Deflate。

    zip/unzip，后缀为.zip。zip也是Windows下常见的压缩格式。

2. gzip

    gzip/gunzip是GNU程序，后缀为.gz。Web也常用GZIP压缩技术。

    首先使用LZ77算法进行压缩，对结果再使用huffman编码进行压缩。

    tar中用-z来调用：

         tar -czf pic.tar.gz *.jpg

         tar -xzf pic.tar.gz

3. bzip2

    bzip2/bunzip2，后缀为.bz2。

    相比于gzip，压缩比更高，压缩效果比传统的LZ77/LZ78更好，但压缩速度较慢。

    首先使用Burrows-Wheeler变换（BWT，块排序文本压缩），然后使用哈夫曼编码进行压缩。

    tar中使用-j来调用：

        tar -cjf pic.tar.bz2 *.jpg

        tar -xjf pic.tar.bz2

4. compress

    compress/uncompress，后缀为.Z，现在已经不再流行了。

    使用LZ78算法的变种LZW。

    tar中使用-Z来调用。

6. rar

    rar/unrar，后缀为.rar。

    rar格式较zip格式的压缩比高。

    注意RAR非免费，是Windows下常见压缩格式，也有RAR for Linux。

        rar a pic *.jpg // pic.rar

        rar e pic.rar // pic

7. 7z

    7-Zip，后缀为.7z。

    和rar、zip一样，7z也是Windows下常见的压缩格式。

    使用改良与优化后的LZ77算法LZMA、LZMA2，压缩比高于zip。

8. xz

    xz，后缀为.xz。

    如果说LZ4是压缩速度之王，xz则是压缩比之王。

    一般来说，用xz压缩后的文件，能比用gzip压缩的小30%，比用bzip2压缩的小15%。

    主要使用LZMA2压缩算法。

    tar不支持xz格式，xz / xz -d。

LZ77

我们看到很多压缩格式都是基于LZ77的，所以先来了解下LZ77算法，这里引用了较多的网上资料：）

1977年，Jacob Ziv和Abraham Lempel描述了一种基于滑动窗口缓存的技术，该缓存用于保存最近刚刚处理的文本。

LZ77编码的核心是查找从前向缓冲器开始的最长的匹配串。

压缩算法使用了两个缓存：

1. 滑动历史缓存，包含了前面处理过的N个源字符。

2. 前向缓存，包含了将要处理的下面L个字符。

压缩过程

算法尝试将前向缓存开始的两个或多个字符与滑动历史缓存中的字符串相匹配。

如果没有发现匹配，前向缓存的第一个字符作为9bit的字符输出并且移入滑动窗口，滑动窗口中最久的字符被移除。

如果找到匹配，算法继续扫描以找到最长的匹配。然后匹配字符串作为三元组输出(选项、指针和长度)。对于K个字符

的字符串，滑动窗口中最久的K个字符被移出，并且被编码的K个字符被移入窗口。

更具体来说：

1. 从当前压缩位置开始，查看未编码的数据，并试图在滑动窗口中找出最长的匹配字符串，如果找到，则进行步骤2，否则进行步骤3。

2. 输出三元符号组(off, len, c)。其中off为窗口中匹配字符串相对窗口边界的偏移，len为可匹配的长度，c为下一个字符。

    然后将窗口向后滑动len + 1个字符，继续步骤1。

3. 输出三元符合组(0, 0, c)。其中c为下一个字符。然后将窗口向后滑动len + 1个字符，继续步骤1。

实例

假设窗口大小为10个字符，我们刚编码过的字符(滑动窗口)是：abcdbbccaa，即将编码的字符(前向缓存)是：abaeaaabaee。

1. 和编码字符匹配的最长串为ab，下一个字符为a，输出三元组(0, 2, a)。

    窗口向后滑动3个字符为：dbbccaaaba，前向缓存为：eaaabaee。

2. 字符e在窗口中无匹配，输出三元组(0, 0, e)，窗口向后滑动1个字符为：bbccaaabae，前向缓存为：aaabaee。

3. 前向缓存的最长匹配串为aaabae，下一个字符为e，输出三元组(4, 6, e)，完成编码。

解压过程

解压算法必须保存解压输出的最后N个字符（滑动窗口）。

当碰到编码字符串时，使用指针和长度字段，将编码替换成实际的正文字符串。

评价

算法使用了有限的窗口在以前的文本中查找匹配，对于相对于窗口大小来说非常长的文本块，很多可能的匹配就会被丢掉。

窗口大小可以增加，但这会带来两个损失：

1. 算法的处理时间会增加，因为它必须为滑动窗口的每个位置进行一次与前向缓存的字符串匹配的工作。

2. 指针字段必须更长，以允许更长的跳转。

在多数情况下，lz77拥有较高的压缩效率。而在待压缩文件中绝大多数是些超长匹配，并且相同的超长匹配高频率地反复

出现时，lzw更具优势。GIF就是采用了lzw算法来压缩背景单一、图形简单的图片。zip是用来压缩通用文件的，这就是它

采用对大多数文件有更高压缩率的lz77算法的原因。

优化

精心设计三元组(off, len, c)中每个分量的表示方法，才能达到较好的效果。

(1) off

off为窗口内的偏移，通常的经验是，偏移接近窗口尾部的情况要多于接近窗口头部的情况，这是因为字符串在与其接近的

位置容易找到匹配串，但对于普通的窗口大小(如4096字节)来说，偏移值基本还是均匀分布的，我们完全可以用固定的位

数来表示它。

(2) len

len为字符串长度，它在大多数时候不会太大，少数情况下才会发生大字符串的匹配。显然可以使用一种变长编码方式来表

示该长度值。要输出变长的编码，该编码必须满足前缀码的条件。Huffman编码可以用于此处，但不是最好的选择。

Golomb编码应用比较广泛，对于较小的数用较短的编码，对较大的数用较大的编码表示。

(3) c

c为前向缓存中的不匹配字符。直接用8个二进制位编码。

(4) 输出格式

LZ77的原始算法采用三元组输出每一个匹配串及其后续字符，即使没有匹配，仍需要输出一个len=0的三元组来表示单个字符。

实验表明，这种方式对于某些特殊情况(例如同一字符不断重复的情形)有着较好的适应能力。

对一般数据，有一种更有效的输出方式。

将每一个输出分成匹配串和单个字符两种类型，并首先输出一个二进制位对其加以区分。例如，输出0表示下面是一个匹配串，

输出1表示下面是一个单个字符。之后，如果要输出的是单个字符，我们直接输出该字符的字节值，需要8个二进制位。

也就是说，输出一个单个的字符共需要9个二进制位。

如果要输出的是匹配串，则输出off和len。off可以用定长编码，也可以用变长前缀码。len用变长前缀码。有时候我们可以对匹配

长度加以限制，例如，限制最少匹配3个字符。因为对于2个字符的匹配串，我们使用匹配串的输出方式不一定比我们直接输出2

个单个字符(共需18位)节省空间。

这种输出方式的优点是：输出单个字符的时候比较节省空间。另外，因为不强求每次都外带一个后续字符，可以适应一些较长

匹配的情况。

(5) 查找匹配串

在滑动窗口中查找最长的匹配串，是LZ77算法中的核心问题，关系着空间和时间复杂度。

golomb

哥伦布编码。主要针对整数进行编码，对较小的数用较短的编码，对较大的数用较大的编码表示。

假设x为要进行编码的整数，当x趋于较小的取值时候，此时的Golomb编码较短，可以有效的节省空间。

压缩算法：

1. 选定参数m，b = 2^m，注意m是要在压缩前指定的。

2. q = <int> ((x - 1) / b)，<int>表示取整。

3. r = x - qb - 1，所以x = qb + r + 1。(注意这个1不用存储，只要默认恢复出来的数据加1即可)

4. 这样要编码的x由两部分组成：

    a. 第一部分由q个1加上一个0组成，表示q。

    b. 第二部分由m个位组成，表示r。

恢复算法：

如果读入1，则继续往后读，直到读入0，此时读入的1的个数就是q。

之后的m位(m事先约定了)为r。

所以可以计算出x = qb + 1 + r = q * 2^m + r + 1。

Reference

[1]. http://fastcompression.blogspot.com/p/lz4.html

[2]. http://jpkc.zust.edu.cn/2007/dmt/course/MMT03_05_1.htm

[3]. http://jpkc.zust.edu.cn/2007/dmt/course/MMT03_05_2.htm

[4]. http://hi.baidu.com/guoliqiang2006/item/127c8f989b494b4ef14215db

[5]. http://blog.chinaunix.net/uid-17240700-id-3347894.html

[6]. http://jpkc.zust.edu.cn/2007/dmt/course/Mmt03_02_2.htm

[7]. http://tukaani.org/xz/