英雄哪里出来

​

新地址：夜深人静写算法（二十三）- 最短路

      枚举

      题意：给定两个二维坐标上的点(x1, y1)、(x2, y2)，坐标范围为[-10⁶, 10⁶]。求从一个点(x1, y1)到(x2, y2)的直线路径上经过的第N个方格的左下角坐标，无解输出no solution。

图1

      题解：首先，如果两个点的x坐标相同或者y坐标相同，则直接无解；否则将(x1, y1)和(x2, y2)一起做相应的平移，使得(x1, y1)和(0, 0)重合，方便计算。

如果x1 < x2，枚举x坐标属于(x1, x2]，对于每个单位为1的区间[x, x+1]容易计算出y方向上有多少个方格，统计出第n个方格；如果x1 > x2，枚举x坐标属于(x2, x1]，用同样的方法进行计算。


151 Construct a triangle

      解析几何

      题意：给定三角形的两条边AB = c、 AC = b 和 一条中线 AM = m 的长度，求一个满足条件的三角形的坐标。

      题解：由于三角形的坐标可以随意取，所以为了简化问题，可以将A点定在坐标原点，B点定在x轴正方向，C则在第一象限或者第二象限；

       假设A在原点(0, 0)

       B在x+轴上，则有B点坐标(c, 0)

       假设C点坐标为(x, y), 中线坐标为 (B + C) / 2，即 ( (x+c)/2, y/2 )

       已知AM距离m 和AC距离b，则有：

            x² + y² = b²                               (1)

            ((x+c)/2)² + (y/2)² = m²             (2)

      合并(1) (2)，则有

            -2cx - c² = b² - 4 * m²               (3)

            x = (4*m² -b² - c²)/2/c;              (4)

            y² = b² - x²;                              (5)

      根据(5)，可以推出 y² = b² - x² = b² - ((4*m² -b² - c²)/2/c ) ² =>[ (b+c) ² - (2m)² ] * [ - (b-c)² + (2m)² ] > 0

            b+c > 2m 并且 2m > fabs(b-c)时y才有解，所以当 2*m > (b+c) 或者2*m < fabs(b-c) 为无解的情况。

       而我们假设C在第一象限或者第二象限，所以y>0，于是(x, y)可通过(4) (5)求得。

图2

152 Making round

      贪心

      题意：给定N(N <= 10000)个数，求每个数在所有数中所占百分比，要求输出的数之和为100，每个数可以进行上下取整。如：给定三个数3 3 3，那么输出为 34 33 33。34为向上取整的结果，33为向下取整的结果。

      题解：

            1）首先求得所有数之和S，将每个数a[i]除上S得到商B[i]和余数M[i]。

            2）如果余数为0表示为整除，不能进行上下取整。如果余数不为0，说明它有 +1 或者 +0 的机会。 （因为题目说可以上取整，也可以下取整）

            3) 记录下所有余数不为零的个数T。

            4）将所有数的商之和Sum{B[i]} 和 余数不为零的数的个数T 相加，如果小于100，则表明必定无解。否则扫描数组，将 X = 100-Sum{B[i]}-T 的值分派给每个不能整除的数即可（每个数只可分派1）。

153 Playing with matches

      博弈

      题意：给定N根火柴(N <= 10⁹)，每次可以从这些火柴中取1,P1,P2,...,Pm (2<=Pi<=9, 0<=m<=8)根，两人分别轮次进行拾取，并且总是按照最优策略去取，最后取完火柴的人为输的人，问当前状态是否是一个必胜状态。

         题解：经典博弈，对于给定状态X：

                   1) 如果按照所有方式取，最后都只能让对手到达必胜状态，那么X为必败状态；

                   2) 如果对于某种取法，可以让对手达到必败状态，那么X为必胜状态；

               3) 显然，0为必胜态，1为必败态，2为必胜态。

      根据以上的性质，可以通过递推，将火柴根数确定的情况下，将所有状态算出来，但是由于N <= 10⁹，数据量太大，但是我们注意到每个Pi很小，最大值也只有9，某些大状态是通过小状态算出来的，所以必然存在循环。

       于是问题就转化成了求一堆序列的循环节，可以先预处理将5000（足够大就行）以内的状态用记忆化搜索算出来，对于每个状态值，用0表示必胜，1表示必败。枚举循环节的长度len，然后检测是否一个合法的循环节。最后N的状态值就是N % len的状态值。

154 Factorial

      二分统计 + 初等数论

       
      题意：给定一个数N，求一个最小的数K，使得K!末尾正好有N个0。

      题解：因为K!中的质因子中5的个数明显比2的个数少，所以求末尾有多少个0，其实就是求K!中有多少个质因子5。那么这些质因子一定出现在 5、10、15、25、30、35、... K中，对于 K!，将所有的5的倍数提出来，剩下部分为T，则有：

      K! = 1*2*3*4*5*...(K-1)*K = 5 * 10 * 15 * ... * (1*2*3*4*6*7*8*9*11*12*13*14*16*...K) = 5*10*15*...* T = 5* (1*2*3...) * T = 5 * T * K'! ， 我们发现5*T中5的质因子个数为T个，K'! 中的5的个数则可以转化成子问题求解，这样就变成了一个递归求解K中质因子为5的个数S的问题，递归方程为 S[ K ] = K/5 + S[K/5] ( K > 0 ) 当K = 0时返回0，即递归出口。

       那么就可以二分枚举一个K，然后通过上面的递归求解K中5这个质因子的个数，然后和N比较，如果找不到一个K，使得它的5质因子的个数为N则无解，否则找一个最小的。

155 Cartesian Tree

      RMQ(or ZigZag)

      题意：给定N(N <= 50000)个整数对(key, a)，要求将他们组织成一棵树二叉树，并且对于树的任意一个结点，满足如下两个性质：

      1) 当前结点的a值大于它父节点的a值(小顶堆的性质)；

      2) 当前结点的key值大于左子树的key值，并且小于右子树的key值(排序二叉树的性质)；

      题目保证所有的key值和a值都不同。

      题解：首先将所有整数对按key值递增排序，这样我们只需要对数组进行切分，如果第t个结点作为根结点，那么[1, t-1]必定是它的左子树集合，[t+1, N]必定是它的右子树集合，这样就能够保证第二个条件，而第一个条件需要满足父节点的a值小于左右子树的a值，所以第t个结点必定是所有数中a值最小的，于是可以规约出一个递归算法，对于当前区间[l, r]，找到区间内a值最小的作为根结点，然后将它左边的区间和右边的区间进行相同的递归运算。初始区间为[1, N]，当[l, r]满足 l > r即为递归出口。求区间最小值可以采用RMQ。总的时间复杂度为排序的时间复杂度O(N log N)。

      RMQ 资料参阅 http://www.cppblog.com/menjitianya/archive/2014/06/26/207420.html

156 Strange Graph

      欧拉回路
      题意：给定一个N(N <= 10000)个点的连通图，这个图满足以下性质：
            1) 每个顶点v的度数都大于等于2；
            2) 如果顶点v的度数等于2，那么它连接的两个顶点不相邻；
            3) 如果顶点v的度数大于2，那么和v相邻的点u满足以下条件之一；
                  a) u的度数等于2；
                  b) 任何和v相邻的点(除了u)中都两两相邻；

      求这个图的一个哈密尔顿回路(经过每个顶点一次的回路)。

题解：首先将所有度数为2的点进行标记，那么从这个图的定义中可知，未标记的点必定是在一个完全子图中的，将图中所有完全子图中的点缩成一个点，对缩完点的图统计度数，如果所有的点的度数都为偶数，那么必定存在一个欧拉回路，求出欧拉回路后再拆点转换成哈密尔顿回路；否则，欧拉回路不存在，哈密尔顿回路也就不存在。

157 Patience

      打表题
      题意：给定N(1 <= N <= 13)，表示(1 2 3 ... N 空)这N+1个位置，其中N个位置随机排放着1-N中的某一张牌，每次可以在“空”左边的位置找到一张牌K，然后将K+1这张牌放在“空”的位置上，问哪些初始状态可以到达一个状态使得前N个格子的牌有序排列（第N+1个位置留空）。
      题解：从(1 2 3 ... N 空)这个状态起，反向模拟，能够到达的状态都是可达状态，统计所有可达状态的个数，N的最大值为13，时间上不允许可以客户端计算出值然后打表！

158 Commuter Train

      二分枚举

      题意：车站长度为L(L <= 5000)，给定N（N<= 300）个乘客在车站的位置，以及一辆公交车的M（M <= 300）个车门离车头的位置，乘客一定会选择离自己最近的车门进入，问这辆车要停在哪里可以使得所有人进入车门需要走的距离总和最大，好变态的想法。

      题解：只要枚举车需要停靠的位置，然后枚举每个人到达的那个车门花费的距离总和，取最大值就是答案。

      这里对于某个人需要去哪个车门可以采用二分枚举，因为车门是有序的，只要二分找到离它最近的左车门，那么下一个就是最近的右车门（需要考虑边界，最左和最右的情况都只有一个车门），然后取左、右车门的距离小者。仔细想一下，最大值不一定出现在整点上，也有可能出现在0.5的位置上，所以可以将所有坐标都乘2，然后最后答案再除二避免精度误差。

159 Self-Replicating Numbers

      深度优先搜索

      题意：求N(N <= 2000)位B进制数中平方的最后几位等于该数本身的数的个数。

      题解：利用dfs从最后面一位digit开始枚举[0, B)，模拟相乘后对应位的余数，如果和该数的枚举那一位不相符则不进行下一步搜索，当枚举到第N位完毕，则将解保存，这里需要注意当N为1的时候，最高位可以为0，否则最高位为0的情况需要去掉（最高位为0说明它不是N位数（N>1））。

       PKU 1961 http://poj.org/problem?id=1961

       题意：给定一个长度为N(N <= 10⁶)的字符串S，求它的所有前缀中能够表示成A^K的前缀，并且要求求出每个前缀对应的K。

       题解：KMP

       利用KMP求出该串的Next数组，然后枚举每个前缀，根据Next数组的定义，对于某个前缀S[1...i]，有S[1...Next[i]] = S[i-Next[i]+1...i]，假设前缀S[1...i]能够表示长A^K的形式，则A = S[Next[i]+1...i]，所以必须满足i能够被i - Next[i] 整除，满足条件后K = i/( i - Next[i])。

B. Corporative Network

       PKU 1962 http://poj.org/problem?id=1962

       题意：给定N(N <= 20000)个点和M(M <= 200000)次操作，每次操作有两种类型：

       I a b   将a的父结点设为b，并且合并距离为 |a-b| mod 1000

       E a    询问a到根结点的合并距离。

题解：并查集

利用路径压缩的思想，用dist[p]表示p和p的父结点的合并距离，每次查询的时候累加p到根结点的合并距离，并且将p到p所在树的根结点R的路径上的所有点的父结点都设为R，然后更新各自的合并距离。

合并操作O(1)，查询操作总复杂度O(N)。

C. Cave Exploration

PKU 1963 http://poj.org/problem?id=1963

题意：给出N(N <= 1000)条水平或者垂直的走廊，再给定走廊上任意一个坐标点作为起点以及方向，按照以下策略走：能够左转就左转，不能则笔直走，不能笔直走就右转，都不能就掉头。这样走最后绕一圈又会回到起点，问哪些走廊是没有经过的，只要有一个点走过就算经过。
      题解：模拟 + 哈希。

将水平线段和竖直线段分开存，分两种情况讨论：

      1、水平线段

对于任意一根水平线段，枚举所有的竖直线段，计算出交点和水平线段的端点，保存下来并且按x坐标递增排序，去掉重复点，利用双向链表将两个相邻点连接起来，由于x和y坐标范围为-32767~32767，而交点数不会超过N²，所以可以采用哈希将二维的点映射到一位数组中。每个点记录水平走廊的编号。

      2、竖直线段

同上操作，不同的是每个点记录竖直走廊的编号。

经过1和2两步操作后，走廊上的关键点已经被离散化了，并且所有点都通过四向链表串接起来，然后只需要从起点开始模拟行走即可，走到一个关键点，将关键点所在的两个走廊编号标记掉，最后统计没有标记的走廊编号就是答案了。

D. City Game

       PKU 1964 http://poj.org/problem?id=1964

       题意：给定一个M*N(M <= 1000，N <= 1000)的01矩阵，求它的一个子矩阵，满足矩阵元素全为1，并且面积最大。

题解：枚举行，对于第i行，以第i行为起点，扫描每一列j，找到第一个不是1的数所在的位置P[j]，令K[j] = P[j] - i，于是问题转化成了一个一维的问题。

L[i] 表示 K [ L[i]+1 ... i] 中的元素都大于等于K[i]，但是L[i]小于K[i]；

R[i] 表示 K [i ... R[i]-1] 中的元素都大于等于K[i],但是R[i]小于K[i]；

Max{  (R[i] - L[i] - 1) * K[i],  1 <= i <= N }就是以当前枚举行为起点的最大矩阵，枚举M次取最大值就是全局的最大子矩阵了。

E. Cube Root

       PKU 1965 http://poj.org/problem?id=1965

       题意：给定一个不超过150个数字的正整数，求它的三次方根，精确到小数点后10位。

       题解：大数模拟

将输入的数X用字符串存储，乘上10³⁰，利用二分求出最大的Y，使得Y³ <= X。然后在Y的后十位前插入一个小数点，输出即可。

F. Cable TV Network

       PKU 1966 http://poj.org/problem?id=1966

       题意：求图的点连通度。给定一个N(N <= 50)个点的图，求去掉至少多少个点能够将它变成一个非连通图。

       题解：搜索 + 剪枝 (或者 最大流)

       枚举每个点去掉或不去掉，总共2⁵⁰种状态，每次去掉点后判断当前图的连通性，一旦破坏了连通，去掉的点数即为答案；如果发现某个点去掉后，剩下点组成的图变成了一个完全图，那么不用继续搜索了，因为当前状态下不可能将剩下的图变成非连通图了；如果去掉的点数超过目前的最优解也直接剪枝。

       好吧...一定是数据弱了-_-||，正解是最大流拆点。

G. Alibaba

       PKU 1967 http://poj.org/problem?id=1967

       题意：给定N(N <= 10⁴)个整数对(P_i, D_i)表示在P_i位置有一个宝物，并且需要在D_i 时间之前取走(给出顺序为P_i递增的顺序)。起始可以任意选择一个位置，往左或者往右取宝物，问是否能够保证每个物品都在D_i时间之前取走(时间和距离关系为1:1)，如果可以，给出取完所有宝物的最少时间。

       题解：搜索 + 剪枝

       首先可以想到的是，起始位置一定是N个宝物所在位置中的其中一个，所以首先可以枚举每个宝物的起始点，比如当前位置为pos，那么在第0秒内，访问过的区间为[pos, pos]，可以选择往左走，也可以选择往右走，那么是不是只要选择某个方向走完，然后再反方向走到底如果能够满足所有点都在截止时间内完成一定是对的呢？答案是否定的，来看一组数据，如图1，起始点只能选择3号位置，并且只能选择往右走，走到4后再折回走到2，然后再折回走到5，以此类推，并且只有这一种路径才能满足所有宝物都在截至时间内取完。

图1

         按照这个思路，进行状态的划分，假设当前已经访问的区间为[L, R]，并且现在的位置处于pos位置(这里pos要么等于L，要么等于R)，所以可以用三维来表示状态DP[s][l][r](l、r表示访问过的区间的左右端点，如果当前位置在l则s = 0，如果当前位置在r，则s=1)，总共状态数目N²，状态转移的时候由大状态推小状态，即DP[s][l][r]一定是由DP[0][l-1][r]、DP[0][l][r+1]、DP[1][l-1][r]、DP[1][l][r+1]这四个状态得出。

       考虑到N比较大，所以把所有状态存储到数组中再利用动态规划进行递推，如果数据量不多的话，可以卡过，但是状态存储需要用滚动数组，否则内存吃不消，也可以采用搜索 + 剪枝，思路是沿用了动态规划的思想，假设当前已经访问的区间为[L, R]，现在的位置处于pos位置(这里pos要么等于L，要么等于R)，并且已经使用了T的时间，无论当前的pos是在左区间端点L上还是在右区间端点R上，他都可以选择走到L-1(L > 1)，或者R+1(R < N)，于是就可以递归求解了，递归出口为L=1，R=N的时候。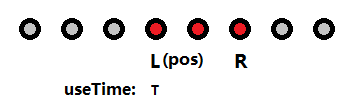

图2

       如图，已经访问的宝物为红色标记的点，灰色标记的为未曾访问过的，并且现在的位置在已经访问区间的左端点L上，已经使用了T的时间，我们需要判断这个状态是否合法，则需要满足以下的几个不等式。

       1、保证右边未访问的都能在截止时间内访问到：

              T + (P[R] - P[L]) +  (P[R+1] - P[R])  < D[R+1]

              T + (P[R] - P[L]) +  (P[R+2] - P[R])  < D[R+2]

              ...

              T + (P[R] - P[L]) +  (P[N] - P[R])  < D[N]

              将这些等式化简，可得：

              T - P[L]  <  D[R+1] - P[R+1]

              T - P[L]  <  D[R+2] - P[R+2]

              ...

              T - P[L]  <  D[N] - P[N]

              再进行进一步化简，得：

              T - P[L]  <  Min{ D[k] - P[k],  R < k <= N }

       2、保证左边未访问的都能在截止时间内访问到：

              同理，可以得出：

              T + P[R]  <  Min{ D[k] + P[k],  1 <= k < R }

       那么，令 POSTM[i] = Min{ D[k] - P[k],  i < k <= N }

                      PREM[i] = Min{ D[k] + P[k],  1 <= k < i }

       这两个数组可以分别通过一次逆序和顺序的线性扫描求出来，用于搜索的时候判断可行性。例如，当T - P[L] >= POSTM[R] 表示在右边未访问的宝物中有至少一个宝物不能在截止时间前被访问到，T + P[R] >= PREM [R]表示在左边未访问的宝物中有至少一个宝物不能在截止时间前被访问到，直接剪枝。

       还需要一个剪枝，就是在当前时间T加上当前状态下预计访问完所有宝物的最小时间已经比之前求出的最小时间大，直接剪枝。

H . Booklets

       PKU 1968 http://poj.org/problem?id=1968

       题意：N(N <= 3000)本小册子需要分配给S个学校，每个学校得到的是N/S的上整本册子或者N/S的下整本册子，每本册子有一个页数，并且规定分配册子的时候按照页数递增来分配，先把上整本册子分完再分下整的，对于每个学校的分书规则，按照输入的顺序进行分配。求问第T个学校分到的第一本册子的页数。

       题解：需要求出几个量：

       上整册子的数目UIP = (N+S-1) / S;

       下整册子的数目LIP = N/S;

       分到上整册子数目的学校个数UIPC = N % S;

       分到下整册子数目的学校个数LIPC = N - N % S;

       首先对所有的册子按页数递增来排序(如果页数相同按照下标递增排序)，然后减去前T-1个学校的册子总数，容易得出第T个学校分到的册子数目C，从接下来的C个册子中找到之前下标最小的册子，它对应的页数就是答案。

I. Count on Canton

       PKU 1969 http://poj.org/problem?id=1969

       题意：给定下图所示的无限分数序列，并且按照蛇形方式编号，即第一个为1/1，第二个为1/2，第三个为2/1，第四个为3/1，以此类推，问第N个分数是什么。

               1/1         1/2         1/3         1/4           1/5 ...

               2/1         2/2         2/3         2/4

               3/1         3/2         3/3

               4/1         4/2

               5/1

    题解：数学题。

    首先二分求出在第几条斜线上，即(K-1)K/2 < N的最大的K，然后求根据K的奇偶性求出蛇形在第K条斜线的行走方向，第N - (K-1)K/2 个数就是答案。

       PKU 1298 http://poj.org/problem?id=1298

         题意：解码题，按照如下对应关系解码：

       密文 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 
       原文 V W X Y Z A B C D E F G H I J K L M N O P Q R S T U 

       题解：简单题。

B. Polar Explorer

PKU 1299 http://poj.org/problem?id=1299

题意：给定圆的半径X，求圆周上两个点A和B的距离，其中圆心角AOB的角度为Z(0 <= Z <= 360)。

题解：核心是Z如果大于180，则Z = 360 - Z，即走劣弧。而且题目求的是来回一次，所以计算的时候弧长要乘2。

C. Door Man

PKU 1300 http://poj.org/problem?id=1300

题意：给定一些边和起点s，求能否找到一条从s到0的通路，并且要求访问所有的边。

题解：欧拉回路可行解判定。

首先利用flood fill从s遍历全图，如果0点没有被访问到则必定不存在；然后判断度数不为0的点是否有未被访问到的，如果有，说明图不连通，也必定不存在解；最后统计度数为奇数的点的个数P，以及具体的点：

1)  P = 0，则必定有解；

2)  P > 2，则无解；

3)  P =2, 那么有解的前提是两个奇度数点中一个是s，另一个是0；否则无解。

D . The Umbrella Problem 2054

PKU 1301 http://poj.org/problem?id=1301

题意：给定一个10X10的地图，玩家从第一行的某一个点出发，每一步行编号+1，列编号增量有三种选择(-1, 0, 1)，图中标记为S(laser gun)的点不能走，并且S的点会发出镭射光，第0秒朝上发射，第1秒朝右，第2秒朝下，第3秒朝左，循环往复，发射长度一直到地图边缘。问能否走到最后一行标记为G(grass)的地方。

题解：广搜。

hash[4][R][C]表示状态，每走一步，利用步数 mod 4计算出镭射光的方向，然后将所有的镭射光可达区域全部标记出来，未标记的点为可达点，枚举三个方向进行搜索。

E. Blue Gene, Jr.

       PKU 1302 http://poj.org/problem?id=1302

       题意：一个长度为N(N <= 20)的病毒基因串A[1...N]进行变异，变异过程从左往右，分情况讨论：

       1) 如果第i个字符是 A-Z，则它将变异成数字n mod 10，n表示A[i+1...N]中变异基因的数目；

       2) 如果第i个字符是 1-9，则它变异成A[i] - 1，并且如果第p (p = i + A[i])个基因存在的话，从第p个基因开始变异；否则从第i+1个基因开始变异；

       题解：题意理解后就是个水题了，递归求解。

F . Byte Me!

       PKU 1303 http://poj.org/problem?id=1303

       题意：二进制二十一点(二进制黑杰克)是由两种牌组成的游戏，一种称为bytes(一个8比特的序列表示0-255之间的数)，一种称为nibbles((一个4比特的序列表示0-15之间的数)，游戏玩法如下：

       1) 游戏的目标是获得尽量接近510分，并且不能超过它；

       2) 每个玩家有两张牌，一张面朝上，一张面朝下(庄家不知道是什么牌)；

       3) 每个玩家有四次叫牌机会，可以叫bytes，也可以叫nibbles，但是如果分数超过510则不能再叫牌；

       4) 所有的叫牌都是面朝上的；

       5) 如果玩家分数超过510，立即判为输；

       5) 庄家最后一个叫牌；

       7) 平局的情况庄家胜(如果所有人都超过510分，庄家还是赢的)；

庄家的规则如下：

       1) 当看到自己和其他人面朝上的牌，判断已经必胜时不要再叫牌了；

       2) 如果总分小于382时 需要叫一次byte牌；

       3) 如果总分小于等于500时 需要叫一次nibble牌；

还有两个隐藏规则：

       1) 你是庄家；

       2) 每个非庄家的玩家面朝下的牌是11111111（但是庄家不知道），面朝上的牌给定；

       3) 非庄家不会叫牌(因为他们比较笨)；

       给定庄家的牌和其他玩家面朝上的牌，以及牌堆中的bytes牌和nibble牌，求庄家的四次叫牌能否获胜；

       题解：题目说了一大堆，最后非庄家的玩家都不会叫牌，o(╯□╰)o...所以只要根据庄家的规则进行叫牌，然后判断是否能够胜出即可；

       因为其他人都不叫牌，每个人都有两张牌，所以其他人的总分不可能超过510分，所以，如果庄家叫牌超过510分直接被判为负。

       每次叫牌前先判断所有玩家的朝上的卡片分数加上255和庄家当前得分进行比较，如果有一个玩家分数大于庄家分数，则庄家按照382和500这两个区间进行叫牌。

       四次叫牌结束，如果所有玩家分数都小于等于庄家分数，则判断庄家分数是否大于510，如果是，输出Bust!，否则输出Win!；如果小于某个玩家的分数，那么输出Lose!。

G . World's Worst Bus Schedule

       PKU 1304 http://poj.org/problem?id=1304

       题意：公交车站有N(N <= 20)辆车，每辆车的发车时间间隔为a1 a2 a3 a4... a1 a2 a3 a4... a1 a2 a3 a4...，循环发车，问某人在T时刻赶到公交车站，最少需要等待多少时间能够乘上公交车。

       题解：对于每辆公交车，设它的所有时间间隔之和为S，令T' = T mod S，然后枚举所有的发车间隔，前i个发车间隔a[i]之和减去T'中的最小正值就是等这辆公交车需要的时间，取所有公交车的最小时间就是所求。

A. Artificial Intelligence?

PKU 2256 http://poj.org/problem?id=2256

题意：功率的计算公式为P = UI，给定一句话，这句话中一定会包含三个变量中的两个，求另外一个，并且单位会有三种前缀m(毫)，k(千)，M(兆)。

题解：字符串扫描。

gets读入字符串，进行一次遍历，查找是否包含子串’P=’, ‘U=’, ‘I=’, 格式化它后面的数字，需要用double来存，然后检查单位前缀，m需要将原值除上103，k需要将原值乘上103，M需要将原值常上106。然后分三种情况计算未知的那个值即可。

B. Balancing Bank Accounts

PKU 2257 http://poj.org/problem?id=2257

题意：给定N(N <= 20)个人，以及M(M <= 1000)条关系，每条关系的描述为nameA nameB C，表示nameA这个人给了nameB这个人C块钱，为了让所有人都不亏，需要再给出至多N-1条关系，使得所有人都收支平衡。

题解：贪心。

首先将所有人分成两堆，from_set表示收入大于支出的人的集合，to_set表示支出大于收入的人的集合，并且记录他们各自的 |收入-支出|，然后对于所有的from_set的人按 |收入-支出| 进行递增排序，枚举每个from_set中的人f，去to_set中找到一个人t，满足f剩余的钱小于等于t亏损的钱，并且t是to_set中亏损最少的人，如果找不到这样的人，那么找到亏损最多的那个人，将f的钱给t，循环往复，直到f的钱给完为止。

当from_set中的所有人将钱全部给了to_set中的人后，to_set中也就没有人亏损了，所有人达到收支平衡。

C. The Settlers of Catan

PKU 2258 http://poj.org/problem?id=2258

题意：给定一个N(N <= 25)个点，M(M <= 25)条边的图，求图的最长路，点允许重复，边不允许重复。

题解：前向星 + dfs。

利用前向星存双向边，以每个点为起点深搜遍历整个图，访问过的边哈希，搜索过程更新最长路即可。

D. Team Queue

PKU 2259 http://poj.org/problem?id=2259

题意：Team Queue是这样一种queue，每个元素都有一个Team。

对于queue的push操作，被push的元素从queue中从头到尾扫描，如果扫到一个元素和它属于同一个Team，那么直接将它插入到这个元素后面；如果没有扫到，直接插到对列尾。

对于queue的pop操作，等同于普通queue的pop操作。

队伍数N小于等于1000。

题解：模拟，开1000个队列。

对于插入操作，每个Team的元素插入到对应的队列中，并且记录当前Team的最早插入时间。O(1)

对于弹出操作，枚举所有Team的队列首元素，从中找时间最早的，然后对那个队列执行弹出操作。O(N)。

E. Error Correction

PKU 2260 http://poj.org/problem?id=2260

题意：给定N*N(N < 100)的01矩阵，问是否所有 行和 和 列和 都是偶数，如果是输出OK，如果不是，是否能够通过改变一个值保证 都是偶数， 都不行输出Corrupt。

题解：扫描。

扫描所有 行和 和 列和，如果正好有其中一行R是奇数，并且其中一列C是奇数，那么改变(R, C)的值就能保证全是偶数，否则要么是OK，要么是Corrupt。

F. France '98

PKU 2261 http://poj.org/problem?id=2261

题意：给定16个国家进行淘汰赛，以及一个16*16的矩阵A，其中A[i][j]表示i号国家打败j号国家的概率，问每个国家取得冠军的概率。

题解：动态规划。

dp[0][i]   表示 1/2决赛 第i个人获胜的概率

dp[1][i]   表示 1/4决赛 第i个人获胜的概率

dp[2][i]   表示 1/8决赛 第i个人获胜的概率

dp[3][i]   表示  总决赛 第i个人获胜的概率 

1) 那么显然dp[0][i] = A[i][i^1]

2) dp[1][i]的概率取决于1/2决赛时第i个人获胜的概率乘上他打败1/4决赛中同组的那两个人的概率；

3) dp[2][i]的概率取决于1/4决赛时第i个人获胜的概率乘上他打败1/8决赛中同组的那四个人的概率；

4) dp[3][i]的概率取决于1/8决赛时第i个人获胜的概率乘上他打败 总决赛中同组的那八个人的概率；

直接递推求解，dp[3][i]就是所求。

G. Goldbach's Conjecture

PKU 2262 http://poj.org/problem?id=2262

题意：将一个数分解成两个奇素数的和。

题解：素数筛选，枚举。

H. Heavy Cargo

PKU 2263 http://poj.org/problem?id=2263

题意：给定一个有向图，边权W(u, v)表示从u到v的最大载重为W(u, v)，在给定s和t，求s到t 的最大可能载重。

题解：二分答案 + 判断连通性。

二分枚举答案T，然后从起点到终点进行连通性判定，如果边权小于T的边不可达，二分的最大值就是答案。

A. Constellations

PKU 3690 http://poj.org/problem?id=3690

题意：给定N*M(N<=1000, M <= 1000)的01矩阵S，再给定T(T <= 100)个P*Q(P <= 50, Q <= 50)的01矩阵，问P*Q的矩阵中有多少个是S的子矩阵。

题解：位压缩 + KMP

由于P <= 50，所以我们可以把所有P*Q的矩阵进行二进制位压缩，将P*Q的矩阵的每一列压缩成一个64位整数，这样P*Q的矩阵就变成了一个长度为Q的整数序列，用同样的方式对N*M的矩阵进行压缩，总共可以产生(N-P+1)个长度为M的整数序列，剩下的就是进行最多(N-P+1)次KMP匹配了。

       KMP相关算法可以参阅：

http://www.cppblog.com/menjitianya/archive/2014/06/20/207354.html

图1 ‘*’代表二进制的1, ’0’代表二进制的0

B. DNA repair

       PKU 3691 http://poj.org/problem?id=3691

       题意：给定N(N <= 50)个长度不超过20的模式串，再给定一个长度为M(M <= 1000)的目标串S，求在目标串S上最少改变多少字符，可以使得它不包含任何的模式串（所有串只有ACGT四种字符）。

       题解：AC自动机 + 动态规划

利用模式串建立trie图，trie图的每个结点(即下文讲到的状态j)维护三个结构，

Node{

              Node *next[4];   // 能够到达的四个状态 的结点指针

              int  id;         // 状态ID，用于到数组下标的映射

              int  val;        // 当前状态是否是一个非法状态 （以某些模式串结尾）

}

用DP[i][j]表示长度为i (i <= 1000)，状态为j(j <= 50*20 + 1)的字符串变成目标串S需要改变的最少字符，设初始状态j = 0，那么DP[0][0] = 0，其他均为无穷大。从长度i到i+1进行状态转移，每次转移枚举共四个字符(A、C、G、T)，如果枚举到的字符和S对应位置相同则改变值T=1，否则T=0；那么有状态转移方程 DP[i][j] = Min{ DP[i-1][ fromstate ] + T, fromstate为所有能够到达j的状态 };最后DP[n][j]中的最小值就是答案。

C. Kindergarten

       PKU 3692 http://poj.org/problem?id=3692

       题意：给定G(G <= 200)个女孩和B(B <= 200)个男孩，以及M(0 <= M <= G*B)条记录(x, y)表示x号女孩和y号男孩互相认识。并且所有的女孩互相认识，所有的男孩互相认识，求找到最大的一个集合使得所有人都认识。

题解：二分图最大匹配

一个点集中所有人都认识表示这个点集是个完全图，该问题就是求原图的一个最大团(最大完全子图)，可以转化为求补图的最大独立集，而补图恰好是个二分图。二分图的最大独立集 = 总点数 - 二分图的最大匹配。于是问题就转化成了求补图的最大匹配了。

D. Maximum repetition substring

PKU 3693 http://poj.org/problem?id=3693

题意：给定长度为N(N <= 10⁵)的字符串S，求它的一个最多重复子串(注意：最多重复子串不等于最长重复子串，即ababab和aaaa应该取后者)。

题解：后缀数组 + RMQ

枚举重复子串的长度L，如果对于某个i，有S[i*L ... N]和S[(i+1)*L ... N]的最长公共前缀大于等于L(这一步可以利用后缀数组求解height数组，然后通过RMQ查询区间最小值来完成)，那么以i*L为首，长度为L的子串至少会重复两次。

图2

如图，L=3，i=3的情况，S[3...10]和S[6...10]的最长公共前缀为3，即S[3...5]和S[6...8]完全匹配，所以S[3...5]重复了两次。反之，如果最长公共前缀小于L，必定不会重复（因为两个子串之间出现了断层）。

推广到更一般的情况，如果S[i*L ... N]和S[(i+1)*L ... N]的最长公共前缀为T，那么以S[i*L]为首的重复子串的重复次数为T / L + 1，而且我们可以发现如果以S[i*L]为首，长度为L的子串的重复次数大于等于2，那么它一定不会比以S[(i+1)*L]为首的子串的重复次数少，这个是显然的，比如L为2的时候，ababab一定比abab多重复一次，基于这个性质，我们定义一个new_flag标记，表示是否需要计算接下来匹配到的串(如ababab和abab的情况，前者计算过了，就把new_flag置为false，就不会计算abab的情况了)，得出完整算法：

1) 枚举重复子串的长度L，初始化new_flag标记为true；

2) 枚举i，计算S[i*L ... N]和S[(i+1)*L ... N]的最长公共前缀T；

a) 如果T < L，new_flag标记为true；

b) 如果T >= L，判断new_flag是不是为false，如果为false，说明以S[i*L]为首的串和S[(i-1)*L]为首的串的最长公共前缀大于等于T，跳转到2)；否则转3)；

3) 因为S[i*L, (i+1)*L]有重复子串，但是字典序不一定最小，所以还需要枚举区间 [i-L+1, i+L]，看是否存在字典序更小的子串，比较字典序这一步可以直接使用后缀数组计算出来的rank值进行比较。

       RMQ相关算法可以参阅：

       http://www.cppblog.com/menjitianya/archive/2014/06/26/207420.html

E. Network

       PKU 3694 http://poj.org/problem?id=3694

题意：给定N(N <= 10⁵)个点和M(N-1 <= M <= 2*10⁵)条边的无向连通图，进行Q(Q <= 1000)次加边，每次加入一条边要求输出当前图中有多少条割边。

       题解：无向图割边、最近公共祖先

利用tarjan求出原图的割边，由于这题数据量比较大，所以用递归可能会爆栈，需要栈模拟实现递归过程，tarjan计算的时候用parent[u]保存u的父结点，每个结点进出栈各一次，出栈时表示以它为根结点的子树访问完毕，然后判断(u, parent[u])是否为割边。每次询问u, v加入后会有多少割边，其实就是求u和v的到它们的最近公共祖先lca(u, v)的路径上有多少割边，由于在进行tarjan计算的时候保存了每个结点的最早访问时间dfn[u]，那么有这么一个性质：dfn[ parent[u] ] < dfn[u]，这是显然的(父结点的访问先于子结点)。于是当dfn[u] < dfn[v]，将parent[v]赋值给v，反之，将parent[u]赋值给u，因为是一棵树，所以进过反复迭代，一定可以出现u == v 的情况，这时候的u就是原先u和v的最近公共祖先，在迭代的时候判断路径上是否存在割边，路径上的割边经过(u, v)这条边的加入都将成为非割边，用一个变量保存割边数目，输出即可。

图3

       如图3，图中实线表示树边，虚线表示原图中的边，但是进行tarjan计算的时候7这个结点被(6, 7)这条边“捷足先登”了，于是(4, 7)成为了一条冗余边，计算完后这个图的割边为(1, 2)、(1,3)、(3, 4)、(3, 5)，分别标记bridge[2]、bridge[3]、bridge[4]、bridge[5]为true。

当插入一条边(7, 5)，那么沿着7的祖先路径和5的祖先路径最后找到的最近公共祖先为3(路径为7 -> 6 -> 4 -> 3 和 5 -> 3)，(3, 4)、(3, 5)这两条割边因为加入了(7, 5)这条边而变成了普通边，将标记bridge[4]、bridge[5]置为false。

F. Rectangles

       PKU 3695 http://poj.org/problem?id=3695

       题意：给定N(N <= 20)个矩形，以及M(M <= 10⁵)次询问，询问R(R <= N)个矩形的并。

       题解：离散化 + 暴力( 或 容斥原理 )

       离散化：由于矩形很少，所以可以将它们的XY坐标分别离散到整点，两个维度分别离散，点的总数不会超过2N，对于本次询问，利用前一次询问的结果进行面积的增减，对每个矩形进行判断，一共有两种情况：

1）这个矩形前一次询问出现，本次询问不出现，对它的所有离散块进行自减操作，如果某个离散块计数减为0，则总面积减去这个离散块的面积；

2）这个矩形前一次询问没出现，本次询问出现，对它的所有离散块进行自增操作，如果某个离散块计数累加后为1，则总面积加上这个离散块的面积；

       容斥原理：对于每个询问，利用dfs枚举每个矩形取或不取，取出来的所有矩形作相交操作，所有[奇数个矩形交]的面积和 – 所有[偶数个矩形交]的面积和 就是答案，因为是dfs枚举，所以在枚举到某次相交矩形面积为0的时候就不需要再枚举下去了，算是一个比较强的剪枝。

       如图4，红色区域为被覆盖了一次的区域，橙色区域为被覆盖了两次的区域，黄色区域为被覆盖了三次的区域，那么先将所有的三个矩形加起来，然后需要减掉重叠的部分，重叠的减掉后发现，重叠的部分多减了，即图中黄色的部分被多减了一次，需要加回来。所以容斥原理可以概括为：奇数加，偶数减。

图4

G. The Luckiest number

PKU 3696 http://poj.org/problem?id=3696

题意：给定L(L <= 2*10⁹)，求一个最小的数T，满足T仅由数字’8’组成，并且T是L的倍数。

题解：欧拉定理

首先，长度为N的仅由8组成的数字可以表示为8*(10^N-1)/9。

如果它能被L整除，则可以列出等式(1)：

8*(10^N-1)/9 = KL     (其中K为任意正整数)  (1)

将等式稍作变形得到等式(2)：

(10^N-1) = 9KL/8                            (2)

由于存在分母，所以我们需要先对分数部分进行约分，得到等式(3)：

令A = L/GCD(8, L),  B = 8/GCD(8, L)

(10^N-1) = 9K*A / B                          (3)

因为A和B已经互质，所以如果B不为1，为了保证等式右边仍为整数，K必须能被B整除，而K为任意整数，所以一定能够找到一个K正好是B的倍数，所以可以在等式两边同时模9A，得到(10^N-1) mod (9A) = 0，稍作变形，得到等式(4):

                         (4)       

于是需要引入一个定理，即欧拉定理。

欧拉定理的描述为：若n, a为正整数，且n, a互质，则：

图5

(ψ(n)表示n的欧拉函数，即小于等于n并且和n互素的数的个数)

这样一来，我们发现只要10和9A互质，只需要求9A的欧拉函数，但是求出来的欧拉函数是不是一定使得N最小呢，并不是，所以还需要枚举欧拉函数的因子，如果它的某个因子T也满足(4)的等式，那么T肯定不会比ψ(9A)大，所以T一定更优。

这里9A有可能超过32位整数，所以计算过程中遇到的乘法操作不能直接相乘(两个超过32位整数的数相乘会超过64位整数)，需要用到二分乘法，即利用二进制加法模拟乘法，思想很简单，就直接给出一段代码吧。

H. USTC campus network

PKU 3697 http://poj.org/problem?id=3697

题意：给定N, M(N <= 10⁴, M <= 10⁶)，求N个点的完全图删掉M条边后，和1这个结点相邻的点的数目。

题解：BFS

利用前向星存边(这里边的含义是反的，i和j有边表示i和j不直接连通)。然后从1开始广搜，将和1有边的点hash掉，然后枚举hash数组中没有hash掉的点(这些点是和1连通的)，如果点没有被访问过，标记已访问，入队；然后不断弹出队列首元素进行相同的处理。

这里可以加入一个小优化，将所有点分组，编号0-9的分为一组，10-19的分为一组，20-29的分为一组，然后用一个计数器来记录每个组中的点是否被访问，每次访问到一个点的时候计数器自增，当某个组的计数器为10的时候表示这个组内所有点都被访问过了，不需要再进行枚举了，这样可以把最坏复杂度控制在 O( N*N/10 ) 以下。

KMP

        KMP算法可以说所有数据结构书上都有，上大学的时候也陆陆续续学过三次，每次学完看似理解了，可是过了不到半年又忘记了，或许是因为代码太短，能写出来就以为自己会了，没有深入去理解，导致下次再来看的时候感觉很陌生，一定是这样的。

    今天看了matrix67对KMP的解释，很赞，附上地址：http://www.matrix67.com/blog/archives/115

    为了让老年的自己不用在迟暮的时候再学一遍KMP，还是决定把一些关键性的东西记录下来，如果那时候的自己看到自己当年写的这篇笔记能有恍然大悟的感觉，那么现在就不是在浪费时间了。

      定义：

          S[1... n]   目标串                           T[1...m]   模式串

      算法目的：

          从目标串S中找到一个子串和模式串T完全匹配。

      算法核心思想：

               1) 枚举i从1到n，在S[i-j...i-1]和T[1...j]完全匹配的前提下，判断S[i]是否和T[j+1]相等：

                        a) 如果相等，说明S[i-j...i]和T[1...j+1]完全匹配，那么i和j都自增1；

                        b) 如果不相等，则需要找到一个最大的j' < j，满足S[i-j'...i-1]和T[1...j']完全匹配；

               2) 当i=n或j=m的时候说明匹配结束，否则重复1)；

      对于j'可以这样理解，由于前提是S[i-j...i-1]和T[1...j]完全匹配，如果要找到一个j'满足S[i-j'...i-1]和T[1...j']也完全匹配，那么T[1...j']必定为T[1...j]的后缀，证明如下：首先将以下的子串进行编号： A = S[i-j...i-1]     B = T[1...j]      C = S[i-j'...i-1]     D = T[1...j']

      因为A和B完全匹配，C和D完全匹配，由于C为A的后缀，所以D为B的后缀。

      当S[i]和T[j+1]不相等的时候需要调整j的值，调整完后的j = Next[j](这个Next[j]就是之前所说的j')，需要满足 T[1 ... Next[j] ] = = T[ j - Next[j] + 1... j ]， 并且Next[j]的值最大，比较书面的说法就是Next[j]表示在模式串T中以第j个元素为结尾的最长后缀中满足它是T的前缀的后缀的长度。

      举个例子，T = "ababaaba"的Next数组为 [0, 0, 1, 2, 3, 1, 2, 3]。

      由于Next数组表示的含义只和自身的性质有关，所以在没有目标串的情况下同样可以求出Next数组，KMP的精妙之处就在于求这个Next数组了。

      在上文中提到的S和T的匹配中，每次S[i-j...i-1]都是尽量找到最大的j使得它和T[1...j]完全匹配，当然有可能找不到这样的j，此时令j = 0，即 S[i,i-1]和T[1,0]匹配(这是两个空串，空串和空串也可以匹配，hohoho~~所以j是一定存在的)。如果现在把S换成T，那么问题就转化成了T[i-j...i-1]和T[1...j]的匹配问题了，如果T[i-j...i-1]和T[1...j]完全匹配，并且T[1...j]是和T[i-j...i-1]匹配的最长的串，那么 Next[i-1] 就是 j（思考一下红色字的定义就明白了），于是问题就转化成了T的自我匹配的过程了。
      算法复杂度：
            O(n+m)

    Next函数的求解非常简洁：

 1 #define MAXN 1000010
 2 int next[MAXN];
 3  
 4 // 传入的字符串下标需要以1开头
 5 void getNext(int m, char *str) {
 6 next[1] = 0;
 7 // 枚举模式串的每个位置，判断以当前字符结尾能够匹配到的最大前缀
 8 for(int j = 0, i = 2; i <= m; i++) {
 9     // 在str[i-j i-1]和str[1j] 完全匹配的前提下判断str[i]和str[j+1]是否相等
10     // 如果不相等，则减小j的值，直到匹配到完全相等位置
11         while( j > 0 && str[i] != str[j+1] ) j = next[j];
12         // 如果能够找到以i结尾的后缀和以j+1结尾的前缀完全匹配，j自增1。
13         if(str[i] == str[j+1]) j ++;
14         // 这里j有两种情况：
15         // j = 0    以i结尾的后缀找不到一个前缀和它完全匹配
16         // j > 0    以i结尾的后缀和以j结尾的前缀完全匹配，更新Next函数的值
17         next[i] = j;
18     } 
19 }

PKU 3461 Oulipo

题意：求一个匹配串T在目标串S中的出现次数。

题解：求出T的Next数组，然后和S进行KMP匹配，匹配时当j = =m的时候表示找到一个可行解，计数器+1，然后将Next[j]赋值给j，使得它的最长前缀能够继续和目标串进行匹配。

KMP匹配过程和Next数组的求解是一样的。

 1 // S[1n] 目标串
 2 // T[1m] 匹配串 
 3 int KMP(int n, char *S, int m, char *T) {
 4     int cnt = 0;
 5     for(int j = 0, i = 1; i <= n; i++) {
 6         while( j>0 && S[i] != T[j+1]) j = next[j];
 7         if(S[i] == T[j+1]) j++;
 8         if(j == m) {
 9             cnt ++;
10             j = next[j];
11         }
12     }
13     return cnt;
14 }

HDU 4763 Theme Section

题意：给定一个长度为N(1 <= N <= 106)的字符串S，问能否和模式串EAEBE进行匹配其中A和B表示任意随机字符，如果能匹配，输出E的最大可能长度，不能匹配输出0。

题解：首先利用KMP求出S的Next数组，那么S[1...Next[N]]、S[1...Next[Next[N]]]、S[1...Next[...[N]] ]必定能和S的后缀进行完全匹配，将这些Next[i]利用一次迭代求出来，最终的答案一定在这些值中，然后从大到小枚举这些值，判断可行性。

假设当前枚举长度为i，那么在S[i+1 ... N-i] 中如果能够找到一个长度为i的子串满足和S[1...i]完全匹配，那么i就是一个可行解，又因为枚举是从大到小进行的，所以i就是E可能的最大长度。

于是问题就转变成了判断S[i+1 ... N-i]中是否存在一个和S[1...i]完全匹配的子串。如果存在，那么必定存在一个k( 2*i <= k <= N-i )，使得S[k-i+1 ... k] = = S[1 ... i ]，所以必定有Next[Next[...[k]]] = = i，所以我们可以预先将S[i+1 ... N-i]区间内所有的Next值退化后进行Hash，然后在枚举某个长度i的时候去Hash数组中找i是否被标记，如果被标记说明存在某个k满足S[k-i+1 ... k] = = S[1 ... i ]，i就是最大可能长度。

HDU 2594 Simpsons’ Hidden Talents

题意：给定两个长度不大于50000的串，求两个串的一个最长公共子串满足子串为第一个串的前缀，并且为第二个串的后缀。

题解：将两个串用一个从未出现过的字符连接，拼成一个长度为N的串，然后进行一次自我匹配，求出next数组，根据Next数组的定义，Next[N]就是所求的最大长度。

HDU 3746 Cyclic Nacklace

题意：给定一个长度为N(N <= 105)的字符串S，求在它的末尾添加几个字符使得他变成一个至少重复两次的连续重复串，要求添加的字符数最少。

题解：首先利用KMP进行一次自我匹配求出Next数组，然后枚举重复串的长度i，令x = i * (N/i)，如果x - Next[x] == i，说明S[x]是S的一个连续重复子串（或者叫连续重复前缀更加贴切），理由很简单，将字符串S[x]以长度i为单位分组，

S[1...i]   S[i+1...2i]  S[2i+1...3i]   ……   S[(N/i-1)i + 1...(N/i)i]

   S[1...i]   S[i+1...2i]   ……  S[(N/i-2)i + 1...(N/i-1)i]

由于x + i = = Next[x]，可以列出连等式，有如下等价关系：S[1...i] = = S[i+1...2i] = = ... = = S[(N/i-1)i + 1...(N/i)i]。

那么剩下的就是要看S[x+1...N]是否为S的前缀，同样可以根据Next数组的定义进行判断，特殊的，当x == N时，S[x+1...N] == S[N+1,N]为空串，必定为S的前缀，也是满足条件的，枚举所有满足条件的长度L，取L - (N-x)的最小者就是答案了。

PKU 2406 Power Strings

题意：给定一个长度不超过N(N <= 106)的字符串，它一定是某个串重复K次得到，求这个K的最大值。

题解：假设子串T重复K次后得到串S，那么T的长度一定为L = N/K(要整除)，则T = S[1...L]，将S拆分成K份，每份长度为L，则有

S[1...L] = S[L+1...2L] = S[2L+1...3L] = ... = S[(K-1)L+1...KL]

由于要保证K最大，势必L要取最小，所以根据Next函数的定义，有Next[KL] = (K-1)L;

即Next[N] = N - L，所以L = N - Next[N];

但是得出的长度L还要保证能被N整除，所以如果不能整除说明L = N，即K = 1；而如果能整除，那么K = N / (N - Next[N]);

PKU 2752 Seek the Name, Seek the Fame

题意：给定一个长度为N(N <= 400000)的字符串，求它的前缀等于后缀的所有子串的长度。

题解：考察Next数组的定义。不断迭代求N的Next，Next[N]的Next......然后逆序输出即可。

HDU 3374 String Problem

题意：给定一个长度为N(N <= 106)的字符串S，然后将它进行左移，总共产生N个循环字符串，求其中字典序最小的串的编号以及这样的串的个数，和字典序最大的串的编号以及这样的串的个数。

题解：先求字典序最小的，字典序最大的只需要将每个字符用127减去本身再求一次字典序最小即可；定义两个指针i，j，i初始为0，j初始为1，再定义一个长度变量k = 0：

1) 比较S[i+k] 和S[j+k]的大小关系：

a) 如果相等，k自增1；当k==N则跳出循环，否则继续1)的比较；

b) 如果S[i+k] < S[j+k]，j += k + 1, k = 0; 

c) 如果S[i+k] > S[j+k], i += k + 1, k = 0;

2) 如果i 和j相等，j自增1；当j==N或i==N则跳出循环，否则继续1)的比较；

这样循环结束后如果，取i和j的小者就是答案。

然后在利用求出来的下标，生成一个新的字符串作为匹配串和一个原串的两倍的串作为目标串进行KMP匹配，得到种数。

题意：给定N*M(N<=1000, M <= 1000)的01矩阵S，再给定T(T <= 100)个P*Q(P <= 50, Q <= 50)的01矩阵，问P*Q的矩阵中有多少个是S的子矩阵。

题解：由于P <= 50，所以我们可以把所有P*Q的矩阵进行二进制位压缩，将P*Q的矩阵的每一列压缩成一个64位整数，这样P*Q的矩阵就变成了一个长度为Q的整数序列T，用同样的方式对N*M的矩阵进行压缩，总共可以产生(N-P+1)个长度为M的整数序列，剩下的就是进行最多(N-P+1)次KMP匹配了。

       计算几何：射线旋转

       题意：需要求一个正多边形的N个点，但是给出的只有N和某两个点的坐标。

       题解：核心思想是根据给定的那两个点的坐标确定多边形中心点的坐标，这样边长也确定了，然后利用中心点到其中一个点的射线的旋转求出所有的点坐标。

       1) 正多边形的中心点一定在任意两个顶点的连线的中垂线上，然后根据已知点的相对关系，算出他们和中心点的夹角，利用这两个条件就可以求出中心点的坐标了。

       2) 然后就是要求某个点绕中心点旋转360/N度后的坐标了，做N-1次旋转操作就能求出所有的顶点了。旋转可以通过解方程求解：

       令原单位向量I，旋转alpha角度后的单位向量I_a，其中I和alpha已知，I_x是我们需要求的。那么有以下两个方程：

       1) I.x * I_a.x + I.y * I_a.y = cos( alpha )

       2) I_a.x² + I_a.y² = 1

       将1)中的I_a.x用I_a.y表示代入方程2)，利用一元二次求根公式可以求得两个解，然后算出I_a.x，但是解肯定只有一个，可以用叉乘关系排除掉另外一个解。

121 Bridges painting

      图论：DFS构造

题意：对于一个图，给定它的边和点，现在要求给边染色（黑色或者白色）。问能不能构造一种染色方法，使得所有的度数大于1的点的边都能有至少有一条边为黑色、至少有一条边为白色。

题解：首先考虑什么情况下是不可能染色成功的；如图1所示，对于下面这个图，每个点的顶点度数为2，所以从任意一条边开始染色，相邻边必然为相反色，由于存在奇环，导致必然有一个点的两条边的颜色相同，染色失败。

然后再来考虑怎么将这个图挽救回来，其实这个图失败的点只有一个，如果在那个点上再加一条边，那么整个图貌似就可以认为染色成功了。

于是我们进一步考虑是不是度数为奇数的点造就了这一切：

度数 = 1，该点所在边可以随便染色；

度数 > 1，说明必然存在环；

如果是偶数环，那么经过一系列的交错染色，最后必然能够在该结点上收获两条颜色不一样的边；

如果是奇数环，在染色完毕后，必然还有一条边未被染色（因为度数为奇数），可以大胆的将它染成不同的颜色；

所以对于度数为奇数的点，采用交错染色，一定可以将图染色成功；

如图，可以对于所有奇度数顶点作为根进行一次dfs，按照编号顺序进行深度优先遍历，先遍历到的是1号，标记为黑色，然后将它的第一个儿子标记为白色，遍历完毕，将第二个儿子标记为黑色（交错染色），即每次更换结点的时候就将颜色取反，当我们遍历到边6的时候发现7是一条后向边，于是回到了根结点，完成遍历。

利用同样方法，将所有度数为奇数的点进行一次遍历，然后再将度数为偶数的点进行相同的遍历（因为可能这不是一个连通图，所以如果度数为偶数的点所在的图集合中有奇数环，如图1的情况，那么必然无解）。

遍历完毕，需要对每个点判断是否存在不合法的顶点（边数大于1，并且只有一种染色），如果合法，说明所有边都被染色了，输出解即可。

图1

图2

122 The book

      哈密尔顿回路问题：Ore定理 + 构造

题意：给定N(N <= 1000)个点连成的图，每个点度数大于等于(N+1)/2，求这个图的一条哈密尔顿回路。

题解：

1）首先假设已经得到了一个环R（R的顶点个数为r），那么在未选到环内的点集R’中必然能够找到某个点k和环R中其中一个点j有边相连，假设没有边相连，那么环R和环外的点集R’互不连通，为两个连通分量，和题意相左（因为每个点的度数大于等于（N+1）/2，图论书上有证明，这肯定是一个连通图，故不再累述），故R’中必然存在至少一个点k和R中点j相连，于是将那个点j连接到k上，这样就变成了一个长度为r+1的链。

2）这个链的头为s，尾为k，长度为r+1，不断在剩下的点集中找点连接到s和k上，并且不断更新s和k（连接到头上，连接的点就变成了s，连接到尾上，连接的点就变成了k），直到找到一个极大连通子链（不能再在剩下的点中找到点连接到链的两端了）。

3）由于k和剩下点集R’没有点相连，所以我们只能在这条长链上找和k相连的点t（因为一定可以找到，为什么呢？k本身不就有个链内的点连着嘛，不然它就是个孤立点了）。所以找到(k , t)相连，并且(s, t+1) 相连，然后删掉(t, t+1)这条边，就能够得到一个新的环了，如果此时环的长度为n就结束了，否则继续1）。

 

图3

123 The sum

      递推

       题意：求斐波那契数列的第N(N <= 40)项。

       题解：__int64数组预处理即可。

124 Broken line

      计算几何: 线段判交

       题意：在平面上有一些闭合线段（没有自交和相互交叉），判断给定的点P是否在这个闭合线段内。

       题解：其实就是判断一个点是否在多边形内；

       首先，虚拟出一个无穷远的点Q，然后用PQ和每个闭合线段去做相交检测(两线段判交在黑书上有详尽的解释,不再累述)。

       1) 如果P在某条线段上，输出BORDER；

       2) 如果PQ和所有线段交点个数为奇数，说明在多边形内，输出INSIDE；

       3) 如果PQ和所有线段交点个数为偶数，说明在多边形外，输出OUTSIDE；

 

125 Shtirlits

      深度优先搜索 + 剪枝

       题意：给定一个矩阵B (3X3)，B[i][j]表示A[i][j]四周比它大的数的个数，求满足条件的A。

       题解：枚举A[i][j]的每个数字，数字的范围为 [0,9]。复杂度10⁹，所以需要进行一定的剪枝。

       a)   首先，可以肯定这B[i][j]中一定会至少有一个0，因为总有一个数没有比它大的数（高处不胜寒啊~~）。对于B[i][j] == 0的格子，将A[i][j]设为最大值9一定不会错，所以复杂度至少可以降到 10⁸ 了。

       b)   将A的每个非9的格子标记为-1，然后对每个格子进行枚举，枚举范围为 [ 0, 8 ], 因为B[i][j]为四周比它大的数的个数, 如果A[i][j]==9，那么B[i][j]必须为0，复杂度降至 9⁸。

       c)   每次枚举完毕，进入下一个数的枚举之前，进行全局的检测，对于每个格子统计以下数据：

            i)    已经枚举的邻居格子      H

            ii)   总共有多少个邻居格子   T

             iii)   比自己大的邻居格子       B

     然后进行筛选，如果

          x) 比当前格子大的邻居数已经超出限定值, 即 B > B[i][j]

          y) 比当前格子大的邻居数 + 剩余未知邻居数 < 给定比它大的邻居数， 即 B + (T-H) < B[i][j]

     均为无效解，无需往下枚举，回溯。

       d)   直到所有数枚举完毕，输出解即可。

126 Boxes

      初等数论

       题意：对于给定的A和B，

              如果A > B, 则状态变为 (A-B, 2*B)

              如果A < B, 则状态变为 (2*A, B-A)

              当 A == B 时，结束。

              要求输出这个情况是否存在，如果存在输出变换的次数，不存在输出-1。

       题解：根据题意，可以得出一些简单的推论：

          a) 当A == 0 或者 B == 0 时 答案为 0。

          b) 最后A == B的时候，必定是K = (A+B)/2，所以当A+B为奇数时答案不存在。

          c) 定义最后的状态二元组为 (K, K),

                倒数第二次的操作必定为 (3K/2,K/2)  或者(K/2,3K/2)                                                                                                 (2种)

                倒数第三次的操作必定为 (7K/4, K/4) 或者 (3K/4, 5K/4) 或者 (5K/4, 3K/4) 或者 (K/4, 7K/4)                                         (4种)

                倒数第四次操作(15K/8,K/8)...                                                                                                                                   (8种)

                倒数第i次操作 ( (2^(i-1)-1)/2^(i-1) * K, 1/2^(i-1) * K ) ...                                                                                                    (2^(i-1) 种)

          d) A和B的组合必定在这些情况中找。

              于是定义 A = L1 / 2ⁿ * K,  B = L2 / 2ⁿ * K  (其中K = (A+B)/2, L1,L2为奇数，并且(L1+L2) = 2⁽ⁿ⁺¹⁾)

             得：

                 L1 = 2ⁿ * (A/K)

                 L2 = 2ⁿ * (B/K)

        令 A = 2^a * A', K = 2^k * K'

        则有 L1 = 2^(n+a-k) * A'/K' 为奇数，所以n+a-k = 0，并且要保证A' mod K' == 0，A 和 K 都为已知，则可以计算出 a 、A'、k、K'，最终的步数就是k-a+1。

        需要注意特殊情况：A或B为0的情况，以及A+B为奇数的情况。

127 Telephone directory

      将所有电话号码按首字母排序，统计每个首字母出现的次数Ai， Sum{ (Ai + K - 1 ) / K } + 2 就是答案。

128 Snake

       想法题

       题意：给定N（4<=N<=10000）个整数点，问能不能组出一个多边形，满足以下条件：

       a) 闭合；

       b) 所有的点都是多边形上的点，并且只能被用一次；

       c) 任何两个连续的线段需要组成一个90度的直角；

       d) 多边形的所有边都要平行于坐标轴；

       e) 多边形不能存在自交；

       f) 多边形的周长要满足最小；

       题解：

       1) 对于输入的点保存两份数组PX、PY，并且记录每个点在原数组的下标index；

       2) 对PX进行X优先排序，对PY进行Y优先排序；

       3) 对PX中序号为奇数的点PX[i]和它的下一个点PX[i+1]进行y值的判断，如果这两个点的y值不相等，那么说明这个点无法加入多边形中（PX[i]无法配对，被孤立了），无解。否则PX[i].index和PX[i+1].index必然有一条边（可以用邻接表来存边关系，因为最后求的是一个多边形，所以每个点有且仅有两条边，其实就是一个哈密尔顿回路）。

          并且加PX[i+1].x - PX[i].index 累加到答案ans中；

       4) 对PY中的点作和3）一样的处理，保存边的关系，但是这里需要判断一种自交的情况，如图1中，3)操作完毕后，产生三条边(1,1) - (2,1)  (1,2) -(3, 2)   (2,3) - (3,3)；那么在进行操作4）的时候(1,1)-(1,2) 和 (3,2) - (3, 3)都是没问题的，唯独 (2,1) - (2,3) 和 先前的边 (1,2) -(3, 2) 会产生自交，违反了e这条规则，所以需要检测这种情况是否存在，如果存在，那么必然无解；具体检测方法很多，不再累述；

图1

       5) 进过3)和4)后，再进行一次连通性判断即可，以防图2的情况。

图2

129 Inheritance

      解析几何 + 凸包 + 线段判交

         题意：给定一个多边形和若干线段，这个多边形内任意两点连线不会和多边形边界相交，分别求这些线段在多边形内部的长度。

         题解：首先，根据“多边形内任意两点连线不会和多边形边界相交”可以肯定这是个凸多边形，于是问题就转化成了求某条线段和凸多边形相交后线段在多边形内部分的长度。

         由于给定的点是乱序的，所以最简单的方法是求这些点集的一个凸包，构造出一个按点排序的多边形，相邻两点连线为原多边形的一条边。

那么枚举每条边和给定线段的相交情况：

         1) 不相交（平行），继续判断下一条边；

         2) 共线，直接跳出枚举，（由于是凸多边形，改线段肯定不可能在多边形内）；

         3) 相交，将这个交点存入集合S；

         将原线段的两个端点存入集合S，对集合S的点进行x坐标递增排序（x相同时y坐标递增排序），然后枚举相邻两个点的中点，判断是否在在原多边形内，如果在，那么将这两个相邻点练成的线段的长度累加到最后的答案中。如图1为两个交点的情况。

图1

      计算几何：射线和球体相交

       题意：给定一条3D射线 和 N个球体，问射线的各种反弹经过的球体编号，如果反射超过10次，只需要输出前十次。

       题解：很明显，首先需要枚举每个球体和当前射线的相交情况，如果和多个球体相交肯定是取距离最近的球体进行相交计算，然后计算出空间反射射线，重复以上操作11次，如果某次的反射射线已经不能和任何球体相交那么直接跳出这个过程。

图1

       如图1，表示射线AB和球O相交于B点，反射后的射线为BC，BD为球心O到交点的延长线，那么必定满足以下几个条件：

       已知A点坐标(x_a, y_a, z_a)，单位向量t_ab

       B点坐标 为 (x_b, y_b, z_b)  =  (x_a, y_a, z_a) + |AB| * t_ab   (1)

         B点在球O上，所以B点坐标满足

       | (x_b, y_b, z_b)  - (x_o, y_o, z_o) | = OB = Ro              (2)

       将(1)代入(2)，可计算出|AB|的长度（由于是射线和球体求交，这两个方程求出来的是直线和球体的交点，所以还需要计算方向判断交点的可行性，如果交点有两个，则取距离小的那个，如果只有一个交点，说明是相切），然后利用(1)式计算出B点坐标。

       2) 射线经过球体的反射射线

       假设C点在A经过B点反射后的反射射线上，并且AB = BC，那么AC必定和OB延长线相交，假设交于D点；

       单位向量cos(ABD) = I_{ba ­­}* I­­_bd；

BD = AB * cos(ABD)；

向量AD = 向量AB + 向量BD；

向量AC = 2 * AD；

点C (x­_c, y_c, z_c) = 向量AC + (x_a, y_a, z_a)；

向量BC求出后返回1) 继续判断和别的球的相交情况；

111 Very simple problem

       二分答案 + 大数模拟

       题意：给定X( X <= 10¹⁰⁰)，求X开方后的下取整。

       题解：数组模拟大数。二分答案A，找满足 A*A <= X 最大的A即为答案。

 
112 a^b-b^a

       二分求幂 + 大数模拟

       题意：求 a^b - b^a ( 0 < a, b < 100)。

       题解：数组模拟大数。二分求 A^B。

       当 B == 0  则 A^B = 1; 否则 A^B = (A²)^(B/2) * ( (B mod 2) ? A : 1 ); 递归求解。

113 Nearly prime numbers

       素数筛选 + 素数判定

       题意：判断一个数是否为两个素数的积。

       题解：利用传统的素数筛选将 1-31623 的素数筛选出来，31623为平方大于等于10⁹的最小整数，因为一个数的开方内找不到一个(非1或它本身)因子的话它本身就是素数，所以素数只需要筛选到 10⁹ 的开方 即可。

       对于每个数，遍历素数数组，如果能被某个素数整除，判断商是不是一个素数，如果商也是素数结果为Yes，否则为No。

114 Telecasting station

      枚举 + 统计

       题意：在X轴上规定一些有权值a­i的点 (x1,a1), (x1,a1), (x2,a2) .. (xn,an)要求在x坐标上找到一个点X使得 M = |X-x1|*a1 + ... |X-xn|*an 的值最小。

       题解：细心观察可以发现，M是关于X的一次函数，所以可以确定X必定为 x1...xn中的某个点。

       由于原式中存在绝对值，为了将绝对值化简，可以将X的区间分段，比如当X 为 xj时可以简化为 M = (X-x1)*a1 + ...(X-xj)*aj + (xj+1-X)*aj+1 + ... + (xn-X)*an

            = (X * presum[j] - preproduct[j]) + (postproduct[j+1] - X * postsum[j+1])

 
图2

      这些辅助数组可以通过四次线性扫描得出，复杂度O(n)。然后，先将xi递增排序，枚举每个xi，计算最小值更新M，就可以在O(n)的时间内求解了。总体算法复杂度为排序复杂度O(n log n)。


115 Calendar

       简单模拟

       题意：给定一个月份M和天数N，求2001的那一天是星期几。

       题解：可以预处理出每个月的天数，如果天数大于那个月对应的天数或者月数大于12肯定是不可行的，否则将给定月数M之前的 1到M-1个月的天数相加再加上N得到Sum，Sum mod 7就可以定位到星期几了。

A . John

PKU 3480 http://poj.org/problem?id=3480

题意：N堆石子，两人轮流从其中一堆中取任意石子，最后一个取完石子的人输。

题解：博弈。

1) 当所有石子的SG值异或和不等于0时：

a) 个数大于1的堆数=0，必定是奇数个1，所以先手必输；

b) 个数大于1的堆数=1，总能想办法将局面变成奇数个1，所以先手必胜；

c) 个数大于1的堆数>1，总能取掉某些石子，使得所有石子的SG值异或和为0，并且个数大于1的堆数至少还剩两堆；

2) 当所有石子的SG值异或和等于0时：

a) 个数大于1的堆数=0，必定是偶数个1，先手必胜；

b) 个数大于1的堆数=1（不存在）；

c) 个数大于1的堆数>1，无论怎么取，SG值异或和都不可能为0。并且无论先手怎么移，后手可以要么进入偶数个1的状态，要么保持SG值和为0并且非全1的状态（该状态先手必输），所以这种情况，先手必败。

由于1) 的c)情况可以到达2的c)情况，所以1的c)情况为先手必胜点。

B . Double Queue

PKU 3481 http://poj.org/problem?id=3481

题意：给定一些数据(K,P)和一些询问，K为数据值，P为优先级，每次询问输出当前优先级最高或者最低的数据的K的值，询问完删除这个数据。

题解：平衡树。

可以用SLT的set(内部也是平衡树的实现)水过去。

C . ‘JBC’

PKU 3482 http://poj.org/problem?id=3482

题意：进制转换，数字位可以是任何的可见ASCII码，求所有可能进制下的串转换成十进制后的和。

题解：模拟进制转换，模拟大数运算。

D . Loan Scheduling

PKU 3483 http://poj.org/problem?id=3483

题意：给定N(N <= 10000)个任务，每个任务是一个二元组(Pi, Di)，表示如果在[0, Di]的某个时刻内完成则可以得到Pi的利润，每个时间点最多只能有L(L <= 100)个任务，求取一个任务子集来完成的的最大利润总和。

题解：贪心。

初始化每个时间点的可用任务数为L，初始化任务利润和S。

将所有任务按Pi从大到小排序，对于每个任务，从Di到0枚举它的完成时间t，如果t这个时间点还有可用任务，累加Pi到S，并且将t这个时间点的可用任务数减1，枚举完所有任务后S即为所求。

E . Showstopper

PKU 3484 http://poj.org/problem?id=3484

题意：给定一些三元组(X, Y, Z)，一个三元组表示满足X + K*Z <= Y (K = 0, 1, 2, 3 ... ) 的所有正整数 X + K*Z出现了一次。对于多个三元组，保证所有数中至多只有一个数出现奇数次，求这个数以及它出现的次数。

题解：二分答案。

对于出现奇数次的那个数T，那么如果小于T的所有数的和必定是偶数，大于等于T的所有数的和必定是奇数，利用这一点可以二分枚举这个T，然后利用所有小于等于T的数的个数的奇偶性进行二分判定。

对于某个三元组(X, Y, Z)，小于等于T的个数分几种情况讨论：

1) 当T >= Y，个数为 (Y-X)/Z + 1;

2) 当T < X，个数为0;

3) 当 X <= T < Y，个数为 (T-X)/Z + 1;

每次枚举T，将所有区间的数相加判断奇偶性即可。

F . Highway

PKU 3485 http://poj.org/problem?id=3485

题意：给定一条高速公路的长度L(范围为0到L)和N个村庄，要求在高速公路上建一些出口，使得每个村庄到高速公路至少有一个出口的距离不大于D，并且出口总数最少。

题解：贪心。

计算出每个村庄到高速公路距离D范围内的左右区间[Li, Ri]，对这些区间进行排序，排序规则为如果左端点一致则按照右端点递增排序，否则按照左端点递增排序。然后按左端点递增枚举每个区间（每个区间对应一个村庄），对于尚未有高速公路可达的村庄，在其右端点建立一个出口（贪心所在，因为是从左往右扫描，所以在右端点建出口肯定比左端点建更优），然后将它之后的左端点坐标小于这个出口的区间全部hash掉（因为那些村庄可以用这个出口，无须建立新的出口），直到所有区间枚举完毕，出口数也就得出了。

G . Computers

PKU 3486 http://poj.org/problem?id=3486

题意：故事背景是每年都要更换电脑或者进行一次维修，如果换电脑需要c的花费，如果不换电脑，那么第y年到第z年( 1 <= y <= z <= n)的总维修费用为m[y][z]，求经过n年的最小花费。

题解：动态规划。

DP[i]表示经过i年的总开销，假设从第j年开始买了一台新的电脑，一直用到了第i年，那么前j年的总开销为DP[j]，从第j+1年到第i年的维修开销加上购买花费c，即DP[j] + m[j+1][i] + c，DP[i]就是这些开销中的最小值，即。

DP[i] = min{ DP[j] + m[j+1][i] + c, 0 <= j < i };

H . The Stable Marriage Problem

PKU 3487 http://poj.org/problem?id=3487

题意：n(n < 27)对男女，每个男人有对所有女人的好感度，每个女人也有对所有男人的好感度，A对B的好感度记为G(A, B), 求找出一种稳定的婚配关系，使得对于任意一对夫妇X(M, W)，不存在 G(XM, YW) > G(XM, XW) 并且 G(XW, ZM) > G(XW, XM)，并且要求男士优先考虑（即男方如果能找到好的一定不会更差的）。通俗的讲，就是XM更加喜欢别人的老婆，Xw更加喜欢别人的老公，这样的婚姻是不稳定的，双方都有可能出现外遇。

题解：稳定婚姻经典算法。

由于是男士最优，所以需要模拟男士求爱的方式。

用L[i][j]表示i号男子喜欢的第j个女子的编号；

用R[i][j]表示i号女子对j号男子的评分（越大评分越高，且对于确定的i肯定互不相同）；

算法如下：

1) 将所有的男子以及他们向多少个女人求过婚的信息入队，每次弹出一个男子M，找到他下一个要求婚的对象（求婚顺序按照对女生的好感度顺序进行）。

a) 如果当前求婚对象W没有配偶，直接配对，记Match[ W ] = M;

b) 如果当前求婚对象有老公，即Match[ W ]，那么检查M 和 Match[ W ]在W的评分，如果M的评分大于W的老公，则迫使其改嫁，前夫入队，Match[ W ] = M；否则，该男子M继续入队；

2) 反复进行1)直到所有人都找到的对象。

I . Arne Saknussemm

PKU 3488 http://poj.org/problem?id=3488

题意：简单字符串模拟。

题解：根据题意做就行了。

A.Nth Largest Value
       PKU 3781 http://poj.org/problem?id=3781

水题，求10个数中第3大的数。

B.Equal Sum Partitions
       PKU 3782 http://poj.org/problem?id=3782

       题意：给定一个M(M <= 10000)个元素的序列，将它切割成K块，每块的和相等，求最大的K。

       题解：枚举。

       首先，切成K块，每块和相等，那么这个和必定是M个元素总和的一个因子，那么可以枚举第一个块的长度（M种），判断当前块的和是否能被所有数的总和整除，如果可以，顺序判断可行性，看似复杂度是O(M^2)，但是能否整除这个剪枝可以筛选掉绝大部分情况。

C.Balls
       PKU 3783 http://poj.org/problem?id=3783

题意：给定B (B <= 50) 个一样的球，从 M (M <= 1000) 层楼上一个一个往下扔，存在某个楼层K，使得低于它的楼层往下扔球，球不会碎，在第K层扔下去会碎。求最坏情况下，需要扔几次才能确定这个K。

题解：动态规划。

令DP[i][j]表示总楼层为i，持有j个球时，最坏情况需要的次数；

那么如果从k ( 1 <= k <= i) 层进行扔球，有两种情况：

1) 如果球不碎，则还需要进行DP[i-k][j]次测试（向更高的楼层进发）；

2) 如果球碎，那么还可以进行的次数为DP[k-1][j-1] （损失了一个球）；

由于要考虑最坏情况，所以每次测试必须取(1) (2)中的大者+1，每次选定一个楼层，使得这个楼层往下扔球的结果的最大值最小，也即状态转移方程为：

DP[i][j] = Min( DP[i][j],  Max(DP[i-k][j], DP[k-1][j-1]) + 1 );

Pku上有道和这题想法类似的题：http://poj.org/problem?id=1243

D.Running Median
       PKU 3784 http://poj.org/problem?id=3784

       题意：一个长度为M(M <= 9999)的序列，每次奇数位的数读入的时候计算前面整个序列的中位数。

       题解：二分 + 树状数组。

       由于数字是int32范围，所以首先需要将所有数离散到下标，枚举每一个数字读入，将对应位的数字下标插入到树状数组中，每当读到奇数个的时候，利用树状数组的成端求和的性质，如果要找第K大的数，那么就二分一个答案，然后查询树状数组，如果求和大于等于K，表示是一个候选解（因为要保证大于等于K的数最小，才是第K大的数），反复二分，直到找到最小的值V满足sum(V) >= K，时间复杂度O(2 *M * log(M) )。

E.The Next Permutation
      PKU 3785 http://poj.org/problem?id=3785

题意：给定一个可重复元素的排列A[i]，求下一个排列。

题解：从后往前扫描，对于第i个元素A[i]，如果能够找到一个j，使得A[j] > A[i]，并且满足A[j]是继第i位之后最小的数，那么将A[i]和A[j]进行交换，然后将A[i+1]到末尾的元素进行一次不降序排序，最后得到的串就是解。

F.Adjacent Bit Counts
      PKU 3786 http://poj.org/problem?id=3786

题意：求长度为n的二进制整数中，相邻两个1的对数有k对（可重复使用）的整数个数。

题解：动态规划。

令长度为n，相邻1的对数为k的数的个数为DP[n][k]，其中以0结尾的为DP[n][k][0]，以1结尾的为DP[n][k][1]，那么 DP[n][k] = DP[n][k][0] + DP[n][k][1]；

并且有如下状态转移方程：

1) 长度为n-1的二进制数在末尾加上一个0，相邻1的对数不变，所以有：

DP[n][k][0] = DP[n-1][k][0] + DP[n-1][k][1];

2) 长度为n-1的二进制数在末尾加上一个1，相邻1的对数取决于，第n-1位是0还是1，当第n-1位是1，相邻1的对数+1；当第n-1位是0，相邻1的对数不变，所以有：

DP[n][k][1] = DP[n-1][k][0] + DP[n-1][k-1][1];

并且初始状态下DP[0][0][0] = 1,  DP[0][0][1] = 0

G.Convex Hull of Lattice Points

PKU 3787 http://poj.org/problem?id=3787
     题意：凸包。

题解：Graham扫描法求解即可。

H.Interior Points of Lattice Polygons

PKU 3788 http://poj.org/problem?id=3788
     题意：给定一个凸多边形，求它内部所有的水平线段。

题解：从多边形第一个点的y坐标开始，递减枚举水平线段的y坐标，分别和多边形的n条边进行求交点；

1) 如果水平线段和多边形某条边共线，说明正好到了多边形的边缘，无须往下枚举，跳出循环。

2) 如果水平线段和多边形小于一个交点，那么当y轴再次减小的时候，必然没有交点，也无须继续枚举。

3) 否则，将左端点坐标取上整x1，右端点取下整x2，如果x1 <= x2 将它插入到解集中。

       题意：给定一个一维的棋盘，范围为[0, W] (W <= 1000,000,000)，某两个点之间有梯子或虫洞，梯子的下端点到上端点以及虫洞的上端点到下端点花费的步数为0，其它任意点之间的距离通过跳跃来计算，最多每次跳跃不超过S格（S<= 6），跳跃的过程中如果跳到梯子的下端点或者虫洞的上端点就会被直接传送到另一端，并且每次跳跃只能从小的点跳到大的点（虫洞是个例外），求从0到W的最短距离。

图A-1

       题解：

              离散化 + SPFA。

       将所有梯子和虫洞的两端点、0和W以及他们往前往后S步以内的数全部记录下来，梯子和虫洞有P（P <= 40）个，加上起点终点，总共82个点，算上前后各六步，总共82 * 13 = 1066个点，然后将这些点排序后离散化，最后就是要构建一个网络图，通过网络求0到W的最短路，最短路可以用SPFA求解。

       谈谈建图的过程，对于任意两个点，他们之间必定可以连一条边，然后有一个步数表示边的权值（这里的步数也可能是正无穷，也即永远都无法到达）。

       对于任意两个点(u, v)，他们的步数w(u, v)（边权）我们做如下讨论（这里的u、v是离散化后的点）：

       1）如果u是梯子的下端点，v是梯子的上端点 或者 u是虫洞的上端点，v是虫洞的下端点，那么w(u, v) = 0，否则进入2)的判断;

2）如果u的编号大于v，w(u, v) = inf，表示永远不可达，因为某次跳跃只能从小的点跳到大的点，否则进入3）的判断;

3）如果u的实际位置和v的实际位置差值小于等于S，则w(u, v) = 1；

4）检查u和v之间是否有虫洞的上端点或者梯子的下端点，之后将这两种点称为X点

a）如果有，判断他们是否连续，

i) 如果不连续w(u, v) = inf（这一步这么做是为了简单化，试想一下，如果X点不是全部连续，说明u可以先跳到他们中间的某个非X的点，然后再跳到v点，这一步是通过SPFA来实现迭代的，建边的时候可以不考虑）。

ii）如果连续，判断他们连续的格子的数目，如果大于等于S说明这个连续的块必定跳不过去，所以w(u, v) = inf，否则可以先跳到最先的一个X点的前面一个点，然后经过一步S跳跃将这个连续块跳过去，再跳到v。

              b）如果没有X点，那么直接从u点跳到v点。

       这里我们需要计算从a点跳到b点不考虑虫洞和梯子的最短距离，可以贪心的跳，每次往大的跳，直到剩余格子不足S格，即(b-a + S-1) / S （b-a对S求商的上整）。

       边建立完成就可以利用广搜求解0-W的最短路了。

B. Gnome Sequencing
       PKU 3913 http://poj.org/problem?id=3913

       水题，判断三个数是全递增还是全递减还是无序。

C. DuLL
       PKU 3914 http://poj.org/problem?id=3914

       题意：给定一些dll文件和它占用的内存空间，以及一些可执行程序占用的内存空间和它依赖的dll文件，程序以进程为单位，两个相同的程序可能有不同的进程，进行一些下列的操作：

       1）某个程序运行的时候需要它依赖的dll文件也加载到内存中，多个程序可以共用一个dll文件；

       2）某个程序退出的时候，如果它所依赖的dll文件没有其它程序使用，需要释放这段内存空间；

       给定一系列的运行进程，求某个时刻的最大内存占用。

       题解：HASH的简单应用。

       初始化内存占用V = 0，

       对于给定的输入进程：

       1）如果是新运行的进程，将V加上这个进程的内存占用，并将它所有依赖的dll文件检查一遍，如果引用计数为0，则将对应dll文件的内存累加到V上，引用计数+1；

       2）如果是退出进程，将V减去这个进程的内存占用，并将它所有依赖的dll文件检查一遍，如果引用计数为1，则用V减去对应dll文件的占用量，引用计数-1；

       每次操作记录最大的V就是最后的答案。

D. Black Vienna
       PKU 3915 http://poj.org/problem?id=3915

       题意：三个人，每个人五张牌，互相不知道对方的牌，还有额外的三张牌放在一边（所有牌编号为A - R）。每一轮，由 (i-1)%3+1 (1 <= i <= 15) 号玩家进行发问，问Ai  (1 <= Ai <= 3) 号玩家XYZ（代表任意三个牌号）三张牌中有多少张在他手上，然后他回答Bi (0 <= Bi <= 3)，问经过多少轮之后有某位玩家知道 额外 的那三张牌是什么。

      题解：dfs枚举 + 剪枝。

       首先枚举到某个询问i的时候玩家j能够猜出的那三张牌的情况，如果枚举完所有情况最后确定只有一个解满足条件的时候，那个询问的编号i就是答案了。

       类似IDA*的思路，先枚举询问最大深度，如果到达那个询问不能确定额外的那三张牌或者有很多种情况，那么说明还需要更多的询问，迭代深度继续枚举。

       对于某个询问i，找到询问的那三张牌中已经是Ai号选手的数量ansCnt，以及尚未确定牌的归属的牌的数量xCnt，如果已经确定位置的牌数量 大于 实际他回答的数量（ansCnt  >  Bi）或者 尚未确定位置的牌数量 + 已经确定为他的牌数量 小于 实际他回答的数量（ansCnt + xCnt < Bi）都是不合理的情况，剪枝，不用继续往下搜索；

       否则，将(Bi - ansCnt)张牌分配给Ai，(xCnt - (Bi - ansCnt))张牌分配给其它两位玩家以及额外的那一堆，这里需要用到嵌套dfs枚举，枚举完后进入下一个询问的枚举，每次询问的时候可以有几个剪枝：

       1）如果某个阶段某个人的牌数超过5张；

       2）枚举的解的数量超过2个；

       3) 对于一次完全枚举，枚举完所有询问后还是有无法确定三张额外的牌的情况；

E. Duplicate Removal
       PKU 3916 http://poj.org/problem?id=3916

       水题，对输入的元素进行连续判重输出。

F. Rock, Paper, Scissors
       PKU 3917 http://poj.org/problem?id=3917

       水题，剪刀石头布！O_o

G. A to Z Numerals
       PKU 3918 http://poj.org/problem?id=3918

       题意：复杂模拟。（没做出来，#-_-# 样例的98是怎么出来的呀！！！）

H. Cell Towers 
       PKU 3919 http://poj.org/problem?id=3919

       题意：给出一条曲折的连续线段，曲线从起点开始每经过一个长度为1的单位会放置一个守卫K，在曲线以外的某些地方会有T(T <= 10)个信号发射器，用A、B、C...来表示，每个信号发射器有它的信号强度Pi，每个信号发射器到守卫K的距离如果是D，那么它能接收到的信号值为Pi / D²的最近整数，并且对于守卫K，它只会接收最大的信号值，如果有多个发射器对于K的信号值相同，那么选择字典序最小的发射器。需要求是一些守卫集合，这些守卫分别和它的前一个守卫所接收的信号发射器不一样。

       题解：计算几何、向量的简单应用。

       对于每条射线，终点减去起点，再单位化后就可以得到这条射线的单位向量，利用这一点可以很简单的将所有守卫的坐标求出来，然后对于每个守卫判断接收的是哪个发射器，判断和之前那个守卫是否相同即可。

       需要注意的是最后一个守卫，当和上一个守卫距离小于0.5的时候不会建立新的守卫。

I. RIPOFF
       PKU 3920 http://poj.org/problem?id=3920

       题意：给定N(N <= 200)个数的一维数组A，取不大于T+2个数，每相邻两个数之间的下标不大于S，问最大的取值总和(第0个和第N+1个数必取，且权值为0)。

       题解：动态规划。

       DP[i][j] 表示第j个数取 A[i]的最大值，那么状态转移方程可以表示为：

       DP[i][j] = max{ DP[k][j-1] + A[i],  i > k > i-1-S && k >= 0};

       特殊的，DP[0][0] = 0，其他的DP[i][j] 都初始化为INF;

       最后计算出的DP[N+1][i]中的最大值就是答案了。

       题意：给定一个3X3的六面魔方（每个面有3X3个块），求经过某些旋转之后能否使得所有面的颜色都相同，旋转包括对某个面进行顺时针和逆时针旋转（共12种情况）。

图A-1

       如图1，输入数据为左图的形式，右图给对应的面编号，箭头方向为顺时针旋转方向。

+A表示对A这个面进行一次顺时针旋转，-B表示对B这个面进行一次逆时针旋转。问经过一定的+A/-B操作之后能否使得所有面的3X3个字母都相同。

       题解：模拟题

       做法很多，这里介绍一种比较容易理解的状态记录方式，考虑某次旋转，一定是旋转某个面，然后对邻接的四个面的某条边进行顺次平移。如图A-2, 2号面的旋转带动的是1、5、3、6四个面。

图A-2

       我用一个数组rotate_n来记录某个面旋转的时候带动的面的编号集合（编号为0的数据为占位符），那么有：

int rotate_n [7][4] = {

    {0, 0, 0, 0}, {4, 5, 2, 6}, {1, 5, 3, 6}, {2, 5, 4, 6}, {3, 5, 1, 6}, {1, 4, 3, 2}, {1, 2, 3, 4}

};

       光记录带动的面是哪些还不够，还需要知道带动面的对应边，对于一个魔方的一个面，我们编号如下：

（0,0）（0,1）（0,2）

（1,0）（1,1）（1,2）

（2,0）（2,1）（2,2）

       分别用1到4来代表一个面的四条边（注意，有方向）：

1 (0,2) - (0,0)

2 (2,2) - (0,2)

3 (2,0) - (2,2)

4 (0,0) - (2,0)

       那么同样用rotate_p来记录某个面旋转的时候带动的面对应的边，则有：

int rotate_p[7][4] = {

       {0, 0, 0, 0}, {2, 4, 4, 4}, {2, 3, 4, 1}, {2, 2, 4, 2}, {2, 1, 4, 3}, {1, 1, 1, 1}, {3, 3, 3, 3},

};

       这样一来，我们只需要考虑一个面的旋转，然后套用对应的数据即可，还有一个比较巧妙的是，逆时针旋转不需要特殊处理，直接将顺时针旋转执行三次即可。

B．This Sentence is False
       PKU 1291 http://poj.org/problem?id=1291

       题意：给定一些句子形如“Sentence X is true/false”的句子，X表示第几个句子，问所有的情况是否合法，如果合法，输出最大的可能为真的句子。

       题解：2-sat。

       每个句子抽象成两个结点，为真的时候为X，为假的时候为X '。

       a) 对于第X个句子，如果是 Sentence Y is true；

              则这个句子为真的时候， X ->Y连边；

              当这个句子为假的时候，X ' -> Y '连边；

       b) 对于第X个句子，如果是 Sentence Y is false；

              则这个句子为真的时候， X ->Y '连边；

              当这个句子为假的时候，X ' -> Y连边；

       然后求一次强连通，如果最后有某个点X和X ' 在同一个连通图中，说明逻辑错误，说明必然存在不合法的情况，否则对于每个连通分量，求出为真的点的个数和为假的点的个数，然后将他们之中的大者累加，最后答案除2就是最大的可能为真的句子（除2的原因是因为真假是对称的）。

C．Will Indiana Jones Get There?
       PKU 1292 http://poj.org/problem?id=1292

       题意：营救公主，营救路线要么绕着墙走，要么走两面墙的最短距离（这种情况下需要在两面墙之间搭一块木板，并且可以反复使用）。问营救过程中木板的最短长度。

图C-1

       题解：线段距离 + 二分答案

       因为木板可以反复使用，所以我们可以假设如果木板越长，能够营救公主的概率就越大，反之则越小，所以问题就是求满足两点可达的最小木板长度，可以二分枚举这个长度T，如果两面墙的最短距离大于这个T，表明两面墙不可达，将墙抽象成点，两面墙之间的最短距离可以通过线段和线段的最短距离预处理出来，然后每次二分答案后通过一次搜索就可以找出起点和终点是否可达，复杂度为O（n^2）即计算两线段距离时候的复杂度。

D. Duty Free Shop
       PKU 1293 http://poj.org/problem?id=1293

       题意：给定M(M <= 1000)个白巧克力和L(L<= 1000)个黑巧克力，然后给定N(N <= M + L)个容量为Ci的盒子，问能否找到一种方案，使得某些盒子放满白巧克力，剩下的盒子放满黑巧克力。

       题解：背包问题。

       由于需要将每个盒子都放满，于是可以利用一维背包的求法将Ci的所有小于等于M的可行组合求出来，找到最大的M ' <= M，并且M ' 能够通过某种方式被组合出来，那么所有盒子的容量Sum 减去 M ' 的差小于等于L的话，必定能将剩下的盒子填满黑巧克力，否则无解。

       这题需要记录前驱，并且注意M = 0 以及 L = 0 的情况（主要是在输入的时候判断退出条件，M+L==0退出而并非 (M&&L) == 0）。

E．Not Too Convex Hull
       PKU 1294 http://poj.org/problem?id=1294

       题意：给定N(N<=101)个点（没有三点共线的情况），要求用B(B<=50)根皮条将这N个点圈成B个部分，每个部分为一个凸多边形，并且所有凸多边形公用一个点（这个点会给出），求众多方案中满足所有多边形面积和最小的方案。图E-1表示用两根皮条圈住19个点的情况（原点共用了两次）。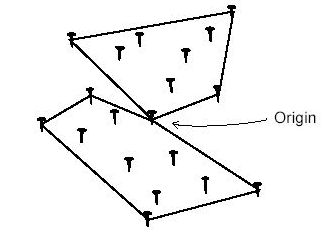

图E-1

       题解：环形动态规划。

       首先将所有点按照给定的原点进行极坐标排序，那么第1个点到第N个点必定是按照极坐标严格逆时针排布的（因为没有三点共线），用DP[i][b]表示第i个点到第N个点经过b次分割后分割完的凸多边形的面积总和最小值，那么：

DP[i][b] =min{ area[i][k] +DP[k+1][b-1]   (i < k < N) }; 特殊的，DP[0][0] = 0;

     area[i][j] 表示极坐标在第i个点和第j个点之间的所有点(包含这两个点)加上原点组成的凸包的面积，可以通过初始化预处理出来；

     由于点是极坐标排列的，也就是第一个点不一定是凸包边上的点（有可能是第N-1个点到第2个点组成的凸包达到整体最优），所以需要做N次DP，可以将所有点复制一份，枚举起点i ( 1 <= i <= N)，终点即i+N, 然后分别做一次DP取最小值。

     时间复杂度O(N^2 * B)。

F．I hate SPAM, but some people love it
       PKU 1295 http://poj.org/problem?id=1295

       题意：N(N<=20)个人互发邮件，某个人收到邮件后一定会回复给他所有的好友，回复的数量决定他的称号，按顺序给定首先发起邮件的人，要求按顺序输出所有人得到的称号。

       题解：深搜枚举。

       数据量很小，对于给定的初始者作为起点进行遍历，每个人只访问一次，访问到的时候根据他的朋友数量计算他的称号即可。

G．Noise Effect
       PKU 1296 http://poj.org/problem?id=1296

       题意：给定两个正方形矩阵，求他们的最大相似度，相似度的定义为矩阵元素对应位差值小于等于100的个数占所有矩阵元素的百分比（可以进行旋转和翻转）。

       题解：模拟题。

       每个矩阵可以进行四次旋转，每次旋转可以有水平翻转、竖直翻转、水平竖直翻转、保持原样四种状态，一共十六种情况（实际小于16种，因为有些状态经过翻转和旋转之后是一样的），对每种情况模拟计算相似度取最大值即可。

H．Supermarket
       PKU 1297 http://poj.org/problem?id=1297

       题意：约翰需要买M(M<=100)件物品，超级市场上的物品都排成一排，一共N(N<=100000)件物品，他从左向右开始选物品，但是为了不麻烦，不想走回头路，而且第i个物品买的条件是，前i－1个物品必须已经买了，但是每个物品在超级市场中的价格不一样，即使同一个物品也有不同的价格，为了花费最少，他想要一个方案使得：

       1) 按顺序购买M个物品；

       2) 总价值最少，并输出这个最小值，如果方案不存在，输出Impossible。

       题解：动态规划。

       DP[i][j]表示第i个购买列表中的物品和第j个市场中的物品匹配时的最小消费（1<=i<=M,1<=j<=N）;

       Min[i][j]表示min{ DP [i][x]  x<=j };

    a)当第i个物品和第j个市场物品编号相同时，DP[i][j] = Min[i-1][j-1] +cost[j];

       b)否则DP[i][j] = inf; 计算DP数组同时更新Min数组，由于每次的状态最多和上一行有关，所以在进行状态转移的时候可以采用滚动数组。时间复杂度O(NM)。

【开发信息】
      本游戏是采用Python的Pygame包开发而成，游戏的模式是射击类型，同时添加了RPG游戏特有的情节模式。

【版本信息】
      v1.00

【游戏简介】

    游戏的主要操作是键盘，但是在确认的时候也可以采用鼠标，鼠标还可以进行人物菜单栏
的Tip的查看，主角主要有生命、魔法、灵魂、攻击力、防御力、速度等几项属性。
    生命值    传说中的血，中国古代角色扮演游戏里大多将它称为“精”。
    查克拉    中国古代游戏中所谓的内力，小时候智力卡游戏中的MP，决定你进行攻击时候同时释放的武器数目。
    灵魂      每次生命值达到负值的时候可以通过释放一个灵魂来将血补满。   
    攻击力    主角自身攻击力和当前武器攻击力的总和，影响对敌人的伤害值。
    防御力    主角的自身防御，影响主角受到攻击时的伤害值。
    速度      决定主角的移动速度和闪避率。
    必杀技    可以作用于整个游戏世界的无敌必杀技，可以理解为“大招”。
    得分      每打到敌人一次可记一分，打死敌人记三分。当得分积满2000的时候可以换赎一个灵魂。

【游戏操作】
      方向键        控制人物行走
      左Ctrl键      发射子弹 + 确认操作
      空格键        释放大招（必杀技）

【几点说明】
      本游戏部分资源取自网络，部分由作者原创，所以请勿将其用于商业用途，否则后果自负。

【试玩链接】
http://code.google.com/p/sguzty/downloads/list

【联系作者】

博客:www.cppblog.com/menjitianya

 邮箱:menjitianya2007@163.com

 QQ:277055227  周天涯 （英雄哪里出来）

【部分截图】

Tetrix v1.01 版本下载地址：
http://code.google.com/p/sguzty/downloads/detail?name=Tetrix%20v1.01%20Release.rar&can=2&q=

Bug 修正
1.最大的bug是方块掉落的时候会将镂空的格子填满，修改之。
2."方块"旋转的时候不应该有任何效果，先前的版本会改变位置。
3.先前版本长条的旋转比较难看，这次略微好看一点。
4.修改了之前Life和Speed的显示问题。

功能 新增
1.添加了背景音乐和音效。
2.征询网友意见添加了随机种子，每次打开后都会有不同的开局。

背景音乐是 智冠电子 的 单机游戏 <天龙八部> 中 某个场景的背景音乐。
以此怀念我们儿时的单机游戏时代。

并且多谢众多网友们提的意见,你们的支持是我们最大的动力。

以下是其中一种在游戏中添加背景音乐的方法，拿出来分享以下，如果直接采用sndPlaySound是不能达到混音效果的，采用以下方法可以播放背景音乐，然后用sndPlaySound在播放音效，就可以达到混音效果。

void BeginMusic() {
    CoInitialize( NULL );
}

class mp3Player {

    IGraphBuilder* pGBuilder;
    IMediaControl* pMControl;
    IMediaPosition* pMPos;

public:
    void load(char *filename);
    void play();

};

void mp3Player::load(char *filename) {
    CoCreateInstance(CLSID_FilterGraph, NULL,CLSCTX_INPROC, IID_IGraphBuilder, (void**)&pGBuilder);
    pGBuilder->QueryInterface(IID_IMediaControl, (void**)&pMControl);
    pGBuilder->QueryInterface(IID_IMediaPosition, (void**)&pMPos);
    
    char strSoundPath[ MAX_PATH ];
    WCHAR wstrSoundPath[ MAX_PATH ];
    
    GetCurrentDirectory(MAX_PATH, strSoundPath);
    strcat( strSoundPath, "\\" );
    strcat( strSoundPath, filename );
    MultiByteToWideChar(CP_ACP, 0, strSoundPath, -1, wstrSoundPath, MAX_PATH );
    
    pGBuilder->RenderFile(wstrSoundPath, NULL);
}

Pygame游戏开发之四

初学乍练

Pygame中除了Group这个Sprite的容器类，还有一些继承自Group的容器类，它们分别是RenderUpdates、OrderedUpdates、LayeredUpdates、LayeredDirty。

pygame.sprite.RenderUpdates继承自pygame.sprite.Group，它相对于Group的不同点就是重写了Group的draw函数，原型是：RenderUpdates.draw(surface) : return Rect_list它将所有它包含的Sprites绘制到surface上，和Group.draw一样。但是这个函数返回了一系列的屏幕上发生改变的矩形列表，这个矩形列表应该被传递到pygame.display.update中去。

pygame.sprite.OrderedUpdates继承自pygame.sprite.RenderUpdates，它绘制Sprite的时候是以Sprite被添加时的顺序来绘制的。

pygame.sprite. LayeredUpdates绘制的方式和pygame.sprite.OrderedUpdates类似，只是它引入了图层的概念。你可以通过'default_layer'设置默认图层，或者一个整数来表示图层。如果添加的Sprite自己有一个layer的图层属性那么就是用这个，否则在添加Sprite的时候，在pygame.sprite. LayeredUpdates(*sprites, **kwarges)中的**kwarges参数中对layer属性进行设置，如果两者都没有设置，那么系统将采用默认图层。

pygame.sprite. LayeredDirty继承自pygame.sprite.LayeredUpdates，它是DirtySprites的专用容器类，继承了Group的所有操作。

因为我们需要用到DirtySprite，所以之前我们用到的所有Group类都替换成LayeredDirty，而且为了便于扩展，我们将LayeredDirty再封装一层，以便添加新的成员函数。

class gameManager(pygame.sprite.LayeredDirty) :

    def __init__(self, selfdata) :

        pygame.sprite.LayeredDirty.__init__(self)

    def keyevent(self, keypressed) :

        for son in self.sprites() :

            son.keyevent(keypressed)

       定义一个gameManager类，它继承了pygame.sprite.LayeredDirty，并且添加一个keyevent的成员函数，用于对键盘事件进行处理，它的操作很简单，调用它容器里的元素的keyevent函数，它容器里的元素有可能是另一个gameManager、或者是一个单纯的RenderObject。如果是gameManager的话就会进行递归调用，直到是RenderObject，所以我们还要给RenderObject定义一个keyevent函数，像这样：

class RenderObject(pygame.sprite.DirtySprite) :

       … …

    def keyevent(self, keypressed) :

        pass

我们把keyevent定义在基类RenderObject中，并且用pass表示它什么都不做，然后等着子类去实现它。

class Player(RenderObject) :

       … …

    def keyevent(self, keypressed) :

        left_or_right = keypressed[K_RIGHT] - keypressed[K_LEFT]

        up_or_down    = keypressed[K_DOWN] - keypressed[K_UP]

        self.move(left_or_right, up_or_down)

Player是RenderObject的一个子类，我们可以用以上的语句实现Player的行走，keypressed其实是pygame.key.get_pressed()，用于获取当前键盘的某个键是否按下的映射表。

       接下来我们用之前的模块来写一个游戏的背景，利用图4-1的资源拼接出图4-2的图像，并且让它在屏幕Y轴方向进行滚屏操作。

图 4-1

图 4-2

       首先要明确的一点就是图片的四个方向必须是可拼接的，也就是说用9张相同的图片拼成一个九宫格，用肉眼是分辨不出它们是九张图片的，看到的是一个完整的图像。

       我们定义一个RenderBack类：

class RenderBack(RenderObject) :

    def __init__(self, selfdata) :

        RenderObject.__init__(self, selfdata)

              do_init()

def update(self) :

       RenderObject.update(self)

              do_update()

首先确定做这么一个背景需要用到的数据，背景的宽高是肯定要的，而且要求它在Y方向做滚屏操作，所以这个背景的实际的高肯定要比屏幕上显示高还要长（我们假设他是图4-1图片高的整数倍），那么我们用一个四元组(x, y, z, w)来表示需要知道的数据：

x : 背景图资源在images[]的索引号

y : 生成图的宽

z : 生成图的高

w: 生成图在竖直方向的原图图块的数量

这个四元组是作为selfdata被传到__init__函数中进行初始化的，并且可以在配置文件中修改它的值。

       因为最后的图像要进行Y方向的滚屏操作，所以我们还需要定义一个Y方向的偏移量，以便每次绘制的时候进行偏移操作。这样初始化就可以这么写：

self.image       = pygame.Surface( (int(selfdata[1]), int(selfdata[2])) )

self.rect         = self.image.get_rect()

self.source_rect   = self.image.get_rect()

self.backlen      = int(selfdata[3])

self.backimage    = RenderObject( [ selfdata[0] ] )

self.top_offset    = self.backimage.image.get_height() * self.backlen - self.rect.height

这里需要注意的是，LayeredDirty在对DirtySprite进行绘制的时候总是对sprite.image的内容进行绘制的，所以在RenderBack里我们需要额外定义一个backimage来对原图进行缓存，然后通过循环将它blit到image上。这样RenderBack的拥有者才能找到image将它绘制出来。

       对于update函数，每一帧我们需要更新self.top_offset这个Y方向的偏移量，并且根据它更新image图像。具体实现如下：

def update(self) :

RenderObject.update(self)

xstep = self.backimage.image.get_width()

ystep = self.backimage.image.get_height()

self.top_offset -= 3

y_offset = self.top_offset % ystep

for x in range(0, self.rect.width + xstep, xstep) :

self.image.blit( self.backimage.image, (x, 0), ((0, y_offset), (xstep, ystep - y_offset) ) )

for y in range(ystep - y_offset, self.rect.height + ystep, ystep) :

for x in range(0, self.rect.width + xstep, xstep) :

self.image.blit( self.backimage.image, (x, y), ((0,0), (xstep, ystep) ) )

(xstep, ystep)是原图的尺寸，每一帧我们对self.top_offset进行自减操作（效果就是让最后的图像有一种向上延伸的感觉，也就是滚屏的效果）。

然后我们分x方向和y方向进行讨论，因为x方向没有滚屏操作，所以只要用现有的图片填充整个宽度即可，比如原图是W=100个像素，需要填充的背景是D=250个像素，那么水平方向至少需要用到[ (D + W – 1) / W ] = 3张原图（[x]表示比x小的最大整数，即取下整）。对于竖直方向，因为有滚屏操作，所以有两部分组成：第一排（从原图的y方向某个位置粘贴过来的）以及非第一排（总是粘贴原图）。将self.top_offset 对 ystep 取模，得到的是需要绘制图像的最上方在原图的偏移量，通过它可以绘制第一排，然后再调用两层for循环绘制后面几排。这样随着时间的推移，一个Y方向的滚屏效果就出来了。（未完待续）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3756

/**//*
题意：
    在一个三维空间中，给定一些点，这些点的z坐标都是大于0的。要求求
出一个圆锥（底面是圆形），使得这个圆锥的底面在z = 0的平面上，它能够
包含所有给定的点并且圆锥的体积要求最小。

题解：
    数学推导 + 三分

思路：
    这是一个很有意思的题，虽然是三维的，但是可以很容易的转化到二维去
。来看X-Z这个平面，我们将所有的点进行圆周映射，然后将所有的点都投影到
X-Z平面的的第一象限去，然后问题就转化成了在X-Z平面上找到一条斜率为负
的直线L，L和X正方向、Z正方向围成的三角形包含所有点，如果假设L和X轴的
交点为R，和Z轴焦点为H，要求pi*H*R^2的值最小。
    然后我们来看看H和R之间有什么千丝万缕的关系。首先L这条线必定和某一
个给定的点擦边，也就是经过那个点，我们假设它经过P(a, b)， 并且L的斜率
为K(K < 0)，那么L的方程就可以表示为 L:  y = K * (x - a) + b，则H和R就
可以利用这个方程表示出来：
H = -a * K + b;
R = -b / K + a;
那么所求的圆锥的体积就是：
V = pi*H*R^2 = pi * (-a * K + b) * (-b / K + a) ^ 2
容易得到V(K)这个函数的导数：
V'(K) = - pi * (aK^2 + 2bK) * (aK - b)^2 / K^2
影响这个导数的正负性的唯一条件是 -(aK^2 + 2bK)
当-2b/a < K < 0时V'(K)大于零，也就是V的值是随着K递增的。
当K < -2b/a时V'(K)小于零，也就是V的值是随着K递减的。
于是可以得出一个结论，当K = -2b/a 时V取得最小值。
于是我们知道了V的单峰性，然后就可以通过枚举半径R，因为R对于V具有单谷
性，所以枚举R的时候可以采用三分。每次通过三分R找到最小的H，这个过程可
以通过枚举每个点，找到最大的极角alpha，R*tan(alpha)就是H了。
    这里需要注意的就是精度问题了。
*/

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;

#define eps 1e-6
const double pi = acos(-1.0);

struct Point {
    double x, y, z;
    double v, h;

    void SCANF() {
        scanf("%lf %lf %lf", &x, &y, &z);
        v = z;
        h = sqrt(x*x + y*y);
    }
}pt[ 10001 ];

int n;
double MaxH, MaxV;

double Calc(double R) {
    int i;
    double Max = 0;
    int idx = 0;
    for(i = 0; i < n; i++) {
        double nv = pt[i].v / (R - pt[i].h);
        if(nv > Max) {
            Max = nv;
            idx = i;
        }
    }
    return Max * R;
}

int main() {
    int t;
    int i;

    scanf("%d", &t);
    while(t--) {
        scanf("%d", &n);
        MaxH = MaxV = 0;
        for(i = 0; i < n; i++) {
            pt[i].SCANF();
            if(pt[i].h > MaxH)
                MaxH = pt[i].h;
            if(pt[i].v > MaxV)
                MaxV = pt[i].v;
        }

        double l = MaxH + eps, r = 1e6;
        double ml, mr;

        while(l + 1e-6 < r) {
            ml = (2 * l + r) / 3;
            mr = (l + 2 * r) / 3;

            double lans = Calc(ml) * ml * ml;
            double rans = Calc(mr) * mr * mr;

            if( lans > rans ) {
                l = ml + 1e-5;
            }else
                r = mr - 1e-5;
        }
        double ans = (l + r) / 2;
        printf("%.3lf %.3lf\n", Calc(ans), ans);
    }
    return 0;
}