|
|
摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1066
/**//*题意: 给定一个数N(N <= 10^200),求出N的阶乘的最后一位非零数字。题解: 找规律 + 大数模拟思路: &nb... 阅读全文
摘要: 题目链接:http://poj.org/problem?id=3145
/**//*题意: 对于一个集合S,一共两种操作:1. B X: 添加一个数X到S. 第K个B操作发生在第K个时间点,并且每个之前S集合中没有X。2. A Y: 在S集合中所有数中, 被Y除后余数最小... 阅读全文
摘要: 题目链接:http://poj.org/problem?id=1186
/**//*题意: 已知一个n元高次方程: 其中:x1, x2,,xn是未知数,k1,k2,,kn是系数,p1,p2,pn是指数。且方程中的所有数均为整数。 假设未知数1 <= xi <= M,&n... 阅读全文
题目链接:http://poj.org/problem?id=1990
  /**//* /**//*
 题意: 题意:
 约翰农夫有N(N <= 20000)头牛,每头牛有一个权值Vi,他将它们排成一排, 约翰农夫有N(N <= 20000)头牛,每头牛有一个权值Vi,他将它们排成一排,
 牛i和牛j的阈值是 两者的距离差*max(Vi, Vj),现在给出每头牛的权值和它的 牛i和牛j的阈值是 两者的距离差*max(Vi, Vj),现在给出每头牛的权值和它的
 位置,求所有两头牛之间的阈值之和。 位置,求所有两头牛之间的阈值之和。

 题解: 题解:
 树状数组 树状数组

 思路: 思路:
 我们准备两个树状数组,以每头牛的位置作为树状数组的下标,其中一个用 我们准备两个树状数组,以每头牛的位置作为树状数组的下标,其中一个用
 来表示当前位置的牛的位置的值,另一个则记录当前位置牛的个数,然后对所有 来表示当前位置的牛的位置的值,另一个则记录当前位置牛的个数,然后对所有
 牛以Vi为关键字进行递增排序。 牛以Vi为关键字进行递增排序。
 接下来对每头牛进行一次线扫,首先统计比当前这头牛的位置小的和大的牛 接下来对每头牛进行一次线扫,首先统计比当前这头牛的位置小的和大的牛
 的数目和位置和,然后做差求出以当前牛的权值为最大值的阈值总和。之后将这 的数目和位置和,然后做差求出以当前牛的权值为最大值的阈值总和。之后将这
 头牛的数量和位置插入到树状数组中进行更新。 头牛的数量和位置插入到树状数组中进行更新。
 */ */

 #include <iostream> #include <iostream>
 #include <algorithm> #include <algorithm>

 using namespace std; using namespace std;

 #define maxn 20010 #define maxn 20010
 #define ll __int64 #define ll __int64

  struct point struct point  { {
 int V; int V;
 int pos; int pos;
 }pt[maxn]; }pt[maxn];

 ll c[2][maxn]; ll c[2][maxn];
 int n, Max; int n, Max;

  ll ABS(ll v) ll ABS(ll v)  { {
 return v < 0 ? -v : v; return v < 0 ? -v : v;
 } }

  int cmp(point a, point b) int cmp(point a, point b)  { {
 return a.V < b.V; return a.V < b.V;
 } }

  int lowbit(int x) int lowbit(int x)  { {
 return x & (-x); return x & (-x);
 } }

  void add(int idx, int pos, int v) void add(int idx, int pos, int v)  { {
  while(pos <= Max) while(pos <= Max)  { {
 c[idx][pos] += v; c[idx][pos] += v;
 pos += lowbit(pos); pos += lowbit(pos);
 } }
 } }

  ll sum(int idx, int pos) ll sum(int idx, int pos)  { {
 ll s = 0; ll s = 0;
  while(pos > 0) while(pos > 0)  { {
 s += c[idx][pos]; s += c[idx][pos];
 pos -= lowbit(pos); pos -= lowbit(pos);
 } }
 return s; return s;
 } }


  int main() int main()  { {
 int i; int i;
  while(scanf("%d", &n) != EOF) while(scanf("%d", &n) != EOF)  { {
 Max = 0; Max = 0;
  for(i = 0; i < n; i++) for(i = 0; i < n; i++)  { {
 scanf("%d %d", &pt[i].V, &pt[i].pos); scanf("%d %d", &pt[i].V, &pt[i].pos);
 if(pt[i].pos > Max) if(pt[i].pos > Max)
 Max = pt[i].pos; Max = pt[i].pos;
 } }

 for(i = 1; i <= Max; i++) for(i = 1; i <= Max; i++)
 c[0][i] = c[1][i] = 0; c[0][i] = c[1][i] = 0;
 sort(pt, pt + n, cmp); sort(pt, pt + n, cmp);

 ll ans = 0; ll ans = 0;
  for(i = 0; i < n; i++) for(i = 0; i < n; i++)  { {
 ans += ABS((sum(0, Max) - sum(0, pt[i].pos) ans += ABS((sum(0, Max) - sum(0, pt[i].pos)
 - (sum(1, Max) - sum(1, pt[i].pos)) * pt[i].pos)) * pt[i].V; - (sum(1, Max) - sum(1, pt[i].pos)) * pt[i].pos)) * pt[i].V;

 ans += ABS((sum(0, pt[i].pos) ans += ABS((sum(0, pt[i].pos)
 - sum(1, pt[i].pos) * pt[i].pos)) * pt[i].V; - sum(1, pt[i].pos) * pt[i].pos)) * pt[i].V;

 add(0, pt[i].pos, pt[i].pos); add(0, pt[i].pos, pt[i].pos);
 add(1, pt[i].pos, 1); add(1, pt[i].pos, 1);
 } }
 printf("%I64d\n", ans); printf("%I64d\n", ans);
 } }
 return 0; return 0;
 } }
题目链接:http://poj.org/problem?id=2828
  /**//* /**//*
 题意: 题意:
 给定N(1 <= N <= 200000)个整数对(A,B),表示在A右边的位置插入一个B, 给定N(1 <= N <= 200000)个整数对(A,B),表示在A右边的位置插入一个B,
 经过N次操作后问最后的B序列的排列情况。 经过N次操作后问最后的B序列的排列情况。
 题解: 题解:
 树状数组 或者 线段树 树状数组 或者 线段树

 思路: 思路:
 这题的数据量比较大,一开始可以模拟一下过程,但是直接暴力肯定是超时 这题的数据量比较大,一开始可以模拟一下过程,但是直接暴力肯定是超时
 的,因为每次插入过程,这个位置的后面的元素必然是要顺序往后移动的。所以 的,因为每次插入过程,这个位置的后面的元素必然是要顺序往后移动的。所以
 总的复杂度高达O(n^2)。 总的复杂度高达O(n^2)。
 但是这个问题可以转化,我们这样考虑,对于任意两个整数对(A1,B1)和(A2,B2) 但是这个问题可以转化,我们这样考虑,对于任意两个整数对(A1,B1)和(A2,B2)
 保证(A1,B1)在(A2,B2)之前出现,如果A1小于A2,后面的整数对是不影响前面整 保证(A1,B1)在(A2,B2)之前出现,如果A1小于A2,后面的整数对是不影响前面整
 数对的位置关系的,否则B1的位置必然要受到B2的影响而向后移动一位。 数对的位置关系的,否则B1的位置必然要受到B2的影响而向后移动一位。
 于是A1和A2之间就存在一个逆序关系,我们可以联想到树状数组求逆序数时 于是A1和A2之间就存在一个逆序关系,我们可以联想到树状数组求逆序数时
 候的做法,从后往前,对于最后一个数,它的位置就是An,因为之后没有插入数 候的做法,从后往前,对于最后一个数,它的位置就是An,因为之后没有插入数
 了,它已经稳定下来了,然后将这个位置插入到树状数组的相应位置去,每次扫 了,它已经稳定下来了,然后将这个位置插入到树状数组的相应位置去,每次扫
 描到当前数的时候二分枚举当前数前面有多少“空位”,空位的统计可以采用树 描到当前数的时候二分枚举当前数前面有多少“空位”,空位的统计可以采用树
 状数组的成段求和,找到后将这个数插入,N次操作后答案就保存下来了。 状数组的成段求和,找到后将这个数插入,N次操作后答案就保存下来了。
 */ */

 #include <iostream> #include <iostream>

 using namespace std; using namespace std;

 #define maxn 200010 #define maxn 200010

 int n; int n;
 int c[maxn]; int c[maxn];

  struct point struct point  { {
 int A, B; int A, B;
 }pt[maxn]; }pt[maxn];

  int lowbit(int x) int lowbit(int x)  { {
 return x & (-x); return x & (-x);
 } }

  void add(int pos) void add(int pos)  { {
  while(pos <= n) while(pos <= n)  { {
 c[pos] ++; c[pos] ++;
 pos += lowbit(pos); pos += lowbit(pos);
 } }
 } }

  int sum(int pos) int sum(int pos)  { {
 int s = 0; int s = 0;
  while(pos > 0) while(pos > 0)  { {
 s += c[pos]; s += c[pos];
 pos -= lowbit(pos); pos -= lowbit(pos);
 } }
 return s; return s;
 } }

 int ans[maxn]; int ans[maxn];

  int main() int main()  { {
 int i; int i;
  while(scanf("%d", &n) != EOF) while(scanf("%d", &n) != EOF)  { {
 for(i = 1; i <= n; i++) for(i = 1; i <= n; i++)
 c[i] = 0; c[i] = 0;
  for(i = 1; i <= n; i++) for(i = 1; i <= n; i++)  { {
 scanf("%d %d", &pt[i].A, &pt[i].B); scanf("%d %d", &pt[i].A, &pt[i].B);
 pt[i].A ++; pt[i].A ++;
 } }
  for(i = n; i >= 1; i--) for(i = n; i >= 1; i--)  { {
 int l = 1; int l = 1;
 int r = n; int r = n;
 int as = 1; int as = 1;
  while(l <= r) while(l <= r)  { {
 int m = (l + r) >> 1; int m = (l + r) >> 1;
  if(m - sum(m) >= pt[i].A) if(m - sum(m) >= pt[i].A)  { {
 r = m - 1; r = m - 1;
 as = m; as = m;
 }else }else
 l = m + 1; l = m + 1;
 } }
 ans[as] = pt[i].B; ans[as] = pt[i].B;
 add(as); add(as);
 } }
  for(i = 1; i <= n; i++) for(i = 1; i <= n; i++)  { {
 if(i != 1) if(i != 1)
 printf(" "); printf(" ");
 printf("%d", ans[i]); printf("%d", ans[i]);
 } }
 puts(""); puts("");
 } }
 return 0; return 0;
 } }
摘要: 题目链接:http://poj.org/problem?id=2637
/**//*题意: 给定N(N <= 50000)条信息,表示第yi年的降水量是ri,然后给出M(M <= 10000)条询问,每条询问的格式是Y X,表示自从第Y年以来X这一年是最大的降水量,问这句话正确与否。&nb... 阅读全文
题目链接:http://poj.org/problem?id=3067
  /**//* /**//*
 题意: 题意:
 左边N个点,右边M个点,分别南北方向排列,1对应1,2对应2,给出 左边N个点,右边M个点,分别南北方向排列,1对应1,2对应2,给出
 K条记录,每条记录表示左边的A点和右边的B点相连,两条相连的先会有一 K条记录,每条记录表示左边的A点和右边的B点相连,两条相连的先会有一
 个交点,现在保证任意三个线不会交与一点,问一共多少个交点。 个交点,现在保证任意三个线不会交与一点,问一共多少个交点。

 题解: 题解:
 树状数组 树状数组

 思路: 思路:
 题目求的是交点的数目,仔细观察就可以发现,如果有以下四个点,A1 题目求的是交点的数目,仔细观察就可以发现,如果有以下四个点,A1
 ,B1属于左边,A2,B2属于右边,当且仅当 A1和A2的大小关系 和 B1与B2 ,B1属于左边,A2,B2属于右边,当且仅当 A1和A2的大小关系 和 B1与B2
 的大小关系 相反,于是可以联想到求一个数列的逆序数的时候用到的树状数 的大小关系 相反,于是可以联想到求一个数列的逆序数的时候用到的树状数
 组的成段求和。 组的成段求和。
 我们只要将读入的整数对按左边的点递增排序,如果左边点大小相同则按 我们只要将读入的整数对按左边的点递增排序,如果左边点大小相同则按
 右边点递增排序,每次在树状数组中统计比当前右边的点大的数的数目,然后 右边点递增排序,每次在树状数组中统计比当前右边的点大的数的数目,然后
 再将这个点插入树状数组,这就实现了一个逆序统计。 再将这个点插入树状数组,这就实现了一个逆序统计。
 这里需要注意的是,统计的时候需要采用__int64,因为总的交点数可能 这里需要注意的是,统计的时候需要采用__int64,因为总的交点数可能
 会超过int。最大的情况是左右两边都是1000个点,并且两两有边,那么最大 会超过int。最大的情况是左右两边都是1000个点,并且两两有边,那么最大
 的交点数量就是: 的交点数量就是:
 1 * (1 + 2 + 1 * (1 + 2 +  + 999) + 999)
 + +
 2 * (1 + 2 + 2 * (1 + 2 +  + 998) + 998)
 + +
 
 998 * (1 + 2) 998 * (1 + 2)
 + +
 999 * 1 999 * 1
 + +
 1000 * 0 1000 * 0
 可以写个程序统计一下,发现这个数字是超过int的。 可以写个程序统计一下,发现这个数字是超过int的。
 ll ans = 0; ll ans = 0;
 for(i = 1; i <= 1000; i++) { for(i = 1; i <= 1000; i++) {
 ans += i * (1001 - i) * (1000 - i) / 2; ans += i * (1001 - i) * (1000 - i) / 2;
 } }
 */ */


 #include <iostream> #include <iostream>
 #include <algorithm> #include <algorithm>

 using namespace std; using namespace std;

  struct Double struct Double  { {
 int l, r; int l, r;
 }dt[1000100]; }dt[1000100];

 int N, M, K; int N, M, K;
 #define ll __int64 #define ll __int64

  int cmp(Double a, Double b) int cmp(Double a, Double b)  { {
 if(a.l == b.l) if(a.l == b.l)
 return a.r < b.r; return a.r < b.r;
 return a.l < b.l; return a.l < b.l;
 } }

  int lowbit(int x) int lowbit(int x)  { {
 return x & (-x); return x & (-x);
 } }

 ll c[1010]; ll c[1010];
  void add(int pos) void add(int pos)  { {
  while(pos <= M) while(pos <= M)  { {
 c[pos] ++; c[pos] ++;
 pos += lowbit(pos); pos += lowbit(pos);
 } }
 } }

  ll sum(int pos) ll sum(int pos)  { {
 ll s = 0; ll s = 0;
  while(pos > 0) while(pos > 0)  { {
 s += c[pos]; s += c[pos];
 pos -= lowbit(pos); pos -= lowbit(pos);
 } }
 return s; return s;
 } }

  int main() int main()  { {
 int t; int t;
 int i; int i;
 int Case = 1; int Case = 1;




 scanf("%d", &t); scanf("%d", &t);

  while(t--) while(t--)  { {
 memset(c, 0, sizeof(c)); memset(c, 0, sizeof(c));
 scanf("%d %d %d", &N, &M, &K); scanf("%d %d %d", &N, &M, &K);
  for(i = 0; i < K; i++) for(i = 0; i < K; i++)  { {
 scanf("%d %d", &dt[i].l, &dt[i].r); scanf("%d %d", &dt[i].l, &dt[i].r);
 } }
 sort(dt, dt + K, cmp); sort(dt, dt + K, cmp);

 ll ans = 0; ll ans = 0;
  for(i = 0; i < K; i++) for(i = 0; i < K; i++)  { {
 ans += sum(M) - sum(dt[i].r); ans += sum(M) - sum(dt[i].r);
 add(dt[i].r); add(dt[i].r);
 } }
 printf("Test case %d: %I64d\n", Case++, ans); printf("Test case %d: %I64d\n", Case++, ans);
 } }
 return 0; return 0;
 } }


摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2871
/**//*题意: 现在有1到N(N <= 50000)个连续内存块,然后给出四种操作:1. Reset 释放所有内存块,并且输出“Reset Now”。2... 阅读全文
摘要: 题目链接:http://poj.org/problem?id=2720
/**//*题意: 给定三个整数 b, n, 和 i, 定义函数 f(x) = b^f(x-1) 如果 x > 0, 并且 f(0)=... 阅读全文
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=1166
  /**//* /**//*
 题意: 题意:
 给定N(N <= 50000)个数, 表示敌人有N个工兵营地,接下来有N个正整数, 第 给定N(N <= 50000)个数, 表示敌人有N个工兵营地,接下来有N个正整数, 第
 i个正整数ai代表第i个工兵营地里开始时有ai个人(1<=ai<=50)。 i个正整数ai代表第i个工兵营地里开始时有ai个人(1<=ai<=50)。
 接下来每行有一条命令,命令有4种形式: 接下来每行有一条命令,命令有4种形式:
 (1)Add i j ,i和j为正整数, 表示第i个营地增加j个人(j不超过30) (1)Add i j ,i和j为正整数, 表示第i个营地增加j个人(j不超过30)
 (2)Sub i j ,i和j为正整数, 表示第i个营地减少j个人(j不超过30); (2)Sub i j ,i和j为正整数, 表示第i个营地减少j个人(j不超过30);
 (3)Query i j ,i和j为正整数, i<=j,表示询问第i到第j个营地的总人数; (3)Query i j ,i和j为正整数, i<=j,表示询问第i到第j个营地的总人数;
 (4)End 表示结束,这条命令在每组数据最后出现 (4)End 表示结束,这条命令在每组数据最后出现

 解法: 解法:
 树状数组 或者 线段树 树状数组 或者 线段树

 思路: 思路:
 典型的树状数组模板题,Add和Sub是同一个操作,Sub就是Add一个负的值,只 典型的树状数组模板题,Add和Sub是同一个操作,Sub就是Add一个负的值,只
 是Sub之前先要判断这个点有没有这么多,询问就是利用树状数组的成段求和。 是Sub之前先要判断这个点有没有这么多,询问就是利用树状数组的成段求和。
 */ */

 #include <iostream> #include <iostream>

 using namespace std; using namespace std;

 #define maxn 1000010 #define maxn 1000010

 int c[maxn], n; int c[maxn], n;
 int a[maxn]; int a[maxn];
 char ch[100]; char ch[100];

  int lowbit(int x) int lowbit(int x)  { {
 return x & (-x); return x & (-x);
 } }

  void Add(int x, int add) void Add(int x, int add)  { {
  while(x <= n) while(x <= n)  { {
 c[x] += add; c[x] += add;
 x += lowbit(x); x += lowbit(x);
 } }
 } }

  int sum(int x) int sum(int x)  { {
 int s = 0; int s = 0;
  while(x > 0) while(x > 0)  { {
 s += c[x]; s += c[x];
 x -= lowbit(x); x -= lowbit(x);
 } }
 return s; return s;
 } }

  int main() int main()  { {
 int t, as, bs, i, q = 1; int t, as, bs, i, q = 1;
 scanf("%d", &t); scanf("%d", &t);
  while(t--) while(t--)  { {
 scanf("%d", &n); scanf("%d", &n);
 memset(c, 0, sizeof(c)); memset(c, 0, sizeof(c));
  for(i = 1; i <= n ;i++) for(i = 1; i <= n ;i++)  { {
 scanf("%d", &a[i]); scanf("%d", &a[i]);
 Add(i, a[i]); Add(i, a[i]);
 } }
 printf("Case %d:\n", q++); printf("Case %d:\n", q++);
  while(scanf("%s" , ch) != EOF) while(scanf("%s" , ch) != EOF)  { {
 if(!strcmp(ch, "End")) if(!strcmp(ch, "End"))
 break; break;
  else if(!strcmp(ch, "Query")) else if(!strcmp(ch, "Query"))  { {
 scanf("%d%d", &as, &bs); scanf("%d%d", &as, &bs);
 printf("%d\n", sum(bs) - sum(as - 1)); printf("%d\n", sum(bs) - sum(as - 1));
  }else if(!strcmp(ch, "Add")) }else if(!strcmp(ch, "Add"))  { {
 scanf("%d%d", &as, &bs); scanf("%d%d", &as, &bs);
 Add(as, bs); Add(as, bs);
  } else if(!strcmp(ch, "Sub")) } else if(!strcmp(ch, "Sub"))  { {
 scanf("%d%d", &as, &bs); scanf("%d%d", &as, &bs);
 Add(as, -bs); Add(as, -bs);
 } }
 } }

 } }
 } }
题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=1484
  /**//* /**//*
 题意: 题意:
 给出0 ~ N-1 (1 <= N <= 5000) 的一个排列, 经过循环移位,一共有N个排列, 给出0 ~ N-1 (1 <= N <= 5000) 的一个排列, 经过循环移位,一共有N个排列,
 问这N个排列中逆序对数目最小的。 问这N个排列中逆序对数目最小的。

 解法: 解法:
 树状数组 树状数组

 思路: 思路:
 树状数组求逆序数有一个经典算法,把数字大小对应到树状数组的小标,然后 树状数组求逆序数有一个经典算法,把数字大小对应到树状数组的小标,然后
 从后往前遍历每个数字,统计比这个数字小的数的个数,然后将这个数插入到树状 从后往前遍历每个数字,统计比这个数字小的数的个数,然后将这个数插入到树状
 数组中,遍历完毕,累加和就是该序列的逆序对的数目。 数组中,遍历完毕,累加和就是该序列的逆序对的数目。
 这题要求序列循环移位n次,每次移位统计一次逆序对,最后得到最小的,如果 这题要求序列循环移位n次,每次移位统计一次逆序对,最后得到最小的,如果
 按照前面的算法,最好的情况是O(n^2log(n)),所以需要找到一些技巧,将复杂度 按照前面的算法,最好的情况是O(n^2log(n)),所以需要找到一些技巧,将复杂度
 降下来,我们发现以下两个数列: 降下来,我们发现以下两个数列:
 1. a1, a2, 1. a1, a2,  , an-1, an , an-1, an
 2. a2, a3, 2. a2, a3,  , an, a1 , an, a1
 第二个是第一个循环左移一位的结果,如果将第一个序列的逆序数分情况讨论就是 第二个是第一个循环左移一位的结果,如果将第一个序列的逆序数分情况讨论就是
 S = A + B;其中A = (a2~an)本身的逆序对数目;B = a1和(a2~an)的逆序对数目; S = A + B;其中A = (a2~an)本身的逆序对数目;B = a1和(a2~an)的逆序对数目;
 而第二个序列中则是S' = A + B';其中B' = (n-1) - B,于是S和A如果已知,那么 而第二个序列中则是S' = A + B';其中B' = (n-1) - B,于是S和A如果已知,那么
 就可以轻松求得S' = A + (n-1) - (S - A)。这样一来,只要知道前一个序列的逆 就可以轻松求得S' = A + (n-1) - (S - A)。这样一来,只要知道前一个序列的逆
 序数,下一个序列就可以在O(1)的时间内求得。只要每次更新S 和 A 的值即可。 序数,下一个序列就可以在O(1)的时间内求得。只要每次更新S 和 A 的值即可。
 更加一般化的,S表示当前序列的逆序数对数,A表示比当前数小的数的个数, 更加一般化的,S表示当前序列的逆序数对数,A表示比当前数小的数的个数,
 题目中数列是一个排列,所以A的值其实就是当前值减一。 题目中数列是一个排列,所以A的值其实就是当前值减一。
 */ */

 #include <iostream> #include <iostream>
 #include <cstdio> #include <cstdio>
 #include <cstring> #include <cstring>
 using namespace std; using namespace std;

 #define maxn 5001 #define maxn 5001

 int n; int n;
 short c[maxn], val[maxn]; short c[maxn], val[maxn];

  int lowbit(int x) int lowbit(int x)  { {
 return x & (-x); return x & (-x);
 } }

  void add(int pos) void add(int pos)  { {
  while(pos <= n) while(pos <= n)  { {
 c[pos] ++; c[pos] ++;
 pos += lowbit(pos); pos += lowbit(pos);
 } }
 } }

  int sum(int pos) int sum(int pos)  { {
 int s = 0; int s = 0;
  while(pos > 0) while(pos > 0)  { {
 s += c[pos]; s += c[pos];
 pos -= lowbit(pos); pos -= lowbit(pos);
 } }
 return s; return s;
 } }

  int main() int main()  { {
 int i; int i;
  while(scanf("%d", &n) != EOF) while(scanf("%d", &n) != EOF)  { {
  for(i = 1; i <= n; i++) for(i = 1; i <= n; i++)  { {
 int x; int x;
 scanf("%d", &x); scanf("%d", &x);
 val[i] = x + 1; val[i] = x + 1;
 } }
 for(i = 1; i <= n; i++) for(i = 1; i <= n; i++)
 c[i] = 0; c[i] = 0;
 int ans = 0; int ans = 0;
  for(i = n; i >= 1; i--) for(i = n; i >= 1; i--)  { {
 int x = sum(val[i] - 1); int x = sum(val[i] - 1);
 add(val[i]); add(val[i]);
 ans += x; ans += x;
 } }

 int Min = ans; int Min = ans;
 int A = val[1] - 1; int A = val[1] - 1;
  for(i = 2; i <= n; i++) for(i = 2; i <= n; i++)  { {
 ans = ans - A + (n-1-A); ans = ans - A + (n-1-A);
 A = val[i] - 1; A = val[i] - 1;
 if(ans < Min) if(ans < Min)
 Min = ans; Min = ans;
 } }
 printf("%d\n", Min); printf("%d\n", Min);
 } }
 return 0; return 0;
 } }
摘要: 题目链接:http://poj.org/problem?id=3378
/**//*题意: 给定N (1 <= N <= 50000) 个小于等于10^9的数Ai, 要求找出Crazy Thair的数量。Crazy Thair是一个五元组{i,&nb... 阅读全文
摘要: 题目链接:http://poj.org/problem?id=2892
/**//*题意: 给出M(M <= 50000)组操作,每组操作的形式如下:1 D x: 将第x个村庄摧毁2 Q x: 询问和第x个村庄直接或者间接连接的村庄数目3 R: ... 阅读全文
题目链接: http://poj.org/problem?id=2155
  /**//* /**//*
 题意: 题意:
 对于一个n*n(n <= 1000)的矩阵A,要求作如下操作: 对于一个n*n(n <= 1000)的矩阵A,要求作如下操作:
 1. C x1 y1 x2 y2 (1 <= x1 <= x2 <= n, 1 <= y1 <= y2 <= n) 将当前范围内 1. C x1 y1 x2 y2 (1 <= x1 <= x2 <= n, 1 <= y1 <= y2 <= n) 将当前范围内
 的值和1异或。 的值和1异或。
 2. Q x y (1 <= x, y <= n) 询问 A[x, y]。 2. Q x y (1 <= x, y <= n) 询问 A[x, y]。

 解法: 解法:
 树状数组 树状数组

 思路: 思路:
 这题和树状数组的操作正好相反,树状数组是对点更新,成段求和,这题要 这题和树状数组的操作正好相反,树状数组是对点更新,成段求和,这题要
 求成段更新,对点求值。但是还是可以转化,我们不妨先来考虑一维的情况,给 求成段更新,对点求值。但是还是可以转化,我们不妨先来考虑一维的情况,给
 定一排数字,每次在区间进行进行成端加上一个数,然后询问某个点的值,很容 定一排数字,每次在区间进行进行成端加上一个数,然后询问某个点的值,很容
 易想到线段树,但是线段树的常系数太大,我们试图用树状数组来解决,方法是 易想到线段树,但是线段树的常系数太大,我们试图用树状数组来解决,方法是
 给定区间[a, b],如果要求在[a,b]区间都加上T我们只要在a的位置插入一个T, 给定区间[a, b],如果要求在[a,b]区间都加上T我们只要在a的位置插入一个T,
 然后在b+1的位置插入一个-T,这样下次询问某个值k的时候,只要将[1,k]的和求 然后在b+1的位置插入一个-T,这样下次询问某个值k的时候,只要将[1,k]的和求
 出来就是k这个位置的值,为什么呢?分三种情况讨论: 出来就是k这个位置的值,为什么呢?分三种情况讨论:
 1. k < a 先前的插入操作不影响此次结果 1. k < a 先前的插入操作不影响此次结果
 2. a <= k <= b a的位置插入T后,统计时值被加了一次 2. a <= k <= b a的位置插入T后,统计时值被加了一次
 3. k > b。 a的位置有T,b+1的位置有-T,正好抵消 3. k > b。 a的位置有T,b+1的位置有-T,正好抵消
 所以结论成立。 所以结论成立。
 然后就可以扩展到二维的情况,也是一样,如果对于(x1, y1) (x2, y2)这个 然后就可以扩展到二维的情况,也是一样,如果对于(x1, y1) (x2, y2)这个
 矩形,只要在(x1, y1) (x2+1, y2+1)这两个点插入T,而(x2+1, y1) (x1, y2+1) 矩形,只要在(x1, y1) (x2+1, y2+1)这两个点插入T,而(x2+1, y1) (x1, y2+1)
 这两个点插入-T即可。 这两个点插入-T即可。
 本题的操作是异或,其实还是一样的,就是在二进制内的无进位加法。 本题的操作是异或,其实还是一样的,就是在二进制内的无进位加法。
 */ */

 #include <iostream> #include <iostream>

 using namespace std; using namespace std;

 #define maxn 1001 #define maxn 1001

 int c[maxn][maxn]; int c[maxn][maxn];
 int n; int n;

  int lowbit(int x) int lowbit(int x)  { {
 return x & (-x); return x & (-x);
 } }

  void add(int x, int y) void add(int x, int y)  { {
  while(x <= n) while(x <= n)  { {
 int ty = y; int ty = y;
  while(ty <= n) while(ty <= n)  { {
 c[x][ty] ^= 1; c[x][ty] ^= 1;
 ty += lowbit(ty); ty += lowbit(ty);
 } }
 x += lowbit(x); x += lowbit(x);
 } }
 } }

  int sum(int x, int y) int sum(int x, int y)  { {
 int s = 0; int s = 0;
 if(x > n) x = n; if(x > n) x = n;
 if(y > n) y = n; if(y > n) y = n;
  while(x >= 1) while(x >= 1)  { {
 int ty = y; int ty = y;
  while(ty >= 1) while(ty >= 1)  { {
 s ^= c[x][ty]; s ^= c[x][ty];
 ty -= lowbit(ty); ty -= lowbit(ty);
 } }
 x -= lowbit(x); x -= lowbit(x);
 } }
 return s; return s;
 } }


  int main() int main()  { {
 int t, m; int t, m;
 int i, j; int i, j;
 scanf("%d", &t); scanf("%d", &t);

  while(t--) while(t--)  { {
 scanf("%d %d", &n, &m); scanf("%d %d", &n, &m);
 memset(c, 0, sizeof(c)); memset(c, 0, sizeof(c));
  while(m--) while(m--)  { {
 char str[5]; char str[5];
 int x1, y1, x2, y2; int x1, y1, x2, y2;
 scanf("%s", str); scanf("%s", str);
  if(str[0] == 'C') if(str[0] == 'C')  { {
 scanf("%d %d %d %d", &x1, &y1, &x2, &y2); scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
 add(x1, y1); add(x1, y1);
 add(x2+1, y2+1); add(x2+1, y2+1);
 add(x1, y2+1); add(x1, y2+1);
 add(x2+1, y1); add(x2+1, y1);
  }else }else  { {
 scanf("%d %d", &x1, &y1); scanf("%d %d", &x1, &y1);
 printf( "%d\n", sum(x1, y1) ); printf( "%d\n", sum(x1, y1) );
 } }
 } }

 if(t) if(t)
 puts(""); puts("");
 } }
 return 0; return 0;
 } }

摘要: 题目链接:http://poj.org/problem?id=2886
/**//*题意: 有一排编号为1到N的小孩顺时针围成圈,没人手上有一张编号为A[i]的卡片,游戏从第K个小孩开始,他告诉自己的卡片数字然后跳出圆圈,如果A[i]大于0,那么左数第A[i]个小孩出圈否则右数第A[i]个出圈,游戏一直进行直到所有孩子都出去位置,第p个出圈的将会得到... 阅读全文
题目链接:http://poj.org/problem?id=2985
  /**//* /**//*
 题意: 题意:
 给定N(N <= 200000)个操作,每个操作是以下两种形式: 给定N(N <= 200000)个操作,每个操作是以下两种形式:
 0 x y : 合并x所在的组和y所在的组,如果x和y同组,不合并。 0 x y : 合并x所在的组和y所在的组,如果x和y同组,不合并。
 1 k:输出第k大的组的元素个数。 1 k:输出第k大的组的元素个数。

 解法: 解法:
 树状数组 + 并查集 树状数组 + 并查集

 思路: 思路:
 将元素的个数对应树状数组的下标,每次合并操作,在树状 将元素的个数对应树状数组的下标,每次合并操作,在树状
 数组中对应两个集合大小的位置分别减1,两集合之后的位置+1, 数组中对应两个集合大小的位置分别减1,两集合之后的位置+1,
 询问操作只需要二分答案,然后每次统计比k大的数的个数判可行 询问操作只需要二分答案,然后每次统计比k大的数的个数判可行
 即可。 即可。
 */ */

 #include <iostream> #include <iostream>

 using namespace std; using namespace std;

 #define maxn 200010 #define maxn 200010

 int c[maxn]; int c[maxn];
 int prev[maxn], num[maxn]; int prev[maxn], num[maxn];
 int n; int n;

  int lowbit(int x) int lowbit(int x)  { {
 return x & (-x); return x & (-x);
 } }
  void add(int pos, int num) void add(int pos, int num)  { {
  while(pos <= n) while(pos <= n)  { {
 c[pos] += num; c[pos] += num;
 pos += lowbit(pos); pos += lowbit(pos);
 } }
 } }

  int sum(int pos) int sum(int pos)  { {
 int s = 0; int s = 0;
  while(pos > 0) while(pos > 0)  { {
 s += c[pos]; s += c[pos];
 pos -= lowbit(pos); pos -= lowbit(pos);
 } }
 return s; return s;
 } }

  int find(int x) int find(int x)  { {
 int q = x; int q = x;
  while(x != prev[x]) while(x != prev[x])  { {
 x = prev[x]; x = prev[x];
 } }
 return x; return x;
 } }

  void Union(int x, int y) void Union(int x, int y)  { {
 x = find(x); x = find(x);
 y = find(y); y = find(y);

  if(x != y) if(x != y)  { {
 if(num[x] == num[y]) if(num[x] == num[y])
 add(num[x], -2); add(num[x], -2);
  else else  { {
 add(num[x], -1); add(num[x], -1);
 add(num[y], -1); add(num[y], -1);
 } }
 add(num[x] + num[y], 1); add(num[x] + num[y], 1);

  if(num[x] < num[y]) if(num[x] < num[y])  { {
 prev[x] = y; prev[x] = y;
 num[y] += num[x]; num[y] += num[x];
  }else }else  { {
 prev[y] = x; prev[y] = x;
 num[x] += num[y]; num[x] += num[y];
 } }
 } }
 } }


  int Query(int k) int Query(int k)  { {
 int l = 1; int l = 1;
 int r = n; int r = n;
 int ans = 0; int ans = 0;
 int all = sum(n); int all = sum(n);
  while(l <= r) while(l <= r)  { {
 int m = (l + r) >> 1; int m = (l + r) >> 1;
  if(k <= all - sum(m-1)) if(k <= all - sum(m-1))  { {
 l = m + 1; l = m + 1;
 ans = m; ans = m;
 }else }else
 r = m - 1; r = m - 1;
 } }
 return ans; return ans;
 } }

  int main() int main()  { {
 int i, m; int i, m;
 int op, x, y; int op, x, y;
  while(scanf("%d %d", &n, &m) != EOF) while(scanf("%d %d", &n, &m) != EOF)  { {
  for(i = 1; i <= n; i++) for(i = 1; i <= n; i++)  { {
 c[i] = 0; c[i] = 0;
 prev[i] = i; prev[i] = i;
 num[i] = 1; num[i] = 1;
 } }
 add(1, n); add(1, n);
  while(m--) while(m--)  { {
 scanf("%d", &op); scanf("%d", &op);
  if(op == 0) if(op == 0)  { {
 scanf("%d %d", &x, &y); scanf("%d %d", &x, &y);
 Union(x, y); Union(x, y);
  }else }else  { {
 scanf("%d", &x); scanf("%d", &x);
 printf("%d\n", Query(x)); printf("%d\n", Query(x));
 } }
 } }

 } }
 return 0; return 0;
 } }
摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3450
/**//*题意: 给定N(N <= 100000)个数字ai和一个H,要求求出特殊序列的数量,所谓特殊序列,就是相邻两个数字的绝对值小于等于H并且序列长度大于等于2。解法:树状数组 + 动态规划思路:... 阅读全文
摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2836
/**//*题意: 给定N(N <= 100000)个数字ai和一个H,要求求出特殊序列的数量,所谓特殊序列,就是相邻两个数字的绝对值小于等于H并且序列长度大于等于2。解法:树状数组 + 动态规划思路:... 阅读全文
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2227
  /**//* /**//*
 题意: 题意:
 给定N(N <= 100000)个数字ai,找出这个序列中有多少非递减序列。 给定N(N <= 100000)个数字ai,找出这个序列中有多少非递减序列。

 解法: 解法:
 树状数组 + 动态规划 树状数组 + 动态规划

 思路: 思路:
 如果n的值小于等于1000,我们可以用动态规划来解,dp[i]表示 如果n的值小于等于1000,我们可以用动态规划来解,dp[i]表示
 到第i个位置能够找到的非递减序列的解的数量,那么有状态转移方程 到第i个位置能够找到的非递减序列的解的数量,那么有状态转移方程
 dp[i] = sum{ dp[j], j<i, a[j]<=a[i] },这个时间复杂度是O(n^2) dp[i] = sum{ dp[j], j<i, a[j]<=a[i] },这个时间复杂度是O(n^2)
 ,但是n很大,所以不能采用,但是我们观察到这个转移方程是以求和 ,但是n很大,所以不能采用,但是我们观察到这个转移方程是以求和
 的形式出现,并且有一个限制条件就是a[j] <= a[i],那么如果我们把 的形式出现,并且有一个限制条件就是a[j] <= a[i],那么如果我们把
 数字映射到下标,就可以轻松的通过树状数组的成段求和来统计了。 数字映射到下标,就可以轻松的通过树状数组的成段求和来统计了。
 具体做法是:由于数字较大,我们可以先将所有数字离散化,这样 具体做法是:由于数字较大,我们可以先将所有数字离散化,这样
 每个数字就有一个 <= n 的标号,然后这个标号就可以对应树状数组的 每个数字就有一个 <= n 的标号,然后这个标号就可以对应树状数组的
 下标了,每次从左往右在树状数组中统计比当前数小或者相等的数的个 下标了,每次从左往右在树状数组中统计比当前数小或者相等的数的个
 数,然后将当前数字(离散后的数字)插入到树状数组中,循环结束, 数,然后将当前数字(离散后的数字)插入到树状数组中,循环结束,
 累加和就是最后的答案了。 累加和就是最后的答案了。
 。 。
 */ */

 #include <iostream> #include <iostream>
 #include <cstdio> #include <cstdio>
 #include <cstring> #include <cstring>
 #include <algorithm> #include <algorithm>
 using namespace std; using namespace std;

 typedef unsigned int ui; typedef unsigned int ui;
 typedef __int64 ll; typedef __int64 ll;

 #define maxn 100010 #define maxn 100010
 #define mod 1000000007 #define mod 1000000007

 int n; int n;
 ui val[maxn], t[maxn]; ui val[maxn], t[maxn];
 ll c[maxn]; ll c[maxn];
 int tot; int tot;

  int lowbit(int x) int lowbit(int x)  { {
 return x & (-x); return x & (-x);
 } }

  void add(int pos, ll v) void add(int pos, ll v)  { {
  while(pos <= tot) while(pos <= tot)  { {
 c[pos] += v; if(c[pos] >= mod ) c[pos] %= mod; c[pos] += v; if(c[pos] >= mod ) c[pos] %= mod;
 pos += lowbit(pos); pos += lowbit(pos);
 } }
 } }

  ll sum(int pos) ll sum(int pos)  { {
 int s = 0; int s = 0;
  while(pos >= 1) while(pos >= 1)  { {
 s += c[pos]; if(s >= mod ) s %= mod; s += c[pos]; if(s >= mod ) s %= mod;
 pos -= lowbit(pos); pos -= lowbit(pos);
 } }
 return s; return s;
 } }

  int Bin(ui v) int Bin(ui v)  { {
 int l = 1; int l = 1;
 int r = tot; int r = tot;
  while(l <= r) while(l <= r)  { {
 int m = (l + r) >> 1; int m = (l + r) >> 1;
 if(v == t[m]) if(v == t[m])
 return m; return m;
 if(v > t[m]) if(v > t[m])
 l = m + 1; l = m + 1;
 else else
 r = m - 1; r = m - 1;
 } }
 } }

  int main() int main()  { {
 int i; int i;
  while(scanf("%d", &n) != EOF) while(scanf("%d", &n) != EOF)  { {
  for(i = 0; i < n; i++) for(i = 0; i < n; i++)  { {
 scanf("%u", &val[i]); scanf("%u", &val[i]);
 t[i+1] = val[i]; t[i+1] = val[i];
 } }
 tot = 0; tot = 0;
 sort(t+1, t+1+n); sort(t+1, t+1+n);
  for(i = 1; i <= n; i++) for(i = 1; i <= n; i++)  { {
  if(i==1 || t[i] != t[i-1]) if(i==1 || t[i] != t[i-1])  { {
 t[++tot] = t[i]; t[++tot] = t[i];
 c[tot] = 0; c[tot] = 0;
 } }
 } }
  for(i = 0; i < n; i++) for(i = 0; i < n; i++)  { {
 val[i] = Bin(val[i]); val[i] = Bin(val[i]);
 } }
 ll ans = 0; ll ans = 0;
 add(1, 1); add(1, 1);
  for(i = 0; i < n; i++) for(i = 0; i < n; i++)  { {
 ll x = sum(val[i]); ll x = sum(val[i]);
 ans += x; if(ans >= mod) ans %= mod; ans += x; if(ans >= mod) ans %= mod;
 add(val[i], x); add(val[i], x);
 } }
 printf("%d\n", (int)ans); printf("%d\n", (int)ans);
 } }
 return 0; return 0;
 } }
题目链接:http://poj.org/problem?id=3492
  /**//* /**//*
 题意: 题意:
 给出n(n <= 500)个数ai(ai <= 5000),求他们的最大不能组合数。 给出n(n <= 500)个数ai(ai <= 5000),求他们的最大不能组合数。

 解法: 解法:
 数论 + 最短路 数论 + 最短路

 思路: 思路:
 经典的组合问题Change Making Problem,这个题目有一个限制就是给 经典的组合问题Change Making Problem,这个题目有一个限制就是给
 定的数小于等于5000,题目的意思很清楚,就是求一个数S,使得它不能被 定的数小于等于5000,题目的意思很清楚,就是求一个数S,使得它不能被
 任何ai的倍数所组合出来,并且它的值最大。 任何ai的倍数所组合出来,并且它的值最大。
 那么如果这n个数的gcd不为1,必然找不到这样的S,因为如果S不能被 那么如果这n个数的gcd不为1,必然找不到这样的S,因为如果S不能被
 它们的gcd整除,永远不可能组合出来,这样S就可以很大,自然也就没有最 它们的gcd整除,永远不可能组合出来,这样S就可以很大,自然也就没有最
 大的S了。 大的S了。
 现在讨论所有ai的gcd为1的情况。对于任意的整数A,如果A能被以上的 现在讨论所有ai的gcd为1的情况。对于任意的整数A,如果A能被以上的
 ai组合出来,那么 B = A + k*a0 必然能被组合(只要加上k个a0即可)。于 ai组合出来,那么 B = A + k*a0 必然能被组合(只要加上k个a0即可)。于
 是我们可以吧所有整数划分成a0个等价类,等价类中的数模a0的值相同,举 是我们可以吧所有整数划分成a0个等价类,等价类中的数模a0的值相同,举
 个例子,a0=3,我们可以将0,1,2,3,4,5,6划分成(0,3,6)(1,4)(2,5)这三个 个例子,a0=3,我们可以将0,1,2,3,4,5,6划分成(0,3,6)(1,4)(2,5)这三个
 等价类,如果相同等价类中的某个数能被组合,那么比它大的所有在该等价 等价类,如果相同等价类中的某个数能被组合,那么比它大的所有在该等价
 类中的数必然能被组合出来。所以现在只要求出每个等价类中的最小的能被 类中的数必然能被组合出来。所以现在只要求出每个等价类中的最小的能被
 组合出来的数,然后取所有等价类中最小数的最大值L,L-a[0]就是问题的 组合出来的数,然后取所有等价类中最小数的最大值L,L-a[0]就是问题的
 答案(原因很简单,因为L能被组合出来,比L大的并且在同一等价类中的数 答案(原因很简单,因为L能被组合出来,比L大的并且在同一等价类中的数
 必然能通过加上若干个a[0]来求得,于是L-a[0]就成了最大不能组合数)。 必然能通过加上若干个a[0]来求得,于是L-a[0]就成了最大不能组合数)。
 于是问题就转化成了如何在相同等价类中找到最小的那个能被ai组合出 于是问题就转化成了如何在相同等价类中找到最小的那个能被ai组合出
 来的数。可以利用最短路来求,最短路的key信息就是它本身值的大小,如果 来的数。可以利用最短路来求,最短路的key信息就是它本身值的大小,如果
 两个数x,y, (x + ai) % a0 == y % a0,那么我们就在x和y之前连上一条权 两个数x,y, (x + ai) % a0 == y % a0,那么我们就在x和y之前连上一条权
 值为ai的边,构图完成后就可以从0这个点开始搜了,最后遍历0到a[0]-1找 值为ai的边,构图完成后就可以从0这个点开始搜了,最后遍历0到a[0]-1找
 到最大的那个数L即可。 到最大的那个数L即可。
 */ */

 #include <iostream> #include <iostream>
 #include <algorithm> #include <algorithm>
 #include <queue> #include <queue>
 using namespace std; using namespace std;

 #define maxn 5010 #define maxn 5010
 #define inf 200000000 #define inf 200000000

 int a[500]; int a[500];

  struct Point struct Point  { {
 int val; int val;
 int mod_val; int mod_val;
 int dis; int dis;
  Point(int _v, int _mv, int _d) Point(int _v, int _mv, int _d)  { {
 val = _v; val = _v;
 mod_val = _mv; mod_val = _mv;
 dis = _d; dis = _d;
 } }
  friend bool operator < (Point a, Point b) friend bool operator < (Point a, Point b)  { {
 return a.dis > b.dis; return a.dis > b.dis;
 } }
 }; };

 int dis[maxn], nv[maxn]; int dis[maxn], nv[maxn];
 priority_queue < Point > Q; priority_queue < Point > Q;



  int gcd(int a, int b) int gcd(int a, int b)  { {
 if(b == 0) if(b == 0)
 return a; return a;
 return gcd(b, a%b); return gcd(b, a%b);
 } }

  int main() int main()  { {
 int n; int n;
 int i; int i;
  while(scanf("%d", &n) != EOF) while(scanf("%d", &n) != EOF)  { {
 int G = 0; int G = 0;
  for(i = 0; i < n; i++) for(i = 0; i < n; i++)  { {
 scanf("%d", &a[i]); scanf("%d", &a[i]);
 if(!i) if(!i)
 G = a[0]; G = a[0];
 else else
 G = gcd(G, a[i]); G = gcd(G, a[i]);
 } }
  if(G != 1) if(G != 1)  { {
 printf("INF\n"); printf("INF\n");
 continue; continue;
 } }

 sort(a, a + n); sort(a, a + n);
  for(i = 0; i < a[0]; i++) for(i = 0; i < a[0]; i++)  { {
 dis[i] = inf; dis[i] = inf;
 } }
 dis[0] = 0; dis[0] = 0;
 nv[0] = 0; nv[0] = 0;
  while(!Q.empty()) while(!Q.empty())  { {
 Q.pop(); Q.pop();
 } }
 Q.push(Point(0, 0, 0)); Q.push(Point(0, 0, 0));

  while(!Q.empty()) while(!Q.empty())  { {
 Point id = Q.top(); Point id = Q.top();
 Q.pop(); Q.pop();
  for(i = 0; i < n; i++) for(i = 0; i < n; i++)  { {
 int nex = (id.mod_val + a[i]) % a[0]; int nex = (id.mod_val + a[i]) % a[0];
  if(id.dis + a[i] < dis[nex]) if(id.dis + a[i] < dis[nex])  { {
 dis[nex] = id.dis + a[i]; dis[nex] = id.dis + a[i];
 nv[nex] = id.val + a[i]; nv[nex] = id.val + a[i];
 Q.push(Point(nv[nex], nex, dis[nex])); Q.push(Point(nv[nex], nex, dis[nex]));
 } }
 } }
 } }
 int Max = 0; int Max = 0;
  for(i = 0; i < a[0]; i++) for(i = 0; i < a[0]; i++)  { {
  if(dis[i] != inf && nv[i] > Max) if(dis[i] != inf && nv[i] > Max)  { {
 Max = nv[i]; Max = nv[i];
 } }
 } }
 printf("%d\n", Max - a[0]); printf("%d\n", Max - a[0]);
 } }
 return 0; return 0;
 } }
摘要: 题目链接:http://poj.org/problem?id=3667
/**//*题意: 给出M(M <= 50000)组操作,每组操作的形式如下:1 D: 询问是否有长度为D的连续区间,如果存在输出最左边的,否则输出0,并且将这块连续的区间占据。2 X D:将从X开始的连续D块空间... 阅读全文
摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3706
/**//*题意: 给定N(N <= 100000)个点,要求找到任意一个点的最近点,点的距离定义如下:Distance (A, B) = max (|Ax &#... 阅读全文
摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1823
/**//*题意: 二维区间求最大值。解法:二维线段树 或者 二维RMQ思路: 一维线段树是一颗完全二叉树,那么二维线段树无疑就是一颗完全四叉树,换言之,每个结点有四个儿子,这里为了... 阅读全文
摘要: 题目链接:http://poj.org/problem?id=1177
/**//*题意: 给定N(N <= 5000)个矩形纸片,求它们重叠后外围轮廓的周长。解法:线段树思路: 矩形面积并的变形,其实只需要修改Update函数即可,在线段树的结点中保存一个nCover域,表示当... 阅读全文
摘要: 题目链接:http://poj.org/problem?id=3277
/**//*题意: 给定N(N <= 40000)个矩形,求它们的面积并。解法:离散化+线段树思路: 矩形面积并的nlog(n)经典算法。首先我们将每个矩形的纵向边投影到Y轴上,这样就可以把矩形的纵向边看成一... 阅读全文
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2795
  /**//* /**//*
 题意: 题意:
 对于w*h(w <= 10^9, h <= 10^9 )的一块区域,连续摆放1*wi的木板,木板不能 对于w*h(w <= 10^9, h <= 10^9 )的一块区域,连续摆放1*wi的木板,木板不能
 旋转,如果能放下就选择最靠上的位置摆放,并且输出行号,如果找不到直接输出-1。 旋转,如果能放下就选择最靠上的位置摆放,并且输出行号,如果找不到直接输出-1。

 解法: 解法:
 线段树 线段树

 思路: 思路:
 将h这一维映射到线段树的区间,w这一维则对应区间点上的最大值,每次询问时 将h这一维映射到线段树的区间,w这一维则对应区间点上的最大值,每次询问时
 做一次插入操作,如果当前访问的结点的最大值小于给定值,直接返回-1。否则,左 做一次插入操作,如果当前访问的结点的最大值小于给定值,直接返回-1。否则,左
 子树的最大值大于当前值,那么访问左子树,小于则访问右子树,直到叶子结点。如 子树的最大值大于当前值,那么访问左子树,小于则访问右子树,直到叶子结点。如
 果成功找到,说明给定值小于叶子结点的值,将叶子结点的值减去给定值,然后递归 果成功找到,说明给定值小于叶子结点的值,将叶子结点的值减去给定值,然后递归
 更新内部结点的最值。 更新内部结点的最值。
 */ */

 #include <iostream> #include <iostream>

 using namespace std; using namespace std;

 #define maxn 200010 #define maxn 200010

  struct Tree struct Tree  { {
 int Max; int Max;
 int root, l, r; int root, l, r;
 }T[maxn*4]; }T[maxn*4];

 int h, w, n; int h, w, n;
  void Build(int p, int l, int r) void Build(int p, int l, int r)  { {
 T[p].root = p; T[p].root = p;
 T[p].l = l; T[p].l = l;
 T[p].r = r; T[p].r = r;
 T[p].Max = w; T[p].Max = w;
  if(l == r) if(l == r)  { {
 return ; return ;
 } }
 int mid = (l + r) >> 1; int mid = (l + r) >> 1;
 Build(p<<1, l, mid); Build(p<<1, l, mid);
 Build(p<<1|1, mid+1, r); Build(p<<1|1, mid+1, r);
 } }

  int MMax(int a, int b) int MMax(int a, int b)  { {
 return a > b ? a : b; return a > b ? a : b;
 } }

  int Insert(int p, int val) int Insert(int p, int val)  { {
  if(T[p].l == T[p].r) if(T[p].l == T[p].r)  { {
 if(T[p].Max < val) if(T[p].Max < val)
 return -1; return -1;
 T[p].Max -= val; T[p].Max -= val;
 return T[p].l; return T[p].l;
 } }

  if(val <= T[p].Max) if(val <= T[p].Max)  { {
 int x = 0; int x = 0;
  if(val <= T[p<<1].Max) if(val <= T[p<<1].Max)  { {
 x = Insert(p<<1, val); x = Insert(p<<1, val);
  }else }else  { {
 x = Insert(p<<1|1, val); x = Insert(p<<1|1, val);
 } }
 T[p].Max = MMax(T[p<<1].Max, T[p<<1|1].Max); T[p].Max = MMax(T[p<<1].Max, T[p<<1|1].Max);
 return x; return x;
 }else }else
 return -1; return -1;
 } }

  int main() int main()  { {
 int i, X; int i, X;
  while(scanf("%d %d %d", &h, &w, &n) != EOF) while(scanf("%d %d %d", &h, &w, &n) != EOF)  { {
 if(h > n) if(h > n)
 h = n; h = n;

 Build(1, 1, h); Build(1, 1, h);
  for(i = 0; i < n; i++) for(i = 0; i < n; i++)  { {
 scanf("%d", &X); scanf("%d", &X);
 printf( "%d\n", Insert(1, X) ); printf( "%d\n", Insert(1, X) );
 } }
 } }
 return 0; return 0;
 } }
题目大意: 给出N(N <= 8000)条垂直线段,如果两条线段在水平方向上连一条线之后不和其他任何垂直线段相交,那么我们称这两条线段水平可见,如果三条垂直线段两两水平可见,则称其为一个三角,问着N条线段能组成多少三角。 题目分析: 将垂直线段映射到Y轴上,这个问题就转变成了线段树的区间覆盖问题,需要注意的是如果线段的情况如下图所示: | | | | | | | | | 123 1和3之间仍是水平可见的,但是点映射的时候可能会忽视掉,如果“中空”的那一段也有值比如0.5就不会出现这种问题了,所以我们只需要将所有y坐标乘2即可。 接下来的事情就是线段树的区间覆盖了,在线段树结点中维护一个Color域,用于 表示当前结点的线段颜色,如果有多种颜色,则标记为-1,每次插入操作的时候,如果插入的线段完全覆盖了当前区间,那么判断Color域是否为-1,如果不是-1的话,说明当前线段的颜色必定只有一种,直接覆盖后改变Color域,否则继续递归左右子树。并且将Color域信息传递给左右儿子,在递归结束的时候记得将左右子树的Color域进行一次判断,如果两者的Color域相同,那么父亲的Color域就是子树的Color域,这一步很关键,可以将子树收缩,以免下次访问的时候不用递归太深。
在每次线段覆盖之前先进行询问,将有关系的两条线段建立单向边,所有线段覆盖完毕后进行一次O(n^3)的扫描。
/*
lazy思想
染色模型
适合颜色数目较少(64以内)的区间染色问题。
具体操作:
1、对某个连续区间进行染色。
2、询问某个连续区间的颜色情况(种类、数目等等)。
适用题型:
poj 2777 Count Color
hdu 5023 A Corrupt Mayor's Performance Art
结点存储
颜色值的位或colorBit:每个颜色用2的幂来表示,颜色值表示分别为1、2、4、8 ,该区间有哪些颜色就可以用他们的或来表示 ,该区间有哪些颜色就可以用他们的或来表示
延迟标记lazy:该段区间完全被染色成了lazy这种颜色,这里的lazy要么是2的幂,要么是0
接口说明
giveLazyToSon 传递延迟标记给两个子结点(调用子结点的updateByValue,并且lazy重置)
updateByValue 通过某个颜色值更新当前结点信息(更新colorBit、lazy)
updateFromSon 通过两个子结点更新当前结点信息(更新colorBit)
mergeQuery 询问时用于对分割后的子结点进行合并用,不同情况实现不同
调用说明
建树: 调用静态函数 treeNode::segtree_build(1, 1, n);
插入([x, y], val): 调用静态函数 treeNode::segtree_insert(1, 1, n, x, y, val);
询问([x, y]): 调用静态函数 treeNode::segtree_query(1, 1, n, x, y, ans);
*/ #include <iostream> #include <algorithm> #include <cstdio> #include <vector> using namespace std; #define MAXN 131072 typedef int ValueType; // 返回[l, r]和[x, y]两条线段是否相交
bool is_intersect( int l, int r, int x, int y) { return !(r < x || l > y); } // 返回[x, y]是否完全包含[l, r]
bool is_contain( int l, int r, int x, int y) { return x <= l && r <= y; } struct treeNode { ValueType lazy; ValueType colorBit; int pid; int len; treeNode() { reset(-1, 0); } void reset( int p, int _len) { pid = p; colorBit = 0; lazy = 0; len = _len; } int lson() { return pid << 1; } int rson() { return pid<<1|1; } void updateByValue(ValueType _val); void giveLazyToSon(); void updateFromSon(); // 询问的时候将结点合并后计入答案
void mergeQuery( int p); // 建树
static void segtree_build( int p, int l, int r); // 插入线段[x, y]到[l, r]
static void segtree_insert( int p, int l, int r, int x, int y, ValueType val); // 区间询问[x, y]上的信息
static void segtree_query( int p, int l, int r, int x, int y, int id); }; /* 全局变量
nodes[MAXN*2] 存储所有静态线段树结点(动态开内存太费时间)
totalNodes 存储结点数目
*/treeNode nodes[MAXN*2]; vector < int> adj[MAXN]; int adjHash[MAXN], adjHashCount = 0; void treeNode::updateByValue(ValueType _val) { lazy = _val; colorBit = _val; } void treeNode::giveLazyToSon() { if(lazy) { nodes[ lson() ].updateByValue(lazy); nodes[ rson() ].updateByValue(lazy); lazy = 0; } } void treeNode::updateFromSon() { int lc = nodes[ lson() ].colorBit; int rc = nodes[ rson() ].colorBit; if(lc == -1 || rc == -1) { colorBit = -1; } else { colorBit = (lc == rc) ? lc : -1; } } void treeNode::mergeQuery( int p) { colorBit |= nodes[p].colorBit; } void treeNode::segtree_build( int p, int l, int r) { // 创建线段树结点的时候只需要知道该线段树结点管辖区间的长度,区间端点不用存,可以在递归的时候作为函数传参
nodes[p].reset(p, r-l+1); if (l < r) { int mid = (l + r) >> 1; // 递归创建左右儿子结点
treeNode::segtree_build(p<<1, l, mid); treeNode::segtree_build(p<<1|1, mid+1, r); nodes[p].updateFromSon(); } } void treeNode::segtree_insert( int p, int l, int r, int x, int y, ValueType val) { if( !is_intersect(l, r, x, y) ) { return ; } if( is_contain(l, r, x, y) ) { nodes[p].updateByValue(val); return ; } nodes[p].giveLazyToSon(); int mid = (l + r) >> 1; treeNode::segtree_insert(p<<1, l, mid, x, y, val); treeNode::segtree_insert(p<<1|1, mid+1, r, x, y, val); nodes[p].updateFromSon(); } void treeNode::segtree_query( int p, int l, int r, int x, int y, int id) { if( !is_intersect(l, r, x, y) ) { return ; } if( is_contain(l, r, x, y) ) { int preid = nodes[p].colorBit; if( preid != -1 ) { if( adjHash[ preid ] < adjHashCount ) { adj[ preid ].push_back( id ); adjHash[ preid ] = adjHashCount; } return ; } } nodes[p].giveLazyToSon(); int mid = (l + r) >> 1; treeNode::segtree_query(p<<1, l, mid, x, y, id); treeNode::segtree_query(p<<1|1, mid+1, r, x, y, id); nodes[p].updateFromSon(); } struct line { int y1, y2, x; }L[MAXN]; int cmp(line a, line b) { return a.x < b.x; } int n = 16001, m; int segHash[MAXN], segHashCount; int main() { int i, j, k, t; scanf("%d", &t); while( t-- ) { scanf("%d", &m); for(i = 0; i < m; i++) { scanf("%d %d %d", &L[i].y1, &L[i].y2, &L[i].x); L[i].y1 = L[i].y1 * 2 + 1; L[i].y2 = L[i].y2 * 2 + 1; adj[i+1].clear(); } sort(L, L + m, cmp); treeNode::segtree_build(1, 1, n); for(i = 0; i < m; i++) { adjHashCount ++; int color = i + 1; treeNode::segtree_query(1, 1, n, L[i].y1, L[i].y2, color); treeNode::segtree_insert(1, 1, n, L[i].y1, L[i].y2, color); } int ans = 0; for(i = 1; i <= m; i++) { int u = i; for(j = 0; j < adj[u].size(); j++) { int v = adj[u][j]; segHashCount ++; for(k = 0; k < adj[v].size(); k++) { segHash[ adj[v][k] ] = segHashCount; } for(k = 0; k < adj[u].size(); k++) { if( segHash[ adj[u][k] ] == segHashCount ) { ans ++; } } } } printf("%d\n", ans); } return 0; }
摘要: 题目链接:http://poj.org/problem?id=2760
/**//*题意: 给出N(N <= 500)个不透明矩形和它的高度,矩形上方有一盏灯,可以通过照射投影到地面上,不被矩形投影覆盖的就会照亮,问最后照亮的区域的面积。解法:离散化+线段树思路: 如果我们知道每... 阅读全文
摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2665
/**//*题意: 给出一个长度为N(N <= 100000)的数列,然后是一连串询问,询问数<= 100000,询问的格式是a, b, k,问[a, b]区间中的k小数。解法... 阅读全文
摘要: 题目链接:http://poj.org/problem?id=2761
/**//*题意: 给出一个长度为N(N <= 100000)的数列,然后是一连串询问,询问数<= 50000,询问的格式是a, b, k,问[a, b]区间中的k小数。解法:二分+树状数组 或者 二分+归并... 阅读全文
题目链接:http://acm.fzu.edu.cn/problem.php?pid=1608
  /**//* /**//*

 题意: 题意:
 给定M个区间 (1 <= M <= 500000)和这些区间上的权值,求最终并区间的最 给定M个区间 (1 <= M <= 500000)和这些区间上的权值,求最终并区间的最
 大权值总和(某个区间不能被计算两次)。 大权值总和(某个区间不能被计算两次)。

 解法: 解法:
 线段树 线段树

 思路: 思路:
 因为最后询问只有一次,而多次的插入操作,所以这个问题有个很简单的解 因为最后询问只有一次,而多次的插入操作,所以这个问题有个很简单的解
 决办法,每次更新的时候只更新到区间完全覆盖的情况,这样的复杂度是log(n) 决办法,每次更新的时候只更新到区间完全覆盖的情况,这样的复杂度是log(n)
 的,而最后询问的时候来一次O(nlogn)的操作,一直查询到元区间,每次将当前 的,而最后询问的时候来一次O(nlogn)的操作,一直查询到元区间,每次将当前
 区间的最大值向下传递给两个儿子。统计时只要统计元区间的最值和即可。 区间的最大值向下传递给两个儿子。统计时只要统计元区间的最值和即可。
 */ */

 #include <iostream> #include <iostream>

 using namespace std; using namespace std;

 #define maxn 50010 #define maxn 50010

  struct Tree struct Tree  { {
 int Max; int Max;
 int root, l, r; int root, l, r;

 void CoverBy(int lazy); void CoverBy(int lazy);
  int len() int len()  { {
 return r - l; return r - l;
 } }
 }T[maxn*4]; }T[maxn*4];

 int n, m; int n, m;
  void Build(int root, int l, int r) void Build(int root, int l, int r)  { {
 T[root].root = root; T[root].root = root;
 T[root].l = l; T[root].l = l;
 T[root].r = r; T[root].r = r;
 T[root].Max = 0; T[root].Max = 0;
  if(l + 1 == r || l == r) if(l + 1 == r || l == r)  { {
 return ; return ;
 } }
 int mid = (l + r) >> 1; int mid = (l + r) >> 1;
 Build(root<<1, l, mid); Build(root<<1, l, mid);
 Build(root<<1|1, mid, r); Build(root<<1|1, mid, r);
 } }

  void Tree::CoverBy(int lazy) void Tree::CoverBy(int lazy)  { {
  if(lazy > Max) if(lazy > Max)  { {
 Max = lazy; Max = lazy;
 } }
 } }

  void Insert(int root, int l, int r, int val) void Insert(int root, int l, int r, int val)  { {
  if(l >= T[root].r || r <= T[root].l) if(l >= T[root].r || r <= T[root].l)  { {
 return ; return ;
 } }
  if(l <= T[root].l && T[root].r <= r) if(l <= T[root].l && T[root].r <= r)  { {
 T[root].CoverBy(val); T[root].CoverBy(val);
 return ; return ;
 } }
 Insert(root<<1, l, r, val); Insert(root<<1, l, r, val);
 Insert(root<<1|1, l, r, val); Insert(root<<1|1, l, r, val);
 } }

  int Query(int root, int l, int r) int Query(int root, int l, int r)  { {
  if(l + 1 == r) if(l + 1 == r)  { {
 return T[root].Max; return T[root].Max;
 } }
 T[root<<1].CoverBy(T[root].Max); T[root<<1].CoverBy(T[root].Max);
 T[root<<1|1].CoverBy(T[root].Max); T[root<<1|1].CoverBy(T[root].Max);

 int mid = (l + r) >> 1; int mid = (l + r) >> 1;
 return Query(root<<1, l, mid) + Query(root<<1|1, mid, r); return Query(root<<1, l, mid) + Query(root<<1|1, mid, r);
 } }

  int main() int main()  { {
 int i; int i;
  while(scanf("%d %d", &n, &m) != EOF) while(scanf("%d %d", &n, &m) != EOF)  { {
 Build(1, 0, n); Build(1, 0, n);
  for(i = 0; i < m; i++) for(i = 0; i < m; i++)  { {
 int x, y, z; int x, y, z;
 scanf("%d %d %d", &x, &y, &z); scanf("%d %d %d", &x, &y, &z);
 Insert(1, x, y, z); Insert(1, x, y, z);
 } }
 printf("%d\n", Query(1, 0, n)); printf("%d\n", Query(1, 0, n));
 } }

 return 0; return 0;
 } }
摘要: 题目链接:http://poj.org/problem?id=3225
/**//*题意: 刚开始是一个[0, 65535]的集合,要求通过一些集合操作,最后输出最小的的集合。如果有多个,按结束坐标最小的依次输出,集合操作包括:U T:S = S 并 TI T:S =&n... 阅读全文
摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3397
/**//*题意: 给出一个长度为N(N <= 100000)的数列,然后是五种操作:插入操作:0 a b 将所有[a, b]区间内的数改成01 a b ... 阅读全文
摘要: 题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2301
/**//*题意: 给出N(N <= 2000)组操作,每组操作的形式如下:A B C: 将[A,B]区间内的颜色染成C,C可以是白色或者黑色,序列开始是... 阅读全文
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1698
  /**//* /**//*
 题意: 题意:
 给定一个长度为N(N <= 100000)的数列Si,紧接着Q(1 <= Q <= 100000)条操作 给定一个长度为N(N <= 100000)的数列Si,紧接着Q(1 <= Q <= 100000)条操作
 ,每条操作将[A, B]的区间颜色改成C(权值为C),颜色C最多三种,问最后所有数 ,每条操作将[A, B]的区间颜色改成C(权值为C),颜色C最多三种,问最后所有数
 的权值总和。 的权值总和。

 解法: 解法:
 线段树 线段树

 思路: 思路:
 线段树的区间修改,还是利用lazy思想。线段树结点维护一个Color域和一个 线段树的区间修改,还是利用lazy思想。线段树结点维护一个Color域和一个
 Count域,Color要么是-1表示当前结点有多种颜色,要么是颜色的编号,每次插入 Count域,Color要么是-1表示当前结点有多种颜色,要么是颜色的编号,每次插入
 到完全覆盖时在该结点的Color域上打上一个标记,表示当前颜色,计算当前结点的 到完全覆盖时在该结点的Color域上打上一个标记,表示当前颜色,计算当前结点的
 Count值。如果当前结点的颜色和插入的颜色相同,说明不必再往下插入了。如果没 Count值。如果当前结点的颜色和插入的颜色相同,说明不必再往下插入了。如果没
 有完全覆盖,并且当前结点的颜色单一,那么直接将父亲的值传递给而两个儿子, 有完全覆盖,并且当前结点的颜色单一,那么直接将父亲的值传递给而两个儿子,
 还是同样的道理,之前的儿子如果有lazy标记,肯定是在当前标记之前,所以直接覆 还是同样的道理,之前的儿子如果有lazy标记,肯定是在当前标记之前,所以直接覆
 盖即可。最后通过两个儿子的权值计算当前子树的权值。 盖即可。最后通过两个儿子的权值计算当前子树的权值。
 */ */

 #include <iostream> #include <iostream>

 using namespace std; using namespace std;

 #define maxn 100010 #define maxn 100010
 #define MULTIPLE_COLOR -1 #define MULTIPLE_COLOR -1

  struct Tree struct Tree  { {
 int nColor, nCount; int nColor, nCount;
 int son[2]; int son[2];
 int l, r; int l, r;

  void clear() void clear()  { {
 son[0] = son[1] = -1; son[0] = son[1] = -1;
 nColor = 1; nColor = 1;
 nCount = r - l + 1; nCount = r - l + 1;
 } }

  int len() int len()  { {
 return r - l + 1; return r - l + 1;
 } }

 void TranslateToSon(); void TranslateToSon();
 void UpdateBy(Tree* ls, Tree* rs); void UpdateBy(Tree* ls, Tree* rs);
 }T[ maxn*4 ]; }T[ maxn*4 ];
 int tot; int tot;

  int GetID(int& root, int l, int r) int GetID(int& root, int l, int r)  { {
  if(root == -1) if(root == -1)  { {
 root = tot++; root = tot++;
 T[root].l = l; T[root].l = l;
 T[root].r = r; T[root].r = r;
 T[root].clear(); T[root].clear();
 } }
 return root; return root;
 } }

  void Tree::TranslateToSon() void Tree::TranslateToSon()  { {
  if(nColor != MULTIPLE_COLOR) if(nColor != MULTIPLE_COLOR)  { {
 int mid = (l + r) >> 1; int mid = (l + r) >> 1;
 int i0 = GetID(son[0], l, mid); int i0 = GetID(son[0], l, mid);
 T[i0].nColor = nColor; T[i0].nColor = nColor;
 T[i0].nCount = nColor * T[i0].len(); T[i0].nCount = nColor * T[i0].len();

 int i1 = GetID(son[1], mid+1, r); int i1 = GetID(son[1], mid+1, r);
 T[i1].nColor = nColor; T[i1].nColor = nColor;
 T[i1].nCount = nColor * T[i1].len(); T[i1].nCount = nColor * T[i1].len();

 nColor = MULTIPLE_COLOR; nColor = MULTIPLE_COLOR;
 } }
 } }

  void Tree::UpdateBy(Tree* ls, Tree* rs) void Tree::UpdateBy(Tree* ls, Tree* rs) { {
  if(ls->nColor == rs->nColor) if(ls->nColor == rs->nColor)  { {
 nColor = ls->nColor; nColor = ls->nColor;
  }else }else  { {
 nColor = MULTIPLE_COLOR; nColor = MULTIPLE_COLOR;
 } }
 nCount = ls->nCount + rs->nCount; nCount = ls->nCount + rs->nCount;
 } }


  void Insert(int& root, int nl, int nr, int l, int r, int val) void Insert(int& root, int nl, int nr, int l, int r, int val)  { {
 if(l > nr || r < nl) if(l > nr || r < nl)
 return ; return ;

 GetID(root, l, r); GetID(root, l, r);

 if(T[root].nColor == val) if(T[root].nColor == val)
 return ; return ;

  if(nl <= l && r <= nr) if(nl <= l && r <= nr)  { {
 T[root].nColor = val; T[root].nColor = val;
 T[root].nCount = val * (r - l + 1); T[root].nCount = val * (r - l + 1);
 return ; return ;
 } }
 T[root].TranslateToSon(); T[root].TranslateToSon();

 int mid = (l + r) >> 1; int mid = (l + r) >> 1;
 Insert(T[root].son[0], nl, nr, l, mid, val); Insert(T[root].son[0], nl, nr, l, mid, val);
 Insert(T[root].son[1], nl, nr, mid+1, r, val); Insert(T[root].son[1], nl, nr, mid+1, r, val);

 T[root].UpdateBy(&T[ T[root].son[0] ], &T[ T[root].son[1] ]); T[root].UpdateBy(&T[ T[root].son[0] ], &T[ T[root].son[1] ]);
 } }

 int n, m; int n, m;
  int main() int main()  { {
 int t; int t;
 int Case = 1; int Case = 1;
 scanf("%d", &t); scanf("%d", &t);
  while(t--) while(t--)  { {
 int root = -1; int root = -1;
 tot = 0; tot = 0;
 scanf("%d %d", &n, &m); scanf("%d %d", &n, &m);
 Insert(root, 1, n, 1, n, 1); Insert(root, 1, n, 1, n, 1);
  while(m--) while(m--)  { {
 int x, y, z; int x, y, z;
 scanf("%d %d %d", &x, &y, &z); scanf("%d %d %d", &x, &y, &z);
 Insert(root, x, y, 1, n, z); Insert(root, x, y, 1, n, z);
 } }
 printf("Case %d: The total value of the hook is %d.\n", Case++, T[root].nCount); printf("Case %d: The total value of the hook is %d.\n", Case++, T[root].nCount);
 } }
 return 0; return 0;
 } }
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1754
  /**//* /**//*
 题意: 题意:
 给定一个长度为N(N <= 200000)的数列Si,紧接着Q(1 <= Q <= 5000)条询问 给定一个长度为N(N <= 200000)的数列Si,紧接着Q(1 <= Q <= 5000)条询问
 或者修改,询问是询问区间的最大值,修改是修改某一个位置的值。 或者修改,询问是询问区间的最大值,修改是修改某一个位置的值。

 解法: 解法:
 线段树 或者 RMQ 线段树 或者 RMQ

 思路: 思路:
 最裸的线段树区间最值,维护一颗完全二叉树,每个结点保存两个值,表示该结 最裸的线段树区间最值,维护一颗完全二叉树,每个结点保存两个值,表示该结
 点管理的区间的最大值和最小值,比如1号为根结点,管理区间[1, n],每个结点p有 点管理的区间的最大值和最小值,比如1号为根结点,管理区间[1, n],每个结点p有
 左儿子2*p和右儿子2*p+1,当区间两端点相同时为叶子结点,如果p管理的是[a,b]那 左儿子2*p和右儿子2*p+1,当区间两端点相同时为叶子结点,如果p管理的是[a,b]那
 么2*p则管理区间[a, (a+b)/2],2*p+1管理区间[(a+b)/2+1, b],如此一来就可以通 么2*p则管理区间[a, (a+b)/2],2*p+1管理区间[(a+b)/2+1, b],如此一来就可以通
 过递归,将儿子的信息传递给父亲,直至根节点。 过递归,将儿子的信息传递给父亲,直至根节点。
 */ */


 #include <iostream> #include <iostream>

 using namespace std; using namespace std;

 #define inf -(1<<30) #define inf -(1<<30)
 #define maxn 200010 #define maxn 200010

  struct Tree struct Tree  { {
 int Max; int Max;
 int son[2]; int son[2];
 int l, r; int l, r;

  void clear() void clear()  { {
 son[0] = son[1] = -1; son[0] = son[1] = -1;
 Max = inf; Max = inf;
 } }
 void UpdateBy(Tree* ls, Tree* rs); void UpdateBy(Tree* ls, Tree* rs);
 }T[ maxn*4 ]; }T[ maxn*4 ];

 int root, tot; int root, tot;
 int val[maxn]; int val[maxn];

  int GetID(int& root) int GetID(int& root)  { {
  if(root == -1) if(root == -1)  { {
 root = tot++; root = tot++;
 T[root].clear(); T[root].clear();
 } }
 return root; return root;
 } }
  int mmax(int a, int b) int mmax(int a, int b)  { {
 return a > b ? a : b; return a > b ? a : b;
 } }

  void Tree::UpdateBy(Tree* ls, Tree* rs) void Tree::UpdateBy(Tree* ls, Tree* rs) { {
 Max = mmax(ls->Max, rs->Max); Max = mmax(ls->Max, rs->Max);
 } }

  void Build(int& root, int l, int r) void Build(int& root, int l, int r)  { {
 GetID(root); GetID(root);
 T[root].l = l; T[root].r = r; T[root].l = l; T[root].r = r;
  if(l == r) if(l == r)  { {
 T[root].Max = val[l]; T[root].Max = val[l];
 return ; return ;
 } }
 int mid = (l + r) >> 1; int mid = (l + r) >> 1;
 Build(T[root].son[0], l, mid); Build(T[root].son[0], l, mid);
 Build(T[root].son[1], mid+1, r); Build(T[root].son[1], mid+1, r);
 T[root].UpdateBy(&T[T[root].son[0]], &T[T[root].son[1]]); T[root].UpdateBy(&T[T[root].son[0]], &T[T[root].son[1]]);
 } }

  void Insert(int root, int pos, int val) void Insert(int root, int pos, int val)  { {
 if(pos > T[root].r || pos < T[root].l) if(pos > T[root].r || pos < T[root].l)
 return ; return ;
  if(pos <= T[root].l && T[root].r <= pos) if(pos <= T[root].l && T[root].r <= pos)  { {
 if(val > T[root].Max) if(val > T[root].Max)
 T[root].Max = val; T[root].Max = val;
 return ; return ;
 } }
 Insert(T[root].son[0], pos, val); Insert(T[root].son[0], pos, val);
 Insert(T[root].son[1], pos, val); Insert(T[root].son[1], pos, val);

 T[root].UpdateBy(&T[T[root].son[0]], &T[T[root].son[1]]); T[root].UpdateBy(&T[T[root].son[0]], &T[T[root].son[1]]);
 } }



  int Query(int root, int l, int r) int Query(int root, int l, int r)  { {
 if(l > T[root].r || r < T[root].l) if(l > T[root].r || r < T[root].l)
 return inf; return inf;
  if(l <= T[root].l && T[root].r <= r) if(l <= T[root].l && T[root].r <= r)  { {
 return T[root].Max; return T[root].Max;
 } }
 return mmax(Query(T[root].son[0], l, r), Query(T[root].son[1], l, r)); return mmax(Query(T[root].son[0], l, r), Query(T[root].son[1], l, r));
 } }

 int n, m; int n, m;
  int main() int main()  { {
 int i; int i;
  while(scanf("%d %d", &n, &m) != EOF) while(scanf("%d %d", &n, &m) != EOF)  { {
  for(i = 1; i <= n; i++) for(i = 1; i <= n; i++)  { {
 scanf("%d", &val[i]); scanf("%d", &val[i]);
 } }
 root = -1; root = -1;
 tot = 0; tot = 0;
 Build(root, 1, n); Build(root, 1, n);

  while(m--) while(m--)  { {
 char str[10]; char str[10];
 int A, B; int A, B;
 scanf("%s %d %d", str, &A, &B); scanf("%s %d %d", str, &A, &B);
  if(!strcmp(str, "U")) if(!strcmp(str, "U"))  { {
 Insert(root, A, B); Insert(root, A, B);
  }else }else  { {
 printf("%d\n", Query(root, A, B)); printf("%d\n", Query(root, A, B));
 } }
 } }

 } }
 return 0; return 0;
 } }
摘要: 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3308
/**//*题意: 给出一个长度为N(N <= 100000)的数列,然后是两种操作:U A B: 将第A个数替换为B (下标从零开始)Q A B: 输... 阅读全文
金装泡泡堂 v1.21
本游戏采用DirectX开发,所以玩之前必须先有DX的运行环境DirectX9.0c。
游戏是仿照盛大网络的《泡泡堂》开发的《单机版泡泡堂》
游戏总共分为3个模式:
一、闯关模式
该模式一共有48关,地图均由作者本人精心制作,为双人游戏(或单人)
控制方法:
1P:WSAD控制上下左右,空格放置泡泡,V使用道具,B切换道具。
2P:方向键控制上下左右,回车放置泡泡,Shift使用道具,Ctrl切换道具。
二、DIY模式
由玩家通过地图编辑器自行编辑,然后练手用。
控制方法:
1P:WSAD控制上下左右,空格放置泡泡,V使用道具,B切换道具。
2P:方向键控制上下左右,回车放置泡泡,Shift使用道具,Ctrl切换道具。
三、挑战模式
难度较大的模式,用于单人练习控制。
方向键控制上下左右,空格放置泡泡,Z使用道具,X切换道具。
游戏试玩链接: http://code.google.com/p/sguzty/downloads/detail?name=%E9%87%91%E8%A3%85%E6%B3%A1%E6%B3%A1%E5%A0%82v1.21.rar&can=2&q=   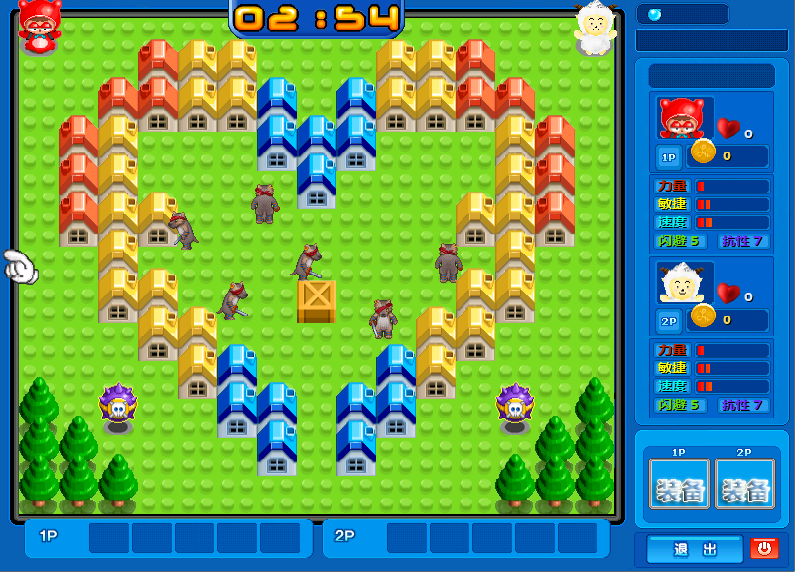    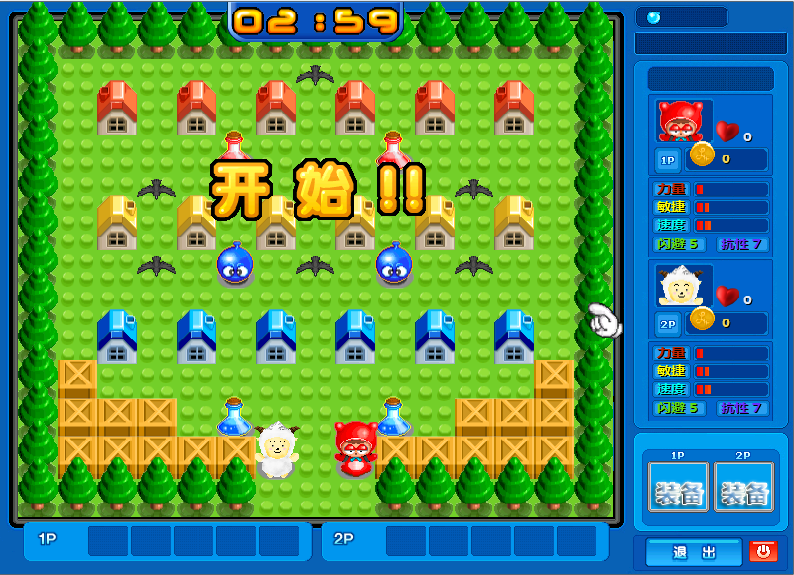 
摘要: 题目链接:http://poj.org/problem?id=2528
/**//*题意: 给定N(N <= 10000)块木板,依次层叠,问最后能从上方俯视的木板的数量。解法:线段树(染色问题)思路: 这题是pku 2777的简化版,木板的数量最多10000种,每个结... 阅读全文
|