http://acm.hdu.edu.cn/showproblem.php?pid=2675
#include<stdio.h>
#include<math.h>
#define e 2.7182818284
double a;
int main()
{
double y,x,start,end,mid;
while(scanf("%lf",&y)==1)
{
a = y*e;
start =1;
end = e;
if((pow(start,a)-pow(a,start))*(pow(end,a)-pow(a,end))<0)
{
while(1)
{
mid = (start+end)/2;
x = pow(mid,a)-pow(a,mid);
if(end-start<0.0000001)
break;
if(x>0)
end = mid;
else
start = mid;
}
if(mid<a)
printf("%.5lf %.5lf\n",mid,a);
else
printf("%.5lf %.5lf\n",a,mid);
}
else
printf("%.5lf\n",a);
}
return 0;
}
求导知道是函数递增的。。
x^ey=(ey)^x
两边ln可以得到
ln(x)/x = ln(ey)/ey
右边是一个常数。
设f(x) = ln(x)/x
求导得到 (1-ln(x))/x^2
在(0,e)是增函数,(e,∞)是减函数
f(0)=0
f(e)=1/e
可得到大致的函数图像如下:
因为y>1 所以ln(ey)/ey的范围在0到1/e之间
然后就可以知道另外一个解的范围是(1,e)
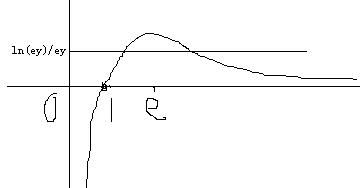
(画的很挫的图)
接下来就是赤裸裸的二分求解。。
又学习了。。
posted on 2009-03-09 21:09
shǎ崽 阅读(364)
评论(0) 编辑 收藏 引用