转自：http://apps.hi.baidu.com/share/detail/17558221
既然是解决寻找两点之间最短路径的的问题。我们自然会想一个描述两点之间最短路径特征的命题。

如果在点A和C之间存在一条最短路径AC，并且在AC上有个点B，那么，沿这条路径产生的路径AB，是点A到点B的最短路径。

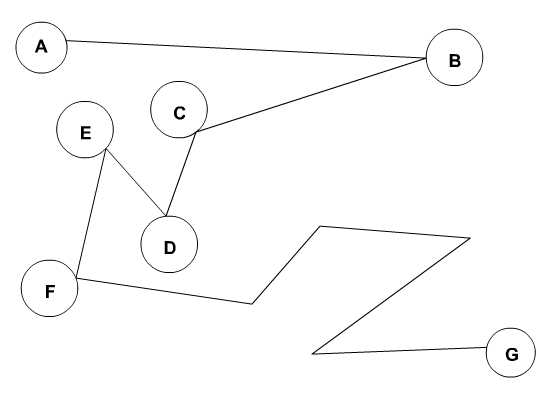
像这张图，如果这条路径是A到G的最短路径，那么AF路径就一定也是A到F的最短路径。

用反证法证明的话，可以这么说。如果存在一条更短的A到F的路径，那么我们完全可以从A走更短的路径到达F，然后再从F到达G，那么产生的路径就比AG要短，这显然和AG是最短路径这个前提矛盾。故AF就一定是最短路径啦。

同理，我们还能推出，AB，AC，AD，甚至BD，BE都是最短路径，这个图中任意两点沿这个路径所产生的路径，都是最短路径。当然，这个最短路径不是唯一的，这只是其中一条。

利用这个数学原理，我们可以在寻路过程中，率先找到起点到某点的一条最短路径，那么之后的所有寻路都基于这个最短路径之上，而不必考虑起点到这个点的其他路径。这样的方法能剔除大量无谓的路径，减少时间和空间的压力。

那么如何率先找到起点到某点的最短路径呢？这里用到数据结构里面的一种广度优先搜索的方法对图进行搜索。

广度优先搜索按照从起点到其他点的路径的长度，从短到长一层一层搜索。当某个点第一次被搜索到，那么所搜索的那个路径就一定是一条最短路径了。这个讲起来有点抽象，下面我们用一张3*3的地图来演示下搜索的过程。

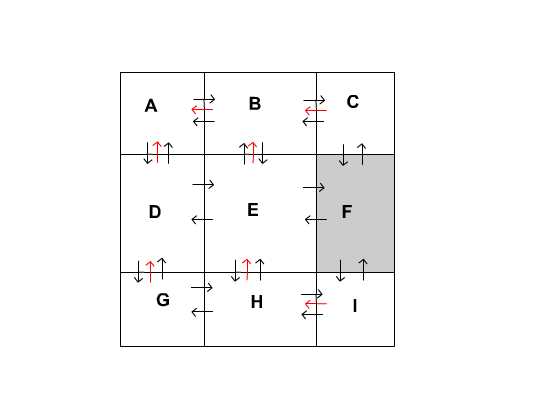
这张地图中，F为障碍物，A是起点，I是终点。每个格子，即一个结点，有三部分和搜索有关的属性。第一个是指向和这个节点相邻的结点的一系列引用（图中黑色箭头表示）。第二个是指向母结点的引用（图中红色箭头表示），在未开始搜索之前，这个属性是空的。第三个就是一个布尔值，表示结点是否是可被搜索的，障碍物默认是不可被搜索的，没有人会产生一个经过障碍物的路径吧，所以这个搜索直接忽略。

将地图连接好之后，我们会产生一个图（此图为数据结构里面的概念），当然，我们也能把这个图看成是一个根节点是起点，元素能重复的无限深度的树。

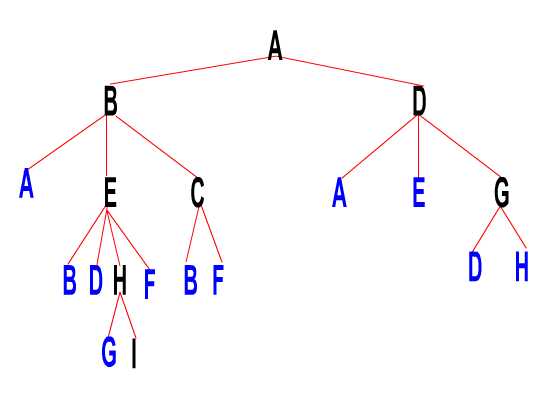
然后我们就开始搜索，首先，从A出发，我们能到B和D，由于B和D是第一次被搜索到，故AB和AD必然是最短路径（这个是不争的事实，他们一步就到了，其他路径皆是绕圈子）。

恩，很好，那么接下来我们就把B和D的指向母结点的引用（上面提到的结点的第二部分属性，也就是地图中画出的红色箭头）指向A，表示从起点到达B和D的最短路径是从A那过来的，这样就把路径储存下来了。

然后，将B和D设为不可搜索，表示B和D的最短路径已经产生了，要是下面要是还搜他们，那么产生的路径一定没这个短，因为搜索的顺序是从短到长的嘛。所以就没有必要对他们搜索了。

最后，将B和D存入第二层的临时数组，第二轮的搜索就要从B和D开始了！

第二轮，首先，从B开始搜索，像刚才从A开始一样。我们发现，B的子节点有三个，其中A被锁定了（蓝色表示，它的子节点由于不参与搜索，就暂时忽略不画），所以直接忽略A。

然后是E和C，发现者两个没有被锁定，那么它们就是第一次出现咯（因为第一次出现后就要被锁定，所以没锁定的就是第一次出现）。恩，把他们像刚才处理B和D一样，设置路径，然后锁定，再存入第三层的临时数组。

B的子节点处理完了，然后是D的子节点。A是锁定的忽略，E刚才在处理B的子节点的时候被锁了，所以也忽略。恩，G第一次出现，把它处理了存入第三层数组，这样，第三层就全部处理完了。下面进入第三轮搜索。

第三轮中，只有H新来的，其他均是老面孔。H存入第四层数组，接下来进入第四轮搜索。

G是老面孔，I是新来的，而且！I就是我们所要的终点。。OK！，搜索就这样结束了！

我们沿着I的指向母结点的引用，I-H-E-B-A，到达起点，这个就是我们要找的路径。

这里，我们不止可以找到起点到终点的最短路径。在搜索过程中，我们已经建立了一个从起点出发，到任何点的最短路径的树。从任何点出发，沿着指向母结点的引用走到起点，都能产生最短路径。