首次发帖，所以有什么不妥之处还请各位多多指教哈~~
http://acm.pku.edu.cn/JudgeOnline/problem?id=1088
滑雪
Description
Michael喜欢滑雪百这并不奇怪， 因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长底滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上，这是最长的一条。
Input
输入的第一行表示区域的行数R和列数C(1 <= R,C <= 100)。下面是R行，每行有C个整数，代表高度h，0<=h<=10000。
Output
输出最长区域的长度。
Sample Input
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
Sample Output
25
Source
SHTSC 2002
2.题目分析：
这是一道比较典型的DP的题，至少，十有八九的人看到这道题就知道这是用动态规划（其实就是一道变相的最长下降子序列），要想写出状态转移方程也不难，唯一的难点可能在于这个是二维的。所以排序和生成状态时就应该换种方法。
首先，贪心肯定不行，例如
|
1
|
24
|
9
|
8
|
3
|
|
24
|
24
|
10
|
7
|
4
|
|
20
|
19
|
12
|
6
|
5
|
|
17
|
18
|
13
|
2
|
2
|
|
16
|
15
|
14
|
2
|
25
|
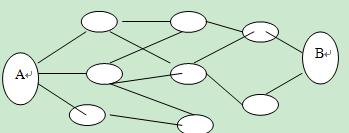
可以从中看出，从最高的贪和从最低的开始贪都是不行的，由数学归纳法可以证明从次高点或次低点开始贪心也不行，依次类推。从图的角度理解，该题目中，每个非边界点可以四向走、边界非顶点点可以三向、顶点可以二向，所以此问题可以等效于从A到B的最短路径的问题，这是不能贪心的。
那么为什么可以动规呢？首先，我们假设每个点与其他点都不连通，那么每个点的最长路径为1。当我们从（相对）最低点（初始状态S0）开始循环时，每一个与它相邻的点与它之间的决策P1都可以初始状态S0来定，在此决策之后，得到相邻点新的状态。可以证明的是，当相对低点的状态都确定之后，所有高点可以滑的长度（状态Sr，r<=sum_of_points）都可以由邻接的低点的状态决定（通过决策）。在其中找最长即可。所以可以用动规。
确定动规之后，先说最重要的：状态转移方程。
Dp[r,c,x]表示：
循环走到第x个高度的时候，各个点的最长滑坡路径状态。
其中所有dp[r,c,0]=0；
Dp[adja_r,adja_c,x]=dp[adja_r,adja_c,x-1], h[adja_r,adja_c,x]<=h[r,c,x-1]
Dp[adja_r,adja_c,x]=max( dp[adja_r,adja_c,x-1], dp[r,c,x-1]+1), h[adja_r,adja_c]>h[r,c]
注意每个点有四个adjacent points。
由此，我们可以写出dp()过程的伪代码：
From 高度小的点 to 高度大的点
对于该点的四向相邻点（注意不要越界）
If （该点h<邻点h）
If （该点dp[][]+1 > 邻点dp[][]）
{邻点 dp[][] = 该点 dp[][]+1;
Longest = max(邻点dp[][], longest);
}
最后输出longest即可。
3.原程序：
1
#include <iostream>
2#include <fstream>
3
4using namespace std;
5
6int n,r,c;
7int h[102][102],len[102][102];
8int longestslope=1;
9
struct Point 
{
10
int row;
11 int column;
12 int val;
13
}p[10002];
14int dir[4][2]={0,-1,-1,0,0,1,1,0};
15
16void dp() {
17
for (int i=1; i<=r*c; i++) {
18 int curr=p[i].row;
19 int curc=p[i].column;
20
21 for (int j=0; j<=3; j++) {
22 int adjar = curr+dir[j][0];
23 int adjac = curc+dir[j][1];
24 //judge if the adjacent point is out of bound;
25 if ( adjar<1 || adjar>r || adjac<1 || adjac>c ) continue;
26
27 if (h[curr][curc] < h[adjar][adjac])
28 if ( len[curr][curc]+1 > len[adjar][adjac] ) {
29 len[adjar][adjac] = len[curr][curc]+1;
30 if (len[adjar][adjac] > longestslope)
31 longestslope = len[adjar][adjac];
32
}
33 }
34 }
35
36}
37
38void qsort(int l, int r) {
39 …
40}
41
42int main() {
43 int n;
44 int cnt=0;
45 scanf("%d %d",&r,&c);
46 for (int i=1; i<=r; i++)
47 for (int j=1; j<=c; j++) {
48 scanf("%d",&h[i][j]);
49 p[++cnt].val=h[i][j];
50 p[cnt].row=i;
51 p[cnt].column=j;
52 len[i][j]=1;
53 }
54
55 qsort(1,r*c);
56 dp();
57 printf("%d\n",longestslope);
58 return 0;
59}
60