**机器中float的二进制舍入问题**
在计算机中,对于精度取舍的问题一直都比较模糊,到底什么时候要舍去,什么时候要输出,下面我就以计算机中的float型为例子,来简单地说一说float的四舍五“入”。
float型在计算机用32位来表示(4个字节),和计算机表示int长度相同,但是表示的机制完全不一样,它由sign,exp,frac部分组成,也就是我们所说的符号位,阶码位,和小数位。
具体的表示方法在这里就不细说了(主要谈论舍入问题)。我们知道的四舍五入就是小于5舍去,大于等于5就进位,那么为什么要这样。举个例子:
1 2 3 4
9 8 7 6 5
比如11,如果在个位运用了四舍五入,那么就会产生一个1的误差(丢失1)得到10.还有19,如果个位数是9的话,相应的产生了1的误差(增加1),四舍五入得到20.所以9个数字中1234恰好和9876对应(后面会说到5),我们期望的是在大量的数据下产生的误差中得到和失去的概率近似为1/2,这就有了四舍五入。但是,我们知道5并没有什么数字和它对应,所以增加的期望值要大于减小的期望值,这是我们不希望看到的。
但是在计算机中所用的表示方法都是二进制的,1,0出现的概率我们可以认为相等。所以,我们就得到了一个新型的四舍五入的方法,小于所对应精度1/2就舍去,大于就进位,等于就有两种情况,一种情况是最低有效位是1,进位。为0,舍去。(向偶取整)
用一道例题来说明:
#include<stdio.h> main() { float a; double b; a = 123456.789e4; b = 123456.789e4; printf(“%f/n%f/n”,a,b); }
运行结果如下:
1234567936.000000
1234567890.000000
由于double的尾数位没有进行舍入操作,因此并没有改变原数,但1234567890>2^23-1要进行舍入操作。
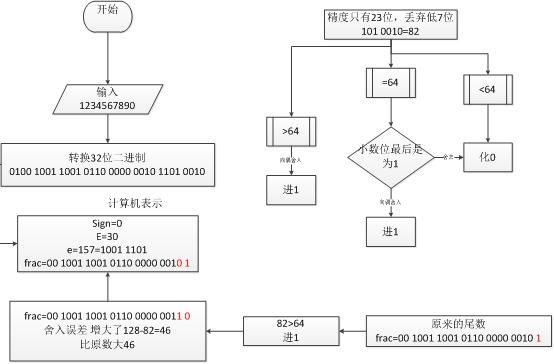
所以就增加了46。