//参考:
http://hi.baidu.com/fandywang_jlu/blog/item/505b40f4c864bddff3d38574.html
http://blog.csdn.net/ldyhot/archive/2008/10/29/3173535.aspx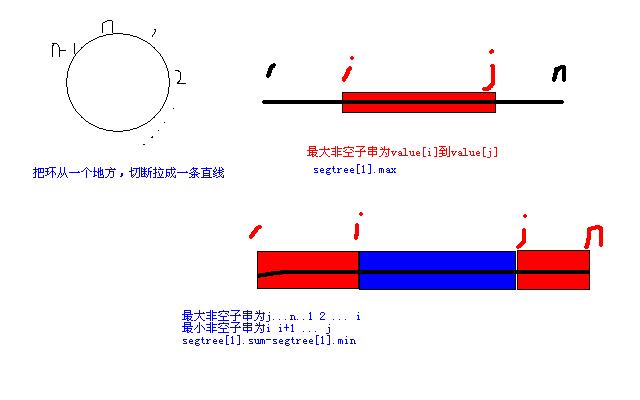
1
 /**//*
/**//*
2 线段树+DP
线段树+DP
3 出题者的简单解题报告:把环从一个地方,切断拉成一条直线,
出题者的简单解题报告:把环从一个地方,切断拉成一条直线,
4 用线段树记录当前区间的非空最大子列和当前区间的非空最小
用线段树记录当前区间的非空最大子列和当前区间的非空最小
5 子列。如果环上的数都是正整数,答案是:环上数的总和-根
子列。如果环上的数都是正整数,答案是:环上数的总和-根
6 结点的非空最小子列;否则,答案是:max{根结点的非空最大
结点的非空最小子列;否则,答案是:max{根结点的非空最大
7 子列, 环上数的总和-根结点的非空最小子列},每次问答的
子列, 环上数的总和-根结点的非空最小子列},每次问答的
8 复杂度是O(logN)。
复杂度是O(logN)。
9 */
*/
10
11 #include<iostream>
#include<iostream>
12 using namespace std;
using namespace std;
13 #define MAXN 100000
#define MAXN 100000
14 #define MAXM 100000
#define MAXM 100000
15 #define MAX 262145
#define MAX 262145
16
17 struct Node
struct Node
18

 {
{
19 int left;
int left;
20 int right;
int right;
21 int sum; //该区间 数的总和
int sum; //该区间 数的总和
22 int max,min; //该区间 最大子列和 与 最小子列和
int max,min; //该区间 最大子列和 与 最小子列和
23 int lmax,rmax; //该区间 从左端点开始的最大子列和 与 到右端点结束的最小子列和
int lmax,rmax; //该区间 从左端点开始的最大子列和 与 到右端点结束的最小子列和
24 int lmin,rmin; //该区间 从左端点开始的最小子列和 与 到右端点结束的最小子列和
int lmin,rmin; //该区间 从左端点开始的最小子列和 与 到右端点结束的最小子列和
25 };
};
26
27 Node segtree[MAX];
Node segtree[MAX];
28 int value[MAXN+1];
int value[MAXN+1];
29 //int vi;
//int vi;
30
31 void update (int v)
void update (int v)
32

 {
{
33 segtree[v].sum=segtree[2*v].sum+segtree[2*v+1].sum;
segtree[v].sum=segtree[2*v].sum+segtree[2*v+1].sum;
34 segtree[v].max=max(max(segtree[2*v].max,segtree[2*v+1].max),segtree[2*v].rmax+segtree[2*v+1].lmax);
segtree[v].max=max(max(segtree[2*v].max,segtree[2*v+1].max),segtree[2*v].rmax+segtree[2*v+1].lmax);
35 segtree[v].min=min(min(segtree[2*v].min,segtree[2*v+1].min),segtree[2*v].rmin+segtree[2*v+1].lmin);
segtree[v].min=min(min(segtree[2*v].min,segtree[2*v+1].min),segtree[2*v].rmin+segtree[2*v+1].lmin);
36 segtree[v].lmax=max(segtree[2*v].lmax, segtree[2*v].sum+segtree[2*v+1].lmax);
segtree[v].lmax=max(segtree[2*v].lmax, segtree[2*v].sum+segtree[2*v+1].lmax);
37 segtree[v].rmax=max(segtree[2*v+1].rmax, segtree[2*v+1].sum+segtree[2*v].rmax);
segtree[v].rmax=max(segtree[2*v+1].rmax, segtree[2*v+1].sum+segtree[2*v].rmax);
38 segtree[v].lmin=min(segtree[2*v].lmin,segtree[2*v].sum+segtree[2*v+1].lmin);
segtree[v].lmin=min(segtree[2*v].lmin,segtree[2*v].sum+segtree[2*v+1].lmin);
39 segtree[v].rmin=min(segtree[2*v+1].rmin,segtree[2*v+1].sum+segtree[2*v].rmin);
segtree[v].rmin=min(segtree[2*v+1].rmin,segtree[2*v+1].sum+segtree[2*v].rmin);
40 }
}
41
42 void build(int v,int l,int r)
void build(int v,int l,int r)
43

 {
{
44 segtree[v].left=l;
segtree[v].left=l;
45 segtree[v].right=r;
segtree[v].right=r;
46
47 if(l == r )
if(l == r )
48

 {
{
49 segtree[v].sum =
segtree[v].sum =
50 segtree[v].max = segtree[v].min =
segtree[v].max = segtree[v].min =
51 segtree[v].lmax = segtree[v].rmax =
segtree[v].lmax = segtree[v].rmax =
52 segtree[v].lmin = segtree[v].rmin =value[l];
segtree[v].lmin = segtree[v].rmin =value[l];
53
54 }else
}else
55

 {
{
56
57 int mid=(segtree[v].left+segtree[v].right)>>1;
int mid=(segtree[v].left+segtree[v].right)>>1;
58 build(2*v,l,mid);
build(2*v,l,mid);
59 build(2*v+1,mid+1,r);
build(2*v+1,mid+1,r);
60 update(v);
update(v);
61 }
}
62
63 }
}
64
65 void insert(int v,int index)
void insert(int v,int index)
66

 {
{
67 if( segtree[v].left == segtree[v].right && segtree[v].left == index)
if( segtree[v].left == segtree[v].right && segtree[v].left == index)
68

 {
{
69 segtree[v].sum =
segtree[v].sum =
70 segtree[v].max = segtree[v].min =
segtree[v].max = segtree[v].min =
71 segtree[v].lmax = segtree[v].rmax =
segtree[v].lmax = segtree[v].rmax =
72 segtree[v].lmin = segtree[v].rmin =value[index];
segtree[v].lmin = segtree[v].rmin =value[index];
73 }else
}else
74

 {
{
75 int mid=(segtree[v].left+segtree[v].right)>>1;
int mid=(segtree[v].left+segtree[v].right)>>1;
76 if(index <= mid) insert(2*v,index);
if(index <= mid) insert(2*v,index);
77 else insert(2*v+1,index);
else insert(2*v+1,index);
78 //if(index <= segtree[2*v].right) insert(2*v,index);
//if(index <= segtree[2*v].right) insert(2*v,index);
79 //else if(index >= segtree[2*v+1].left) insert(2*v+1,index);
//else if(index >= segtree[2*v+1].left) insert(2*v+1,index);
80 update(v);
update(v);
81 }
}
82 }
}
83
84 int main()
int main()
85

 {
{
86 int n,k,i,index;
int n,k,i,index;
87 scanf("%d",&n);
scanf("%d",&n);
88 for(i=1;i<=n;i++)
for(i=1;i<=n;i++)
89 scanf("%d",&value[i]);
scanf("%d",&value[i]);
90
91 build(1,1,n);
build(1,1,n);
92
93 scanf("%d",&k);
scanf("%d",&k);
94 while(k--)
while(k--)
95

 {
{
96 scanf("%d",&index);
scanf("%d",&index);
97 scanf("%d",&value[index]);
scanf("%d",&value[index]);
98 insert(1,index);
insert(1,index);
99 if(segtree[1].sum==segtree[1].max)
if(segtree[1].sum==segtree[1].max)
100 printf("%d\n",segtree[1].sum-segtree[1].min);
printf("%d\n",segtree[1].sum-segtree[1].min);
101 else printf("%d\n",max(segtree[1].max,segtree[1].sum-segtree[1].min));
else printf("%d\n",max(segtree[1].max,segtree[1].sum-segtree[1].min));
102 }
}
103 return 0;
return 0;
104 }
}
105
posted @
2009-04-18 22:41 wyiu 阅读(252) |
评论 (0) |
编辑 收藏
摘要: //离散化+线段树(以下转)感谢它帮助我理解离散化假如不离散化,那线段树的上界是10^7,假如建一个那么大的线段树的话。。。必然MLE。于是要考虑离散化。离散化的目的就是要将线段的长度适当的缩小,但不破坏题意。比如:------ (1,6)------------ (1,12 )像这样这样的两条线段,可以把它们看作:-- (1,2)--- ( 1,3 )这样,缩短了线段的长...
阅读全文
posted @
2009-04-17 19:16 wyiu 阅读(271) |
评论 (0) |
编辑 收藏
摘要: //贡献6个WA//先建树,然后插入,总计,mixcolor表示该段不止一色
1#include<iostream> 2#define MAX 100000 3#define mixcolor -1 4using namespace s...
阅读全文
posted @
2009-04-16 17:01 wyiu 阅读(318) |
评论 (1) |
编辑 收藏
//Sparse Table(ST),动态规划,
<O(N logN), O(1)>
1 void rmq_init()
void rmq_init()
2

 {
{
3 int i,j;
int i,j;
4 for(j=1;j<=n;j++) mx[j][0]=d[j];
for(j=1;j<=n;j++) mx[j][0]=d[j];
5 int m=floor(log((double)n)/log(2.0));
int m=floor(log((double)n)/log(2.0));
6 for(i=1;i<=m;i++)
for(i=1;i<=m;i++)
7 for(j=0;j+(1<<(i-1))<=n;j++)
for(j=0;j+(1<<(i-1))<=n;j++)
8 mx[j][i]=max(mx[j][i-1],mx[j+(1<<(i-1))][i-1]);
mx[j][i]=max(mx[j][i-1],mx[j+(1<<(i-1))][i-1]);
9 }
}
10
11 int rmq(int l,int r)
int rmq(int l,int r)
12

 {
{
13 int m=floor(log((double)(r-l+1))/log(2.0));
int m=floor(log((double)(r-l+1))/log(2.0));
14 int a=max(mx[l][m],mx[r-(1<<m)+1][m]);
int a=max(mx[l][m],mx[r-(1<<m)+1][m]);
15 return a;
return a;
16 }
}
17
18
RMQ介绍:http://baike.baidu.com/view/1536346.htm
摘自某人文章:http://blog.sina.com.cn/s/blog_4d88e9860100cthl.html
posted @
2009-04-14 00:40 wyiu 阅读(171) |
评论 (0) |
编辑 收藏
pku2528-Mayor's posters 区间涂色问题,使用离散化+线段树
pku1151-Atlantis 求矩形并的面积,用线段树+离散化+扫描线
pku1177-picture 求矩形并的周长,用线段树+离散化+扫描线
pku3264-Balanced Lineup RMQ问题,求区间最大最小值的差
pku3368-Frequent values 转化为RMQ问题求解
posted @
2009-04-14 00:31 wyiu 阅读(1997) |
评论 (0) |
编辑 收藏好久没写过算法了,添一个吧,写一个线段树的入门知识,比较大众化。
上次在湖大,其中的一道题数据很强,我试了好多种优化都TLE,相信只能用线段树才能过。回来之后暗暗又学了一次线段树,想想好像是第三次学了,像网络流一样每学一次都有新的体会。
把问题简化一下:
在自然数,且所有的数不大于30000的范围内讨论一个问题:现在已知n条线段,把端点依次输入告诉你,然后有m个询问,每个询问输入一个点,要求这个点在多少条线段上出现过;
最基本的解法当然就是读一个点,就把所有线段比一下,看看在不在线段中;
每次询问都要把n条线段查一次,那么m次询问,就要运算m*n次,复杂度就是O(m*n)
这道题m和n都是30000,那么计算量达到了10^9;而计算机1秒的计算量大约是10^8的数量级,所以这种方法无论怎么优化都是超时
-----
因为n条线段是固定的,所以某种程度上说每次都把n条线段查一遍有大量的重复和浪费;
线段树就是可以解决这类问题的数据结构
举例说明:已知线段[2,5] [4,6] [0,7];求点2,4,7分别出现了多少次
在[0,7]区间上建立一棵满二叉树:(为了和已知线段区别,用【】表示线段树中的线段)
【0,7】
/ \
【0,3】 【4,7】
/ \ / \
【0,1】 【2,3】 【4,5】 【6,7】
/ \ / \ / \ / \
【0,0】 【1,1】【2,2】 【3,3】 【4,4】 【5,5】 【6,6】 【7,7】
每个节点用结构体:
struct line
{
int left,right;//左端点、右端点
int n;//记录这条线段出现了多少次,默认为0
}a[16];
和堆类似,满二叉树的性质决定a[i]的左儿子是a[2*i]、右儿子是a[2*i+1];
然后对于已知的线段依次进行插入操作:
从树根开始调用递归函数insert
1 void insert(int s,int t,int step)//要插入的线段的左端点和右端点、以及当前线段树中的某条线段
void insert(int s,int t,int step)//要插入的线段的左端点和右端点、以及当前线段树中的某条线段
2
3

 {
{
4
5 if (s==a[step].left && t==a[step].right)
if (s==a[step].left && t==a[step].right)
6
7

 {
{
8
9 a[step].n++;//插入的线段匹配则此条线段的记录+1
a[step].n++;//插入的线段匹配则此条线段的记录+1
10
11 return;//插入结束返回
return;//插入结束返回
12
13 }
}
14
15 if (a[step].left==a[step].right) return;//当前线段树的线段没有儿子,插入结束返回
if (a[step].left==a[step].right) return;//当前线段树的线段没有儿子,插入结束返回
16
17 int mid=(a[step].left+a[step].right)/2;
int mid=(a[step].left+a[step].right)/2;
18
19 if (mid>=t) insert(s,t,step*2);//如果中点在t的右边,则应该插入到左儿子
if (mid>=t) insert(s,t,step*2);//如果中点在t的右边,则应该插入到左儿子
20
21 else if (mid<s) insert(s,t,step*2+1);//如果中点在s的左边,则应该插入到右儿子
else if (mid<s) insert(s,t,step*2+1);//如果中点在s的左边,则应该插入到右儿子
22
23 else//否则,中点一定在s和t之间,把待插线段分成两半分别插到左右儿子里面
else//否则,中点一定在s和t之间,把待插线段分成两半分别插到左右儿子里面
24
25

 {
{
26
27 insert(s,mid,step*2);
insert(s,mid,step*2);
28
29 insert(mid+1,t,step*2+1);
insert(mid+1,t,step*2+1);
30
31 }
}
32
33 }
}
34
35
三条已知线段插入过程:
[2,5]
--[2,5]与【0,7】比较,分成两部分:[2,3]插到左儿子【0,3】,[4,5]插到右儿子【4,7】
--[2,3]与【0,3】比较,插到右儿子【2,3】;[4,5]和【4,7】比较,插到左儿子【4,5】
--[2,3]与【2,3】匹配,【2,3】记录+1;[4,5]与【4,5】匹配,【4,5】记录+1
[4,6]
--[4,6]与【0,7】比较,插到右儿子【4,7】
--[4,6]与【4,7】比较,分成两部分,[4,5]插到左儿子【4,5】;[6,6]插到右儿子【6,7】
--[4,5]与【4,5】匹配,【4,5】记录+1;[6,6]与【6,7】比较,插到左儿子【6,6】
--[6,6]与【6,6】匹配,【6,6】记录+1
[0,7]
--[0,7]与【0,7】匹配,【0,7】记录+1
插入过程结束,线段树上的记录如下(红色数字为每条线段的记录n):
【0,7】
1
/ \
【0,3】 【4,7】
0 0
/ \ / \
【0,1】 【2,3】 【4,5】 【6,7】
0 1 2 0
/ \ / \ / \ / \
【0,0】 【1,1】 【2,2】 【3,3】 【4,4】 【5,5】 【6,6】 【7,7】
0 0 0 0 0 0 1 0
询问操作和插入操作类似,也是递归过程,略
2——依次把【0,7】 【0,3】 【2,3】 【2,2】的记录n加起来,结果为2
4——依次把【0,7】 【4,7】 【4,5】 【4,4】的记录n加起来,结果为3
7——依次把【0,7】 【4,7】 【6,7】 【7,7】的记录n加起来,结果为1
不管是插入操作还是查询操作,每次操作的执行次数仅为树的深度——logN
建树有n次插入操作,n*logN,一次查询要logN,m次就是m*logN;总共复杂度O(n+m)*logN,这道题N不超过30000,logN约等于14,所以计算量在10^5~10^6之间,比普通方法快了1000倍;
这道题是线段树最基本的操作,只用到了插入和查找;删除操作和插入类似,扩展功能的还有测度、连续段数等等,在N数据范围很大的时候,依然可以用离散化的方法建树。
湖大的那道题目绕了个小弯子,alpc12有详细的题目和解题报告,有兴趣的话可以看看http://www.cppblog.com/sicheng/archive/2008/01/09/40791.html
线段树的经典题目就是poj1177的picturehttp://acm.pku.edu.cn/JudgeOnline/problem?id=1177
posted @
2009-04-14 00:26 wyiu 阅读(194) |
评论 (0) |
编辑 收藏
(a + b)mod c = (a mod c + b mod c) mod c
(a + b)%c = (a % c + b % c) % c
mod相当于除法,效率低
posted @
2009-04-04 19:52 wyiu 阅读(135) |
评论 (0) |
编辑 收藏 1 #include <limits.h>
#include <limits.h>
2 #include <stdio.h>
#include <stdio.h>
3 #include <stdlib.h>
#include <stdlib.h>
4
5
 /**//* Let INFINITY be an integer value not likely to be
/**//* Let INFINITY be an integer value not likely to be
6 confused with a real weight, even a negative one. */
confused with a real weight, even a negative one. */
7 #define INFINITY ((1 << 14)-1)
#define INFINITY ((1 << 14)-1)
8
9
 typedef struct
typedef struct  {
{
10 int source;
int source;
11 int dest;
int dest;
12 int weight;
int weight;
13 } Edge;
} Edge;
14
15 void BellmanFord(Edge edges[], int edgecount, int nodecount, int source)
void BellmanFord(Edge edges[], int edgecount, int nodecount, int source)
16

 {
{
17 int *distance = (int*) malloc (nodecount * sizeof (*distance)); //int
int *distance = (int*) malloc (nodecount * sizeof (*distance)); //int
18 int i, j;
int i, j;
19
20 for (i=0; i < nodecount; ++i)
for (i=0; i < nodecount; ++i)
21 distance[i] = INFINITY;
distance[i] = INFINITY;
22 distance[source] = 0;
distance[source] = 0;
23
24 for (i=0; i < nodecount; ++i)
for (i=0; i < nodecount; ++i)
25

 {
{
26 int somethingchanged = 0;
int somethingchanged = 0;
27 for (j=0; j < edgecount; ++j)
for (j=0; j < edgecount; ++j)
28

 {
{
29 if (distance[edges[j].source] != INFINITY)
if (distance[edges[j].source] != INFINITY)
30

 {
{
31 int new_distance = distance[edges[j].source] + edges[j].weight;
int new_distance = distance[edges[j].source] + edges[j].weight;
32 if (new_distance < distance[edges[j].dest])
if (new_distance < distance[edges[j].dest])
33

 {
{
34 distance[edges[j].dest] = new_distance;
distance[edges[j].dest] = new_distance;
35 somethingchanged = 1;
somethingchanged = 1;
36 }
}
37 }
}
38 }
}
39
 /**//* if one iteration had no effect, further iterations will have no effect either */
/**//* if one iteration had no effect, further iterations will have no effect either */
40 if (!somethingchanged) break;
if (!somethingchanged) break;
41 }
}
42
43 for (i=0; i < edgecount; ++i)
for (i=0; i < edgecount; ++i)
44

 {
{
45 if (distance[edges[i].dest] > distance[edges[i].source] + edges[i].weight)
if (distance[edges[i].dest] > distance[edges[i].source] + edges[i].weight)
46

 {
{
47 puts("Negative edge weight cycles detected!");
puts("Negative edge weight cycles detected!");
48 free(distance);
free(distance);
49 return;
return;
50 }
}
51 }
}
52
53
 for (i=0; i < nodecount; ++i)
for (i=0; i < nodecount; ++i)  {
{
54 printf("The shortest distance between nodes %d and %d is %d\n",
printf("The shortest distance between nodes %d and %d is %d\n",
55 source, i, distance[i]);
source, i, distance[i]);
56 }
}
57
58 free(distance);
free(distance);
59 return;
return;
60 }
}
61
62 int main(void)
int main(void)
63

 {
{
64
 /**//* This test case should produce the distances 2, 4, 7, -2, and 0. */
/**//* This test case should produce the distances 2, 4, 7, -2, and 0. */
65
 Edge edges[10] =
Edge edges[10] =  {
{ {0,1, 5},
{0,1, 5},  {0,2, 8},
{0,2, 8},  {0,3, -4},
{0,3, -4},  {1,0, -2},
{1,0, -2},
66

 {2,1, -3},
{2,1, -3},  {2,3, 9},
{2,3, 9},  {3,1, 7},
{3,1, 7},  {3,4, 2},
{3,4, 2},
67

 {4,0, 6},
{4,0, 6},  {4,2, 7}};
{4,2, 7}};
68 BellmanFord(edges, 10, 5, 4);
BellmanFord(edges, 10, 5, 4);
69 return 0;
return 0;
70 }
}
71
posted @
2009-04-03 22:08 wyiu 阅读(193) |
评论 (0) |
编辑 收藏Bellman-Ford 算法及其优化
Bellman-Ford算法与另一个非常著名的Dijkstra算法一样,用于求解单源点最短路径问题。Bellman-ford算法除了可求解边权均非负的问题外,还可以解决存在负权边的问题(意义是什么,好好思考),而Dijkstra算法只能处理边权非负的问题,因此 Bellman-Ford算法的适用面要广泛一些。但是,原始的Bellman-Ford算法时间复杂度为 O(VE),比Dijkstra算法的时间复杂度高,所以常常被众多的大学算法教科书所忽略,就连经典的《算法导论》也只介绍了基本的Bellman-Ford算法,在国内常见的基本信息学奥赛教材中也均未提及,因此该算法的知名度与被掌握度都不如Dijkstra算法。事实上,有多种形式的Bellman-Ford算法的优化实现。这些优化实现在时间效率上得到相当提升,例如近一两年被热捧的SPFA(Shortest-Path Faster Algoithm 更快的最短路径算法)算法的时间效率甚至由于Dijkstra算法,因此成为信息学奥赛选手经常讨论的话题。然而,限于资料匮乏,有关Bellman-Ford算法的诸多问题常常困扰奥赛选手。如:该算法值得掌握么?怎样用编程语言具体实现?有哪些优化?与SPFA算法有关系么?本文试图对Bellman-Ford算法做一个比较全面的介绍。给出几种实现程序,从理论和实测两方面分析他们的时间复杂度,供大家在备战省选和后续的noi时参考。
Bellman-Ford算法思想
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图 G=(V,E),其源点为s,加权函数 w是 边集 E 的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。
Bellman-Ford算法流程分为三个阶段:
(1) 初始化:将除源点外的所有顶点的最短距离估计值 d[v] ←+∞, d[s] ←0;
(2) 迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)
(3) 检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 d[v]中。
算法描述如下:
Bellman-Ford(G,w,s) :boolean //图G ,边集 函数 w ,s为源点
1 for each vertex v ∈ V(G) do //初始化 1阶段
2 d[v] ←+∞
3 d[s] ←0; //1阶段结束
4 for i=1 to |v|-1 do //2阶段开始,双重循环。
5 for each edge(u,v) ∈E(G) do //边集数组要用到,穷举每条边。
6 If d[v]> d[u]+ w(u,v) then //松弛判断
7 d[v]=d[u]+w(u,v) //松弛操作 2阶段结束
8 for each edge(u,v) ∈E(G) do
9 If d[v]> d[u]+ w(u,v) then
10 Exit false
11 Exit true
下面给出描述性证明:
首先指出,图的任意一条最短路径既不能包含负权回路,也不会包含正权回路,因此它最多包含|v|-1条边。
其次,从源点s可达的所有顶点如果 存在最短路径,则这些最短路径构成一个以s为根的最短路径树。Bellman-Ford算法的迭代松弛操作,实际上就是按顶点距离s的层次,逐层生成这棵最短路径树的过程。
在对每条边进行1遍松弛的时候,生成了从s出发,层次至多为1的那些树枝。也就是说,找到了与s至多有1条边相联的那些顶点的最短路径;对每条边进行第2遍松弛的时候,生成了第2层次的树枝,就是说找到了经过2条边相连的那些顶点的最短路径……。因为最短路径最多只包含|v|-1 条边,所以,只需要循环|v|-1 次。
每实施一次松弛操作,最短路径树上就会有一层顶点达到其最短距离,此后这层顶点的最短距离值就会一直保持不变,不再受后续松弛操作的影响。(但是,每次还要判断松弛,这里浪费了大量的时间,怎么优化?单纯的优化是否可行?)
如果没有负权回路,由于最短路径树的高度最多只能是|v|-1,所以最多经过|v|-1遍松弛操作后,所有从s可达的顶点必将求出最短距离。如果 d[v]仍保持 +∞,则表明从s到v不可达。
如果有负权回路,那么第 |v|-1 遍松弛操作仍然会成功,这时,负权回路上的顶点不会收敛。
例如对于上图,边上方框中的数字代表权值,顶点A,B,C之间存在负权回路。S是源点,顶点中数字表示运行Bellman-Ford算法后各点的最短距离估计值。
此时d[a]的值为1,大于d[c]+w(c,a)的值-2,由此d[a]可以松弛为-2,然后d[b]又可以松弛为-5,d[c]又可以松弛为-7.下一个周期,d[a]又可以更新为更小的值,这个过程永远不会终止。因此,在迭代求解最短路径阶段结束后,可以通过检验边集E的每条边(u,v)是否满足关系式 d[v]> d[u]+ w(u,v) 来判断是否存在负权回路。
posted @
2009-04-03 21:50 wyiu 阅读(248) |
评论 (0) |
编辑 收藏
//直接向后加,不知道怎么证明,悲剧...
1 #include<iostream>
#include<iostream>
2 using namespace std;
using namespace std;
3 int main()
int main()
4

 {
{
5 int n;
int n;
6 int i;
int i;
7 __int64 t=0;
__int64 t=0;
8 scanf("%d",&n);
scanf("%d",&n);
9
 while(n!=0)
while(n!=0) {
{
10 int *h=new int[n];
int *h=new int[n];
11 for(i=0;i<n;i++)
for(i=0;i<n;i++)
12 scanf("%I64d",&h[i]);
scanf("%I64d",&h[i]);
13 for(i=0;i<n;i++)
for(i=0;i<n;i++)
14

 {
{
15 h[i+1]+=h[i];
h[i+1]+=h[i];
16 if(h[i]>=0)
if(h[i]>=0)
17 t+=h[i];
t+=h[i];
18 else t+=-h[i];
else t+=-h[i];
19 }
}
20 printf("%I64d\n",t);
printf("%I64d\n",t);
21 t=0;
t=0;
22 scanf("%d",&n);
scanf("%d",&n);
23 }
}
24 return 0;
return 0;
25 }
}
posted @
2009-04-03 20:13 wyiu 阅读(90) |
评论 (0) |
编辑 收藏