#
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 998 Accepted Submission(s): 336
Problem Description
穿过幽谷意味着离大魔王lemon已经无限接近了！
可谁能想到，yifenfei在斩杀了一些虾兵蟹将后，却再次面临命运大迷宫的考验，这是魔王lemon设下的又一个机关。要知道，不论何人，若在迷宫中被困1小时以上，则必死无疑！
可怜的yifenfei为了去救MM，义无返顾地跳进了迷宫。让我们一起帮帮执着的他吧！
命运大迷宫可以看成是一个两维的方格阵列，如下图所示：
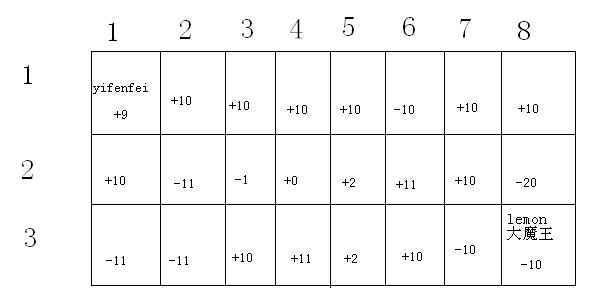
yifenfei一开始在左上角，目的当然是到达右下角的大魔王所在地。迷宫的每一个格子都受到幸运女神眷恋或者痛苦魔王的诅咒，所以每个格子都对应一个值，走到那里便自动得到了对应的值。
现在规定yifenfei只能向右或者向下走，向下一次只能走一格。但是如果向右走，则每次可以走一格或者走到该行的列数是当前所在列数倍数的格子，即：如果当前格子是（x,y），下一步可以是（x+1,y），(x,y+1)或者(x,y*k) 其中k>1。
为了能够最大把握的消灭魔王lemon，yifenfei希望能够在这个命运大迷宫中得到最大的幸运值。
Input
输入数据首先是一个整数C，表示测试数据的组数。
每组测试数据的第一行是两个整数n,m，分别表示行数和列数(1<=n<=20,10<=m<=1000)；
接着是n行数据，每行包含m个整数，表示n行m列的格子对应的幸运值K ( |k|<100 )。
Output
请对应每组测试数据输出一个整数，表示yifenfei可以得到的最大幸运值。
Sample Input
1
3 8
9 10 10 10 10 -10 10 10
10 -11 -1 0 2 11 10 -20
-11 -11 10 11 2 10 -10 -10
Sample Output
Author
yifenfei
Source
Recommend
yifenfei
Statistic |
Submit |
Discuss | Back
DP
1
#include<iostream>
2#include<algorithm>
3using namespace std;
4const int inf=~0U>>1;//取向无穷
5int n,m;
6int a[21][1001];
7int data[21][1001];//记录每一个点的最大幸运值
8
9int max(int a,int b)
10
{
11
return (a>b?a:b);
12
}
13
14void dp()
15{
16 int i,j,u,k;
17 //从一个点可以到达哪些点开始从上到下的遍历
18 for(i=1;i<=n;i++)//寻找每一个点
19 for(j=1;j<=m;j++)
20
{
21 //有两种情况：一个是直接一步向下,还有一个是横向y*k<m
22 for(u=0;u<=1;u++)//u代表的是横向走几步，0还是1
23 {
24 if((u==1)&&(i+u>=1)&&(i+u<=n))//直接向下走一步,而且不超出范围
25 {
26 data[i+u][j]=max(data[i+u][j],data[i][j]+a[i+u][j]);
27
}
28 else//向右前进
29 {
30 if(j+1>=1&&j+1<=m)//在范围以内
31 {
32 data[i][j+1]=max(data[i][j+1],data[i][j]+a[i][j+1]);
33 }
34 for(k=2;k*j<=m;k++) //当u=0的时候k代表的是倍数
35 {
36 if(k*j>=1&&j*k<=m)//不超出范围
37 {
38 data[i][j*k]=max(data[i][j*k],data[i][j]+a[i][j*k]);
39 }
40 }
41 }
42 }
43 }
44 cout<<data[n][m]<<endl;
45
46}
47int main()
48{
49 int c,i,j,k;
50 while(cin>>c)
51 {
52 for(i=1;i<=c;i++)
53 {
54 cin>>n>>m;
55
56 memset(a,0,sizeof(a));//初始化
57 memset(data,0,sizeof(data));
58
59 for(j=1;j<=n;j++)//输入处理
60 for(k=1;k<=m;k++)
61 {
62 cin>>a[j][k];
63 data[j][k]=-inf;//对data数据的再次赋值
64 }
65 data[1][1]=a[1][1];
66
67 dp();
68 }
69 }
70 return 0;
71}
How many ways
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 446 Accepted Submission(s): 304
Problem Description
这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。
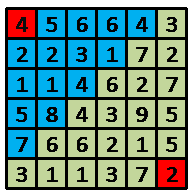
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)
点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。
Input
第一行输入一个整数T,表示数据的组数。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。
Output
对于每一组数据输出方式总数对10000取模的结果.
Sample Input
1
6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2
Sample Output
Author
xhd
Source
2008杭电集训队选拔赛
DP
1
2/**//*
3两种D法,一是对于当前的点,那些点可达;二是当前点可达那些点;
4明显第二种方法高,因为第一种方法有一些没必要的尝试;
5Dp[i][j]+=Dp[ii][jj]; (map[ii][jj]>=两点的曼哈顿距离)
6//用到data[i+k][j+u]=(data[i+k][j+u]+data[i][j])%10000;
7*/
8#include<iostream>
9#include<algorithm>
10using namespace std;
11
12int m,n;
13int a[101][101];
14int data[101][101];
15
16void dp()//动归的函数
17{
18 int i,j,k,u;
19
20 data[1][1]=1;
21
22 for(i=1;i<=n;i++)//每一个点的遍历展开
23 for(j=1;j<=m;j++)
24 {
25 for(k=0;k<=a[i][j];k++)//行向
26 for(u=0;u+k<=a[i][j];u++)//纵向
27 {
28 //保障在范围之内---(k+u)!=0这个条件很重要
29 if((i+k)>=1&&(i+k)<=n&&(j+u)>=1&&(j+u)<=m&&(k+u)!=0)
30 {
31 data[i+k][j+u]=(data[i+k][j+u]+data[i][j])%10000;//中间状态转换方程
32 }
33 }
34 }
35
36 cout<<data[n][m]<<endl;
37
38}
39
40int main()
41{
42 int t,i,j,k;
43 while(cin>>t)
44 {
45 for(k=1;k<=t;k++)
46 {
47 cin>>n>>m;
48 memset(a,0,sizeof(a));//初始化
49 memset(data,0,sizeof(data));
50
51 for(i=1;i<=n;i++)//输入处理
52 for(j=1;j<=m;j++)
53 cin>>a[i][j];
54 dp();
55 }
56 }
57 return 0;
58}
题目来源：http://acm.hdu.edu.cn/showproblem.php?pid=1087
Super Jumping! Jumping! Jumping!
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 6529 Accepted Submission(s): 2569
Problem Description
Nowadays, a kind of chess game called “Super Jumping! Jumping! Jumping!” is very popular in HDU. Maybe you are a good boy, and know little about this game, so I introduce it to you now.
The game can be played by two or more than two players. It consists of a chessboard（棋盘）and some chessmen（棋子）, and all chessmen are marked by a positive integer or “start” or “end”. The player starts from start-point and must jumps into end-point finally. In the course of jumping, the player will visit the chessmen in the path, but everyone must jumps from one chessman to another absolutely bigger (you can assume start-point is a minimum and end-point is a maximum.). And all players cannot go backwards. One jumping can go from a chessman to next, also can go across many chessmen, and even you can straightly get to end-point from start-point. Of course you get zero point in this situation. A player is a winner if and only if he can get a bigger score according to his jumping solution. Note that your score comes from the sum of value on the chessmen in you jumping path.
Your task is to output the maximum value according to the given chessmen list.
Input
Input contains multiple test cases. Each test case is described in a line as follow:
N value_1 value_2 …value_N
It is guarantied that N is not more than 1000 and all value_i are in the range of 32-int.
A test case starting with 0 terminates the input and this test case is not to be processed.
Output
For each case, print the maximum according to rules, and one line one case.
Sample Input
3 1 3 2
4 1 2 3 4
4 3 3 2 1
0
Sample Output
最大递增子段和,状态方程:sum[j]=max{sum[i]}+a[j]; 其中,0<=i<=j,a[i]<a[j]
hdu1087
1#include<iostream>
2#include<algorithm>
3using namespace std;
4
5int n;
6int a[2001];
7__int64 sum[2001],Max;//注意范围
8
9void dp()
10{
11 int i,j;
12 Max=sum[1];
13
14 for(i=1;i<=n;i++)
15 {
16 for(j=1;j<i;j++)
17 {
18 // sum[i]=max(sum[j])+a[i];原理图
19 if((a[j]<a[i])&&(sum[i]<sum[j]+a[i]))
20 {
21 sum[i]=sum[j]+a[i];
22 }
23 if(Max<sum[i])
24 Max=sum[i];
25 }
26 }
27 printf("%I64d\n",Max);
28
29}
30int main()
31{
32 int i;
33 while(cin>>n&&n)
34 {
35 memset(a,0,sizeof(a));//初始化
36 memset(sum,0,sizeof(sum));
37
38 for(i=1;i<=n;i++)
39 {
40 cin>>a[i];
41 sum[i]=a[i];//先每一个sum数组的初始化
42 }
43 dp();//调用DP函数
44 }
45 return 0;
46}
题目来源：
http://acm.hdu.edu.cn/showproblem.php?pid=2084
数塔
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4634 Accepted Submission(s): 2744
Problem Description
在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：
有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？
已经告诉你了，这是个DP的题目，你能AC吗?
Input
输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。
Output
对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。
Sample Input
1
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
Source
数塔
1#include<iostream>
2#include<algorithm>
3using namespace std;
4
5int data[101][101];//保存到节点的路径最大值
6int a[101][101];//用一维数组保存节点
7int n;//层数
8
9int max(int a,int b)
10{
11 return (a>b?a:b);
12}
13
14void dp()//
15{
16 int i,j;
17 data[1][1]=a[1][1];//第一个节点直接是自己
18 for(i=2;i<=n;i++)
19 for(j=1;j<=i;j++)
20 {
21 data[i][j]=max(data[i-1][j-1],data[i-1][j])+a[i][j];//主要DP代码
22 }
23
24}
25int main()
26{
27 int t,i,j,k;
28 while(cin>>t)//几组数据
29 {
30 for(i=1;i<=t;i++)
31 {
32 memset(data,-1,sizeof(data));//初始化
33 memset(a,-1,sizeof(a));
34
35 cin>>n;//n行数据
36 //sum=((1+n)*n)/2;//节点的总个数
37
38 for(j=1;j<=n;j++)//输入节点的数据
39 {
40 for(k=1;k<=j;k++)
41 cin>>a[j][k];//用一维数组
42 }
43 dp();//调用 dp函数
44 int max=data[n][1];
45 for(j=1;j<=n;j++)
46 {
47 if(max<data[n][j])
48 max=data[n][j];
49 }
50 cout<<max<<endl;
51
52 }
53 }
54 return 0;
55}
摘要: H__恶魔猎手会飞了
Time Limit:3000MS Memory Limit:65536KTotal Submit:60 Accepted:15
Description
恶魔猎手成功拿到了古尔丹之颅，吸收了古尔丹之颅的力量后，恶魔猎手全身变的一片漆黑，后背上也长出了一对翅膀，也就是说：他会飞了！！ 兴奋...
阅读全文
Prime Ring Problem
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5409 Accepted Submission(s): 2402
Problem Description
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
Note: the number of first circle should always be 1.
Input
n (0 < n < 20).
Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
Sample Output
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
Source
搜索
1
#include
<
iostream
>
2
using
namespace
std;
3
//
在50以内的素数堆
4
int
prim[
50
]
=
{
0
,
0
,
2
,
3
,
0
,
5
,
0
,
7
,
0
,
0
,
0
,
11
,
0
,
13
,
0
,
0
,
0
,
17
,
0
,
19
,
0
,
0
,
0
,
23
,
0
,
0
,
0
,
0
,
0
,
29
,
0
,
31
,
0
,
0
,
0
,
0
,
0
,
37
,
0
,
0
}
;
//
由于范围是在n (0 < n < 20).所以最大的是19+20=39
5
int
n,t;
6
int
pre_num[
21
];
//
用来保存要输出的数组
7
bool
used[
21
];
//
记录是否这个用到数字
8
9
void
dfs(
int
v,
int
num)
//
num记录的map数组的满足条件的个数,V是当前的一点
10
{
11
int
i;
12
if
(num
==
n)
//
结尾的条件num==n,还要测试是否是环
13
{
14
if
(prim[v
+
1
]
!=
0
)
//
是素数,形成一个素数环
15
{
16
cout
<<
"
1
"
;
17
for
(i
=
2
;i
<
t;i
++
)
18
cout
<<
"
"
<<
pre_num[i];
//
就是先打一个空格再打数字可以避免最后多余的空格
19
cout
<<
endl;
20
}
21
return
;
22
}
23
else
24
{
25
for
(i
=
2
;i
<=
n;i
++
)
26
{
27
if
( used[i]
==
false
&&
prim[i
+
v]
!=
0
)
//
没有记录在内并且满足条件(是素数)
28
{
29
used[i]
=
true
;
//
先标记过
30
31
pre_num[t
++
]
=
i;
//
再添加到数组中
32
33
dfs(i,num
+
1
);
//
递归的两个参数一个代表满足和前面一个数相加为素数的条件，后面一个为num
34
35
used[i]
=
false
;
//
回溯,搜索的关键
36
37
t
--
;
//
回溯的时候数组num要减1
38
}
39
40
}
41
42
}
43
44
}
45
int
main()
46
{
47
int
cas
=
1
;
48
while
(cin
>>
n)
49
{
50
cout
<<
"
Case
"
<<
cas
++<<
"
:
"
<<
endl;
51
memset(used,
0
,
sizeof
(used));
52
53
used[
1
]
=
true
;
//
开始永远是1,Note: the number of first circle should always be 1.
54
t
=
1
;
55
pre_num[t
++
]
=
1
;
//
t是记录数组中暂时的个数
56
57
dfs(
1
,
1
);
//
从1开始
58
cout
<<
endl;
//
最后还有一个大换行
59
}
60
61
return
0
;
62
}
63
Suppose that we have a square city with straight streets. A map of a city is a square board with n rows and n columns, each representing a street or a piece of wall.
A blockhouse is a small castle that has four openings through which to shoot. The four openings are facing North, East, South, and West, respectively. There will be one machine gun shooting through each opening.
Here we assume that a bullet is so powerful that it can run across any distance and destroy a blockhouse on its way. On the other hand, a wall is so strongly built that can stop the bullets.
The goal is to place as many blockhouses in a city as possible so that no two can destroy each other. A configuration of blockhouses is legal provided that no two blockhouses are on the same horizontal row or vertical column in a map unless there is at least one wall separating them. In this problem we will consider small square cities (at most 4x4) that contain walls through which bullets cannot run through.
The following image shows five pictures of the same board. The first picture is the empty board, the second and third pictures show legal configurations, and the fourth and fifth pictures show illegal configurations. For this board, the maximum number of blockhouses in a legal configuration is 5; the second picture shows one way to do it, but there are several other ways.
Your task is to write a program that, given a description of a map, calculates the maximum number of blockhouses that can be placed in the city in a legal configuration.
The input file contains one or more map descriptions, followed by a line containing the number 0 that signals the end of the file. Each map description begins with a line containing a positive integer n that is the size of the city; n will be at most 4. The next n lines each describe one row of the map, with a '.' indicating an open space and an uppercase 'X' indicating a wall. There are no spaces in the input file.
For each test case, output one line containing the maximum number of blockhouses that can be placed in the city in a legal configuration.
Sample input:
4
.X..
....
XX..
....
2
XX
.X
3
.X.
X.X
.X.
3
...
.XX
.XX
4
....
....
....
....
0
Sample output:
5
1
5
2
4
Fire Net
1#include<iostream>
2using namespace std;
3
4char map[4][4];//地图
5int n,maxsum;
6
7bool canput(int row,int col)//判断这点是否可以放置堡垒
8{
9 int i,j;
10 //测试是否可以放碉堡，就是是否有危险
11
12 //先测试col列方向上的
13
14 for(i=row-1;i>=0;--i)
15 {
16 if(map[i][col]=='O')//如果这列上有碉堡
17 return false;
18 if(map[i][col]=='X') break;//如果先遇到的是墙即可以放
19
20 }
21 //从row行方向上的
22 for(j=col-1;j>=0;--j)
23 {
24 if(map[row][j]=='O')
25 return false;
26 if(map[row][j]=='X')
27 break;
28
29 }
30 return true;
31
32
33}
34
35void dfs(int k,int num)//深搜的关键,行向走的，先遍历完一行再遍历一行
36{
37 int x,y;//代表行号和列号
38 if(k==n*n)//终止条件
39 {
40 if(maxsum<num)
41 {
42 maxsum=num;
43 return ;
44 }
45 }
46 else
47 {
48 x=k/n;//行号
49 y=k%n;//列号
50
51 //满足条件可以放堡垒
52 if((map[x][y]=='.')&&(canput(x,y)==true))
53 {
54 //当前点是空白处，并且可以放置碉堡
55 map[x][y]='O';//代替了visit[x][y]==1,来放置堡垒
56 dfs(k+1,num+1);//进入下一个递归,由于满足条件可以放置堡垒，所以num+1
57 map[x][y]='.';//回溯
58
59 }
60 dfs(k+1,num);//有两种用途一种是没有满足条件的递归，还有一种是回溯以后的递归
61 }
62
63}
64int main()
65{
66 int i,j;
67 while( cin>>n && n )
68 {
69 //输入地图的数据
70 for(i=0;i<n;i++)
71 {
72 getchar();
73 for(j=0;j<n;j++)
74 cin>>map[i][j];
75 }
76 //初始化
77 maxsum=0;
78 //开始深搜
79 dfs(0,0);//从第一个结点开始搜索
80 cout<<maxsum<<endl;
81 }
82
83 return 0;
84}
Ignatius and the Princess III
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3088 Accepted Submission(s): 2133
Problem Description
"Well, it seems the first problem is too easy. I will let you know how foolish you are later." feng5166 says.
"The second problem is, given an positive integer N, we define an equation like this:
N=a[1]+a[2]+a[3]+...+a[m];
a[i]>0,1<=m<=N;
My question is how many different equations you can find for a given N.
For example, assume N is 4, we can find:
4 = 4;
4 = 3 + 1;
4 = 2 + 2;
4 = 2 + 1 + 1;
4 = 1 + 1 + 1 + 1;
so the result is 5 when N is 4. Note that "4 = 3 + 1" and "4 = 1 + 3" is the same in this problem. Now, you do it!"
Input
The input contains several test cases. Each test case contains a positive integer N(1<=N<=120) which is mentioned above. The input is terminated by the end of file.
Output
For each test case, you have to output a line contains an integer P which indicate the different equations you have found.
Sample Input
Sample Output
Author
Ignatius.L
1
//
动归是自下而上
2
#include
<
iostream
>
3
using
namespace
std;
4
int
f[
121
][
121
];
5
int
dp(
int
n,
int
k)
//
f[5][1]=f[4][1]+f[3][2]+f[2][3]+f[1][4]+f[0][5]
6
{
7
if
(n
==
0
)
return
1
;
//
所以f[0][5]=1,就是代表的是5=5
8
if
(n
<
k)
return
0
;
//
就是f[1][4]一不能分了=0
9
if
(n
==
k)
return
1
;
//
相当与f[2][2]=1,就是2+2一种
10
if
(f[n][k]
!=-
1
)
return
f[n][k];
//
不用重复计算
11
f[n][k]
=
0
;
//
没有初始化的就先赋值为0;
12
for
(
int
i
=
k;i
<=
n;i
++
)
//
以k为最小开始将n分开
13
f[n][k]
+=
dp(n
-
i,i);
//
f[5][1]=f[4][1]+f[3][2]+f[2][3]+f[1][4]+f[0][5]
14
return
f[n][k];
15
}
16
int
main()
17
{
18
int
n;
19
memset(f,
-
1
,
sizeof
(f));
//
初始化将f[][]数组的值全部赋值为-1
20
while
(cin
>>
n)
21
cout
<<
dp(n,
1
)
<<
endl;
//
假设n=5,则就是f(5,1)
22
return
0
;
23
}
Max Sum
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 38854 Accepted Submission(s): 8400
Problem Description
Given a sequence a[1],a[2],a[3]......a[n], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14.
Input
The first line of the input contains an integer T(1<=T<=20) which means the number of test cases. Then T lines follow, each line starts with a number N(1<=N<=100000), then N integers followed(all the integers are between -1000 and 1000).
Output
For each test case, you should output two lines. The first line is "Case #:", # means the number of the test case. The second line contains three integers, the Max Sum in the sequence, the start position of the sub-sequence, the end position of the sub-sequence. If there are more than one result, output the first one. Output a blank line between two cases.
Sample Input
2
5 6 -1 5 4 -7
7 0 6 -1 1 -6 7 -5
Sample Output
Case 1:
14 1 4
Case 2:
7 1 6
Author
Ignatius.L
1
//
动态规划
2
#include
<
iostream
>
3
using
namespace
std;
4
int
main()
5
{
6
int
T,N,num,start,end;
7
cin
>>
T;
//
输入的是有几行数据
8
for
(
int
i
=
0
;i
<
T;i
++
)
9
{
10
cin
>>
N;
//
输入的是有几列数据
11
int
max
=-
1001
,sum
=
0
,temp
=
1
;
//
一些数据的初始化
12
for
(
int
j
=
0
;j
<
N;j
++
)
13
{
14
cin
>>
num;
//
处理每一个输入的数据
15
sum
+=
num;
16
if
(max
<
sum)
//
如果加上比以前的大则要记录
17
{
18
max
=
sum;
19
start
=
temp;
20
end
=
j
+
1
;
//
指定的是当前的位置
21
}
22
if
(sum
<
0
)
23
{
24
sum
=
0
;
25
temp
=
j
+
2
;
//
将头结点向后移动一位
26
}
27
}
28
cout
<<
"
Case
"
<<
i
+
1
<<
"
:
"
<<
endl
<<
max
<<
"
"
<<
start
<<
"
"
<<
end
<<
endl;
29
if
(i
!=
T
-
1
)
//
最后一行不要换行
30
cout
<<
endl;
31
}
32
return
0
;
33
}