私钥分组加密


上图的证明中,r
(j)两两不同的概率计算是关键,下面给出详细过程

另外两个分布统计的不同意味着计算可分辨(反之则计算不可分辨),亦即r(j)至少两个相同的概率。
Construction 5.3.9一次只能加密与密钥等长的明文,如果要加密更长的明文,怎么办?一个简单直接
的方法是将明文分成多个大小为n的块,对每个块调用上述加密步骤,那么就得到形如下的密文块序列
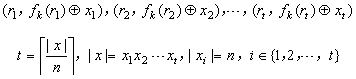
密文块序列从
Proposition 5.3.10的证明中可知是计算不可分辨的,满足
「多组消息安全性
」。但对于解密
需要存储每一块的随机数,因此比较占空间,所以衍生出下面更高效的方案
Construction 5.3.12
私密通用加密

语义安全性分析


抗主动攻击安全性
以上两种构造因满足
「多组消息安全性
」,故满足
CPA与
CCA1,具体的证明可参考Oded Goldreich《密码学基础》的
Proposition 5.4.12、
Proposition 5.4.18。
但不满足
CCA2,因为攻击者拿到挑战密文后,可以修改它再发出解密质疑,得到回答的明文从而异或求解
fk(
ri),最后与挑战密文异或求解挑战明文
对于通用加密构造的CCA2攻击细节如下
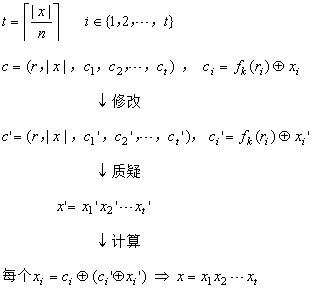
posted on 2024-06-29 17:00
春秋十二月 阅读(617)
评论(0) 编辑 收藏 引用 所属分类:
Algorithm