符号含义与适用前提

二次域的基本结论


x2-dy2=±1
posted @
2024-12-23 11:33 春秋十二月 阅读(281) |
评论 (0) |
编辑 收藏 E 表示满足椭圆曲线Weierstrass方程上的点群
K 代数闭域,用来限制Weierstrass方程的系数与E中的点
E(K) 定义在K上的点群E
E/K 定义在K上的椭圆曲线E
End(E) E上的自同态环
域扩张分析

End(E)模与Z代数

极点首项系数


除子映射及同构

同种映射同态性的解释



Hasse定理之引理证明的补充

挠曲线及其个数

有限域上的椭圆曲线
一种确定型群阶计算法

奇素域上的算法应用


GF域上的群阶计算


Schoof算法正确性根本
一种计算椭圆曲线群的阶的确定型多项式时间算法,确定型是因为算法内部没有随机选择/概率抛币操作,多项式时间是因为域
k的乘法与求逆总次数是O((logq)^6)
(
q为
k的大小,乘法与求逆相对加减运算显著耗时)。具体原理及流程详见参考文献[1]中5.2节。这里给出笔者的一些思考
1. Hasse定理(Frobenius自同态方程式)在扭点群上的限制亦成立,这决定了t模l的一个同余方程成立,且在模l的最小非负剩余系下解是唯一的
2. 孙子定理保证了某取值范围内的一个t模L(L为各素因子l的乘积)的唯一解,即由t模L各个素因子l的同余方程构成的同余方程组的解是唯一的
3. L必须大于t取值上限的2倍。这是为了算法求得的解满足上述2(否则在更小的L内得到的解不唯一,因L与t上限或下限间的某数可以与t模L同余)
4. 素因子l的选择排除2与椭圆曲线特征p。这是因为算法构造所依赖的一个引理之前提条件:为奇素数保证l次除子多项式属于k[X],即引理论断有意义;
不等于p保证检测一个多项式f是否零多项式的充要条件成立,即可以用l次除子多项式去整除f来判断。另l为素数保证了与其它除子多项式(及其幂次)互素
另外发现了算法的一处瑕疵,即第4步预计算除子多项式与Frobenius自同态的复合少了两个值,这导致第5步可能崩溃,当依赖的后续两个复合多项式没被计算时。
这个纠正可通过修改第4步扩大2个值,或第5步通过除子多项式的递推公式按需计算
扭点的阶计算正确性根本

在密码学中的应用
选取原则
1. 排除超奇异椭圆曲线。这是为避免MOV等约化攻击,约化攻击时间复杂度是亚指数
2. 有限域的选择要使E(Fq)的群阶足够大。这是为了缓解Shanks及Pollard ρ攻击
3. E(Fq)存在阶为大素数的子群。这是为了抵抗Pohlig-Hellman攻击
对于第1点,就排除了char(K)=2或3且j(E)=0对应的如下标准形式曲线
Y2+α3Y=X3+α4X+α6(α3≠0) 与 Y2=X3+α4X+α6
一种典型方案
椭圆曲线及有限域的选择使得|E(Fq)|=cm,且char(Fq) ∤ q+1-cm。其中m是一个大素数(通常不低于256位二进制长度,提供中长期安全性),c小于m。
m阶子群的生成元可通过以下方法确定:随机选择E上的一个有理点P,如果Q=cP为零元(即无穷远点),则重复选择,直到其不等于零元。
一旦找到了生成元,那么子群就可以构造出来了。下面分析正确性

参考文献
[1] 椭圆曲线及其在密码学中的应用—导引 Andreas Enge
[2] 算法数论 裴定一、祝跃飞
[3] The Arithmetic of Elliptic Curves Joseph H. Silverman
[4] 标识密码学 程朝辉
[5] 代数学基础与有限域 林东岱
[6] 抽象代数I 赵春来 徐明曜
[7] 代数与数论 李超 周悦
posted @
2024-11-10 21:45 春秋十二月 阅读(278) |
评论 (0) |
编辑 收藏原本算法
摘抄参考文献1中附录的算法流程如下

例子测验


改正后的算法
改正之前,先理清原本算法判别不可约多项式所用的原理。其原理是若f(x)可约,当且仅当存在次数i<=d=[deg(f(x))/2]的不可约因子g(x),而此时gcd(x
q^i-x, f(x))≠1。
根据
参考文献2(详见如下定理),x
q^i-x是所有i次不可约多项式的乘积,因此它必定包含g(x)而与f(x)存在公因子。不可约判别算法的思想应该是遍历次数1到d的所有不可约多项式
(没必要检测大于d的不可约多项式,因为若f(x)可约则其分解因子中必定存在不大于d的不可约多项式),检测输入多项式与它们是否存在公因子。所以这个原理是正确的,只是实现不对,
略作改正如下(类c语言描述)

重新测验


参考文献
[1] 算法数论 裴定一、祝跃飞
[2] 代数学基础与有限域 林东岱
posted @
2024-09-07 23:07 春秋十二月 阅读(302) |
评论 (0) |
编辑 收藏通用算法
先摘抄参考文献[1]中的算法流程如下

正确性分析
下面证明以上算法用到的事实结论,提炼为如下几个引理

 算法构造思想
算法构造思想
用到二次剩余知识,即一个待求平方元ɑ可以且只能表示为两个平方因子的乘积,其中一因子为任意随机选取的非平方因子β的偶数幂,
另一因子为叶子群H的一元素r,H作为陪集划分根群(有限域乘法群)得到β生成的集合即商群G/H的一个代表元系。这样一来,将开方转化为β与r的乘方运算,
迭代的过程就是为求那个具体的代表元β
e中的指数e(注意e必为偶数),从G
s-2到G
0=H,迭代结束后r被唯一确定,r的开方等于r的(t+1)/2次方(因为t是H的阶且为奇数,r
t+1=r)。
观察算法流程,可以发现如果分解q-1后得到s=1,那么就没必要选取非平方元β了(这时令β=1),直接跳到第6步得到结果。仅当s≠1才随机选取β。这样改进后可加快算法运行
例子测验


特殊算法
当q是素数且q≡3(mod 4)时,存在更快的算法及测验如下

posted @
2024-08-30 22:22 春秋十二月 阅读(421) |
评论 (0) |
编辑 收藏基本原理

再来看Terr算法用到的如下定理
定理 (基于
参考文献1改正后的描述)
对每一正整数t,存在唯一确定的一组整数k和j,0<=k<j,使得t=Tj+1-k,其中T0=0,Tn=Tn-1+n-1,n>=1

如果t=0,那么j在区间[0,1),故只能取0,此时k=0与条件k<j矛盾,若允许k=j,则不保证唯一,比如t=1 => j=1, k=0 或 j=2, k=2。
所以参考文献1中原来定理的描述“对每一非负整数t”是错误的。下面列举一些实例验证j与k的唯一解
t=1 => j=1, k=0
t=2 => j=2, k=1
t=3 => j=2, k=0
t=4 => j=3, k=2
t=5 => j=3, k=1
t=6 => j=3, k=0
算法伪代码

例子测验

参考文献
[1] 代数学基础与有限域 林东岱
posted @
2024-08-15 22:35 春秋十二月 阅读(696) |
评论 (0) |
编辑 收藏

上图的证明中,r
(j)两两不同的概率计算是关键,下面给出详细过程

另外两个分布统计的不同意味着计算可分辨(反之则计算不可分辨),亦即r(j)至少两个相同的概率。
Construction 5.3.9一次只能加密与密钥等长的明文,如果要加密更长的明文,怎么办?一个简单直接
的方法是将明文分成多个大小为n的块,对每个块调用上述加密步骤,那么就得到形如下的密文块序列
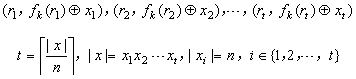
密文块序列从
Proposition 5.3.10的证明中可知是计算不可分辨的,满足
「多组消息安全性
」。但对于解密
需要存储每一块的随机数,因此比较占空间,所以衍生出下面更高效的方案
Construction 5.3.12
私密通用加密

语义安全性分析


抗主动攻击安全性
以上两种构造因满足
「多组消息安全性
」,故满足
CPA与
CCA1,具体的证明可参考Oded Goldreich《密码学基础》的
Proposition 5.4.12、
Proposition 5.4.18。
但不满足
CCA2,因为攻击者拿到挑战密文后,可以修改它再发出解密质疑,得到回答的明文从而异或求解
fk(
ri),最后与挑战密文异或求解挑战明文
对于通用加密构造的CCA2攻击细节如下
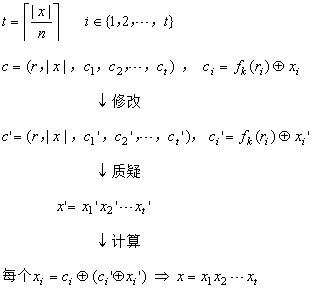
posted @
2024-06-29 17:00 春秋十二月 阅读(607) |
评论 (0) |
编辑 收藏

Berlekamp分解算法

AES有限域

不可约性证明
 非本原性验证
非本原性验证

找出本原元

不可约多项式个数

线性移位寄存器m序列
根据参考文献1知线生移位寄存器产生m序列的充要条件是特征多项式f(x)为本原多项式。而确立有限域上的本原多项式,主要有两种方法:
一种方法是根据
Fq上所有次数为n的本原多项式的乘积正好等于割圆多项式Q
e,其中e=q
n-1,从而所有次数为n的本原多项式可以通过分解Q
e得到。
另一种方法是通过构造本原元再求本原元的极小多项式,先素因子分解q
n-1=p
1p
2...p
k,如果对每一p
i都有ord(
αi)=p
i,那么
α=
α1α2...
αk的阶就是q
n-1,
因此是
Fq上的本原元,则f(x)=(x-
α)(x-
α2)...(x-
αr),r=q
n-1(因为
α是本原元,所以n是使
αq^n=
α成立的最小正整数)。
求解本原多项式
假设线性移位寄存器的级数为4,这里使用上述二种方法求
F16上的本原多项式,过程如下
分解割圆多项式法 
构造极小多项式法 


本原多项式个数

m序列示例

参考文献
[1] 代数学基础与有限域 林东岱
posted @
2024-05-16 13:41 春秋十二月 阅读(891) |
评论 (0) |
编辑 收藏大整数N=pq的素因子p<q<2p,解密指数d<(1/3)N
1/4
【攻击方法】 1)用欧几里得算法计算e/N的各个渐近分数k
i/d
i,i>=1,直至d
i>=(1/3)N
1/4,记录此时的i为m。令i=1
2)计算T=(e*d
i-1)/k
i,若T不为整数则转到4),否则转到3)
3)解方程f(x)=x
2-(N-T+1)x+N=0的根,如果有正整数根且两个根皆小于N,则输出p、q,并返回成功。否则转到4)
4)递增i,若i<m则转回2),否则返回失败
该方法即
Wiener算法用到了关于连分数的一个
定理:若α为任一实数,有理数p/q适合|α-(p/q)|<1/(2q2),则p/q必为α的某一渐近分数。证明详见参考文献[2]。
由定理可知攻击方法是可行的,必能找到使f(x)=0有合理解的某渐近分数。下面证明:攻击迭代次数的上界为
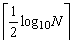 【证明】
【证明】

【例子】N = 9449868410449,e = 6792605526025,d<(1/3)N
1/4≈584,试分解N
 参考文献
参考文献
[1] 公钥密码学的数学基础 王小云、王明强、孟宪萌
[2] 算法数论 裴定一、祝跃飞
posted @
2024-04-04 18:19 春秋十二月 阅读(623) |
评论 (0) |
编辑 收藏
定理1:若G为一个循环群,则G内每个满足ord(
α)=s的元素
α都是拥有s个元素的循环子群的生成元
证明:
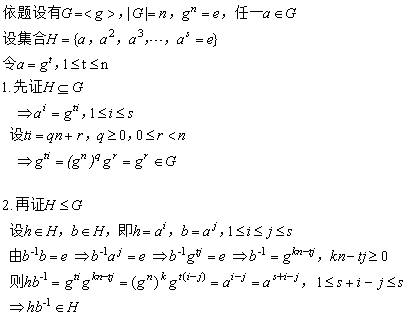 定理2
定理2:若G为一个阶为n的有限循环群,g为对应的生成元,则对整除n的每个整数k,G都存在一个唯一的阶为k的循环子群H。
这个子群是由g
n/k生成的。H是由G内满足条件
αk=1的元素组成的,且G不存在其它子群
证明:

推论:从上述两定理可知有限循环群、子群及生成元的关系如下
 例子
例子:依据上述推论得如下
 生成元判定算法
生成元判定算法
输入:循环群G、某子群的阶k
1)若k=1,则直接输出e。否则转到2)
2)随机从G-{e}中选择一元素x
3)若x
k≠e,则转回2)。否则若k为素数,则跳到5);若k为合数,则转到4)
4)遍历整除k的真因子d,若x
d=e,则转回2)
5)输出x
posted @
2024-03-20 22:49 春秋十二月 阅读(610) |
评论 (0) |
编辑 收藏
X
n ≡ αX
n-1 + c mod m 0<X
0, α, c<m,X
0为种子,n=1、2、3...
定理 如果下列3个条件都满足,则 MLCG达到满周期(即周期d=m)
(1) (c, m)=1,即 c、m互素
(2) 对 m的任一素因子p,有α≡1 mod p
(3) 如果4|m,则 α≡1 mod 4
该定理的证明在
参考文献[2]中证明并用到如下两个引理:
引理5 设p为素数,α∈Z+且pα>2,如果 x=1(mod pα),x≠1(mod pα+1);则xp=1(mod pα+1), xp≠1(mod pα+2)
该引理给出了求一个整数的阶的判别方法,是理解MLCG周期等于m的充要条件之关键。
本文阐述为什么p是使x
p=1(mod p
α+1)成立的最小正整数,以及一般情形m=p
w(w≥1)是使x
m=1(mod p
α+w)成立的最小正整数;为什么前提条件是p
α>2。
◆ 先论证不存在一个整数1≤b<p使得x
b=1(mod p
α+1)成立

◆ 再证不存在一个整数1≤b<m使得x
b=1 (mod p
α+w)成立

◆ 为什么前提条件是pα>2
如果pα=2,x=1(mod 2)且x≠1(mod 22)。令x=1+2q,2 ∤ q。有x2=(1+2q)2=1+4q+4q2,注意到q是奇数,则x2=1(mod22),x2=1(mod23)。故得不到引理的结论
引理6(改写的等价形式) 如果 α=1(mod 4),则(αm - 1)/(α - 1)=0(mod m) ,m=2w,w>1
其实这里当
α=1(mod 2)且
α≠1(mod 4),结论也是成立的。比如取
α=3,m=16,则 (3
16 -1)=81
4 -1=(-15)
4 -1=-15×-7×-7 -1=-15×-15 -1=9×-7 -1=0(mod 32),
即(3
16 -1)/(3-1)=0(mod 16)。但只有当
α=1(mod 4)时,m才是使结论成立的最小正整数。论证如下
 参考文献
参考文献
[1] 现代密码学第4版 杨波
[2] 混合线性同余发生器的周期分析 张广强、张小彩
posted @
2024-03-12 17:30 春秋十二月 阅读(1315) |
评论 (0) |
编辑 收藏