Cake Cutting
Time Limit:1000MS  Memory Limit:65536K
Total Submit:528 Accepted:228

Description

You are given a rectangular cake of integral dimensions w × h. Your goal is to divide this cake into m rectangular pieces of integral dimensions such that the area of the largest piece is minimal. Each cut must be a straight line parallel to one of the sides of the original cake and must divide a piece of cake into two new pieces of positive area. Note that since a cut divides only a single piece, exactly m − 1 cuts are needed.

If w = 4, h = 4, and m = 4, then the following cuts minimize the area of the largest piece:

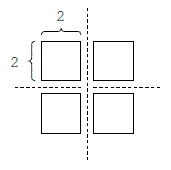
However, if w = 4, h = 4, and m = 3, then the following cuts are optimal:

Input

The input test file will contain multiple test cases, each of which consists of three integers w, h, m separated by a single space, with 1 ≤ w, h, m ≤ 20 and m ≤ wh. The end-of-file is marked by a test case with w = h = m = 0 and should not be processed.

Output

For each test case, write a single line with a positive integer indicating the area of the largest piece.

Sample Input

4 4 4
4 4 3
0 0 0

Sample Output

4
6

Source
Stanford Local 2004

用了记忆化搜索, 900多ms才过掉， rp好啊..

#include  < iostream >
using   namespace  std;

int  f[ 21 ][ 21 ][ 21 ];

int  lookup( int  w,  int  h,  int  k)
{
     if  (f[w][h][k]  >   0 )  return  f[w][h][k];
     if  (k  ==   1 )
     {
        f[w][h][k]  =  w  *  h;
         return  f[w][h][k];
    }
     int  i, j;
     int  max1  =   2000000000 , max2  =   2000000000 ;
     int  t;

     // t = 0;
     for  (i = 1 ; i < w; i ++ )
     {
         for  (j = 1 ; j < k; j ++ )
         {
             if  (i * h  >=  j  &&  (w - i) * h  >=  k - j)
             {
                t  =  lookup(i, h, j)  >  lookup(w - i, h, k - j)  ?  lookup(i, h, j) : lookup(w - i, h, k - j);
                 if  (max1  >  t)
                    max1  =  t;
            }
        }
    }

     // t = 0;
     for  (i = 1 ; i < h; i ++ )
     {
         for  (j = 1 ; j < k; j ++ )
         {
             if  (w * i  >=  j  &&  w * (h - i)  >=  k - j)
             {
                t  =  lookup(w, i, j)  >  lookup(w, h - i, k - j)  ?  lookup(w, i, j) : lookup(w, h - i, k - j);
                 if  (max2  >  t)
                    max2  =  t;
            }
        }
    }

    f[w][h][k]  =  max1  <  max2  ?  max1 : max2;
     return  f[w][h][k];
}

int  g( int  w,  int  h,  int  k)
{
    memset(f,  0 ,  sizeof (f));
     return  lookup(w, h, k);
}

int  main()
{
     int  w, h, m;

     while  (scanf( " %d%d%d " ,  & w,  & h,  & m)  !=  EOF)
     {
         if  (w  ==   0   &&  h  ==   0   &&  m  ==   0 )  break ;
        printf( " %d\n " , g(w, h, m));
    }
     return   0 ;
}