#
2010年1月12日星期二.sgu223
状态压缩动态规划
sgu223:n*n的棋盘上放置k个王的放置方法。
基本方法和pku1185中的递推方法是一样的。
都是先求出一行中的所有合法状态,然后进行按行递推,
在递推的过程中判断两行之间是否有冲突。
#define L(n) (n << 1)
#define R(n) (n >> 1)
#define bin(n) (1 << n)
#define low(n) (n & (-n))
//http://www.cppblog.com/schindlerlee/
const int N = 10;
int n,sum,full;
int s[bin(N)],c[bin(N)],top;
LL f[N+3][bin(N)][N*N];
//行 最后一行状态 已用的王的个数
bool judgeRow(int t)
{
int stat = t,cnt = 0;
int tp = 0,b = 0;
while(t > 0) {
if(b & t) {
return false;
}
b = t & 1,t >>= 1;
if(b == 1) cnt ++;
}
if(sum < cnt)
return false;
s[top] = stat,c[top] = cnt,top++;
return true;
}
bool contradict(int up,int down)
{ return ((up & down) || (L(up) & down) || (R(up) & down)); }
int main()
{
int i,j,k;
scanf("%d%d",&n,&sum);
full = bin(n) - 1;
memset(f,0,sizeof(f));
for(i = 0;i <= full;i++) {
judgeRow(i);
}
f[0][0][0] = 1;
for(i = 1;i <= n;i++) {
for(j = 0;j < top;j++) {
int s1 = s[j],c1 = c[j]; //current
for(k = 0;k < top;k++) {
for(int c2 = 0;c2 <= sum;c2++) {
int s2 = s[k];
if(!f[i-1][s2][c2] ||c1 + c2 > sum) continue;
//状态不可达或者使用王的数量超过k
if(!contradict(s1,s2)) { //状态不冲突
f[i][s1][c1+c2] += f[i-1][s2][c2];
}
}
}
}
}
LL res = 0;
for(i = 0;i <= full;i++) {
res += f[n][i][sum];
}
cout << res << endl;
return 0;
}
2010年1月12日星期二.sgu222
sgu222:n*n棋盘上放置k个车的不同放法
组合数学知识
C(n,k)选k行,然后A(n,k)求n列中k列的全排列
res = C(n,k) * A(n,k) 注意使用long long 型
LL res = 1;
for(i = 2;i <= n;i++) {
res *= i;
}
for(i = 2;i <= n-k;i++) {
res /= i;
}
res *= res;
for(i = 2;i <= k;i++) {
res /= i;
}
cout << res << endl;
2010年1月13日星期三.pku1185
状态压缩动态规划
pku1185:题目是中文的,而且题目很经典,题意不再赘述。
这个题目比pku2411和sgu131两题来说多了一行状态需要储存
因为如果上上行和此行有关
而且此题不再是求完美覆盖的方式,而是求能最大的放置个数。
方法是先求出一行中的所有放置方法。
然后逐行递推,然后在递推的过程中枚举当前行状态,如果和上两行不冲突的话,就
进行放置个数的更新
f[N][60][60] //N行,上一行的状态号,上上行的状态号
具体看代码吧
1
2 /*
3 * SOUR:pku1185
4 * ALGO:State Compression DP
5 * DATE: 2010年 01月 13日 星期三 13:57:49 CST
6 * COMM:4 http://www.cppblog.com/schindlerlee
7 * */
8 #include<iostream>
9 #include<cstdio>
10 #include<cstdlib>
11 #include<cstring>
12 #include<algorithm>
13 using namespace std;
14 typedef long long LL;
15 const int maxint = 0x7fffffff;
16 const long long max64 = 0x7fffffffffffffffll;
17
18 #define bin(i) (1 << (i))
19 #define low(i) ((i) & -(i))
20 #define SL(i) ((i) << 1)
21 #define SR(i) ((i) >> 1)
22
23 void ckmax(int &a, int b)
24 { if (a < b) a = b; }
25
26 const int N = 102;
27 const int M = 10;
28
29 //60是对M==10的一行进行深搜得到的最大状态数量
30 int f[N][60][60], n, m, terrain[N], full;
31 int s[60], top, c[60];
32
33 int legal(int x)
34 {
35 int b = 0, cnt = 0, c;
36 while (x > 0) {
37 cnt++;
38 c = low(x);
39 if (SL(b) & x || SL(SL(b)) & x) {
40 return -1;
41 }
42 x ^= c;
43 b = c;
44 }
45 return cnt;
46 }
47
48 void preprocess()
49 {
50 int i, j, cnt;
51 for (i = 0; i <= full; i++) {
52 if ((cnt = legal(i)) >= 0) {
53 s[top] = i, c[top] = cnt, top++;
54 }
55 }
56 }
57
58 bool contradict(int cur, int s1, int s2)
59 { return (cur & s1) || (cur & s2); }
60
61 int main()
62 {
63 int i, j, k;
64 char str[12];
65 while (scanf("%d%d\n", &n, &m) == 2) {
66 full = bin(m) - 1;
67 preprocess();
68
69 for (i = 1; i <= n; i++) {
70 scanf("%s\n", str);
71 int tmp = 0;
72 for (j = 0; j < m; j++) {
73 tmp <<= 1;
74 if (str[j] == 'H') {
75 tmp |= 1;
76 }
77 }
78 terrain[i] = tmp;
79 }
80
81 for (i = 1; i <= n; i++) {
82 for (j = 0; j < top; j++) { //枚举当前行
83 int cur = s[j], curcnt = c[j];
84 if (cur & terrain[i]) {
85 continue;
86 } //不符合第i行地形要求
87
88 for (int k1 = 0; k1 < top; k1++) { //枚举前两行
89 for (int k2 = 0; k2 < top; k2++) {
90 if (!contradict(cur, s[k1], s[k2])) { //和上两行状态不冲突
91 ckmax(f[i][j][k1], f[i - 1][k1][k2] + curcnt);
92 }
93 }
94 }
95 }
96 }
97
98 int res = 0;
99 for (i = 0; i < top; i++) {
100 for (j = 0; j < top; j++) {
101 ckmax(res, f[n][i][j]);
102 }
103 }
104 printf("%d\n", res);
105 }
106 return 0;
107 }
108
109
2010年1月11日星期一.sgu131 pku2411
状态压缩动态规划。
pku2411:
给一个m*n(m,n<=11)的棋盘,用1*2和2*1的矩形覆盖这个棋盘,问有多少中方法对这个棋盘进行
完全覆盖。
这题有组合数学上的公式,但是只能对棋盘上没有障碍的情况有用,如果遇到有障碍的情况,只能
利用容斥原理进行计算,但是进行容斥原理的会非常复杂。
其实一看到数据范围就应该想到使用位运算的状态压缩动态规划。
主要的程序是
a表示要铺满的这一行的状态,b表示的是铺满上一行的状态a产生的下一行状态。
然后使用状态b继续递推。
1
2 #include<iostream>
3 #include<cstdio>
4 #include<cstdlib>
5 #include<cstring>
6 #include<algorithm>
7 using namespace std;
8 typedef long long LL;
9 const int maxint = 0x7fffffff;
10 const long long max64 = 0x7fffffffffffffffll;
11 #define bin(i) (1 << i) /*1左移i位*/
12 #define emp(a,i) (!(a & bin(i))) /*判断a的i位是否位0*/
13
14 const int N = 1 << 11;
15 LL f[N], g[N];
16 int m, n;
17 int full;
18
19 void dfs(int a, int b, LL k)
20 {
21 if (a == full) { //将a铺满之后形成的所有下一行状态b的铺法都有k种
22 g[b] += k; //产生b的所有状态求和
23 return;
24 }
25 for (int i = 0; i < m; i++) {
26 if (emp(a, i)) {
27 if (i < m - 1 && emp(a, i + 1)) {
28 dfs(a | bin(i) | bin(i + 1), b, k); //横铺
29 }
30 if (emp(b, i)) {
31 dfs(a | bin(i), b | bin(i), k); //竖铺
32 }
33 break;
34 }
35 }
36 }
37
38 int main()
39 {
40 int i, j, k;
41 while(scanf("%d%d", &m, &n) == 2 && m && n) {
42 memset(f,0,sizeof(f));
43 memset(g,0,sizeof(g));
44 full = (1 << m) - 1;
45 f[full] = 1;
46 for (k = 0; k <= n; k++) {
47 for (i = 0; i <= full; i++) {
48 if (f[i]) { //如果此行的状态i可达
49 dfs(i, 0, f[i]);
50 }
51 }
52 for (i = 0; i <= full; i++) {
53 f[i] = g[i];
54 g[i] = 0;
55 }
56 }
57 cout << f[0] << endl;
58 }
59 return 0;
60 }
61
sgu131:pku2411的加强版
多了L型的瓷砖。这个最好是自己考虑一下,其实就是比上边的代码多了几行
const int N = 512;
LL f[N], g[N];
int m, n;
int full;
void dfs(int a, int b, LL k)
{
if (a == full) { //将a铺满之后形成的所有下一行状态b的铺法都有k种
g[b] += k;
return;
}
for (int i = 0; i < m; i++) {
/* 六种铺法,按以下顺序分别是
a:## ## ## # # #
b: # # # ## ##
* */
if (emp(a, i)) {
if (i < m - 1 && emp(a, i + 1)) {
dfs(a | bin(i) | bin(i + 1), b, k);
if (emp(b, i))
dfs(a | bin(i) | bin(i + 1), b | bin(i), k);
if (emp(b, i + 1))
dfs(a | bin(i) | bin(i + 1), b | bin(i + 1), k);
}
if (emp(b, i)) {
dfs(a | bin(i), b | bin(i), k);
if (i > 0 && emp(b, i - 1))
dfs(a | bin(i), b | bin(i) | bin(i - 1), k);
if (i < m - 1 && emp(b, i + 1))
dfs(a | bin(i), b | bin(i) | bin(i + 1), k);
}
break;
}
}
}
2010年1月9日星期六.sgu125
sgu125:搜
题意还是很好理解的,给出一个N*N的矩阵,B[i][j]表示周围有多少个元素比他大,每个元素的取值范围是1-9,最大的复杂度是9^9次方,大约需要5s才能跑出来,肯定需要优化。
由于题目中的限制很多,非常容易想到判断当前B的合法性来判断。
仔细想想,加上一个或者两个剪枝就可以了。
贴个超级丑陋的代码。。。。 这个题的代码写的确实不太好
1 /*
2 * SOUR:sgu125
3 * ALGO:dfs
4 * DATE: 2010年 01月 08日 星期五 22:46:13 CST
5 * COMM:3 http://www.cppblog.com/schindlerlee/
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 using namespace std;
13 typedef long long LL;
14 const int maxint = 0x7fffffff;
15 const long long max64 = 0x7fffffffffffffffll;
16 const int N = 8;
17 int A[N][N];
18 int B[N][N],n;
19 int S[N][N];
20
21 #define PUSH(x,y) (S[x][y]++)
22 #define POP(x,y) (S[x][y]--)
23 #define legal(x,y) (S[x][y] <= B[x][y])
24
25 bool dfs(int x, int y)
26 {
27 if (y == n + 1) {
28 x++, y = 1;
29 }
30
31 if (x == n + 1) {
32 for(int i = 1;i <= n;i++) {
33 for(int j = 1;j <= n;j++) {
34 if(S[i][j] != B[i][j]) return false;
35 }
36 }
37 return true;
38 }
39 if(x == 3 && y == 1) {
40 if(S[1][1] != B[1][1] ||
41 S[1][2] != B[1][2] ||
42 S[1][3] != B[1][3])
43 return false;
44 }
45
46 for (int i = 1; i <= 9; i++) {
47 A[x][y] = i;
48 if (x > 1 && A[x][y] > A[x - 1][y]) {
49 PUSH(x - 1, y);
50 if (y > 1 && A[x][y] > A[x][y - 1]) {
51 PUSH(x, y - 1);
52 if(legal(x-1,y) && legal(x,y-1) && dfs(x,y+1)) return true;
53 else {
54 POP(x-1,y);
55 POP(x,y-1);
56 }
57 } else if (y > 1 && A[x][y] < A[x][y - 1]) {
58 PUSH(x, y);
59 if(legal(x-1,y) && legal(x,y) && dfs(x,y+1)) return true;
60 else {
61 POP(x-1,y);
62 POP(x,y);
63 }
64 } else {
65 if(legal(x-1,y) && dfs(x,y+1)) return true;
66 else {
67 POP(x-1,y);
68 }
69 }
70 } else if (x > 1 && A[x][y] < A[x - 1][y]) {
71 PUSH(x, y);
72 if (y > 1 && A[x][y] > A[x][y - 1]) {
73 PUSH(x, y - 1);
74 if(legal(x,y) && legal(x,y-1) && dfs(x,y+1)) return true;
75 else {
76 POP(x,y);
77 POP(x,y-1);
78 }
79 } else if (y > 1 && A[x][y] < A[x][y - 1]) {
80 PUSH(x, y);
81 if(legal(x,y) && dfs(x,y+1)) return true;
82 else {
83 POP(x,y);
84 POP(x,y);
85 }
86 } else {
87 if(dfs(x,y+1)) return true;
88 else {
89 POP(x,y);
90 }
91 }
92 }else {
93 if (y > 1 && A[x][y] > A[x][y - 1]) {
94 PUSH(x, y - 1);
95 if(dfs(x,y+1)) return true;
96 else {
97 POP(x,y-1);
98 }
99 } else if (y > 1 && A[x][y] < A[x][y - 1]) {
100 PUSH(x, y);
101 if(dfs(x,y+1)) return true;
102 else {
103 POP(x,y);
104 }
105 } else {
106 if(dfs(x,y+1)) return true;
107 else {
108 }
109 }
110 }
111 }
112 return false;
113 }
114
115 int main()
116 {
117 int i, j, k;
118 scanf("%d", &n);
119 for (i = 1; i <= n; i++) {
120 for (j = 1; j <= n; j++) {
121 scanf("%d", &B[i][j]);
122 }
123 }
124
125 if (dfs(1, 1)) {
126 for(int i = 1;i <= n;i++) {
127 for(int j = 1;j <= n;j++) {
128 printf("%d ",A[i][j]);
129 }
130 putchar(10);
131 }
132 }else {
133 puts("NO SOLUTION");
134 }
135 return 0;
136 }
137
2010年1月7日星期四.sgu170
sgu170:
简单题。
题意很简单,就是求两个只有+-组成的字符串,通过互换相邻的两个+-,是否能够由第一个串,变成第二个,给出最短的变换步数。
直觉的想法:广搜
这样显然有问题,字符串长5000,怎么搜复杂度都太高。
猜想:贪心
对于两个字符串a,b,相同的两个区间,如果a[s....t] 和
b[s...t]所含的+-数量一样多,那么由a[s...t] 到 b[s...t]
的最小距离一定是其中减号或者加号的差的绝对值的和
比如:
-+-+-
到
---++
最小步数就是0 + 1 + 2 = 3
本题就直接求两个串的符号差即可
1 http://www.cppblog.com/schindlerlee
2 bool judge()
3 {
4 len1 = strlen(stra);
5 len2 = strlen(strb);
6 if(len1 != len2) return false;
7 int i,res = 0;
8 for(i = 0;i < len1;i++) {
9 if(stra[i] == '-') { out1[top1++] = i; }
10 if(strb[i] == '-') { out2[top2++] = i; }
11 }
12 if(top1 != top2) return false;
13 for(i = 0;i < top1;i++) {
14 res += abs(out1[i] - out2[i]);
15 }
16 printf("%d\n",res);
17 return true;
18 }
19
20
sgu168:猥琐输入输出的应用 + 简单dp
用getchar和putchar进行输入输出,会比scanf和printf快很多很多。
输入
1
2 char t;
3 scanf("%d%d\n", &m, &n);
4 memset(B, 1, sizeof(B));
5 for(i = 1; i <= m; i++) {
6 for(j = 1; j <= n; j++) {
7 minus = 1;
8 tmp = 0;
9 t = getchar();
10 while(t == ' ') t = getchar();
11 if(t == '-') {
12 t = getchar();
13 minus = -1;
14 }
15 while(t != ' ' && t != 10) {
16 tmp = tmp * 10 + t - '0';
17 t = getchar();
18 }
19 A[i][j] = tmp * minus;
20 //scanf("%d", &A[i][j]);
21 }
22 while(t != 10) {t = getchar();}
23 }
输出
1
2 void print(int t)
3 {
4 if(t > -10 && t < 10) {
5 printf("%d",t);
6 return;
7 }
8 if(t < 0) {
9 putchar('-');
10 t = -t;
11 }
12 top = 0;
13 while(t > 0) {
14 out[top++] = t % 10;
15 t /= 10;
16 }
17 for(int i = top - 1;i >= 0;i--) {
18 putchar('0' + out[i]);
19 }
20 }
我sb了好久。。。。没发现还有负数
dp过程
for(int i = n; i >= 1; i--)
for(int j = m; j >= 1; j--)
B[j][i] = min(min(A[j][i], B[j][i + 1]), min(B[j + 1][i], B[j - 1][i + 1]));
977046 03.01.10 15:41 schindlerlee 168 .CPP Accepted 958 ms 8183 kb
2009年12月26日星期六.pku2165
计算几何
算法:将窗口投影到yz平面和xz平面,分别计算
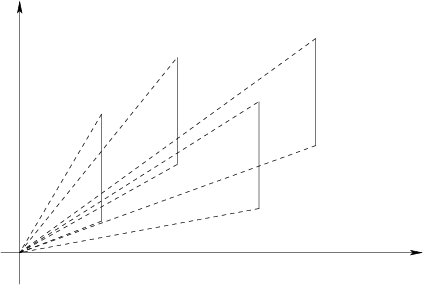
上图是投影到yz平面的情况,可以算出斜率的交区间,如果不存在则无解,然后随便从中选出一个斜率。
然后算出和第一个窗口的Y交点
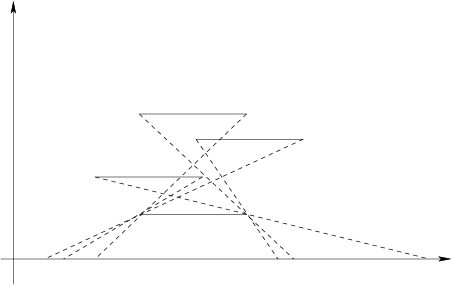
上图是投影到xz平面的情况,需要两两算出直线在x轴上的投影区间,然后随便选一个点作为出始点ansx。
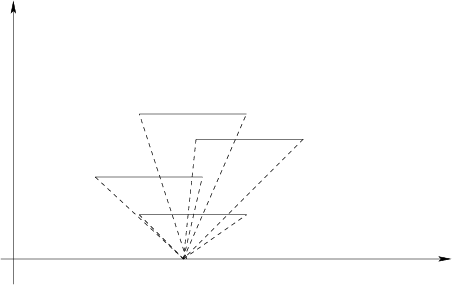
然后由这个点开始,算出斜率的交区间,进而求出和第一条窗的x交点
有了这两个点,就可以利用比例,求出和其他所有窗的交点了
最后,很恶心的是精度,需要特别注意判断无解的情况,一定要用
int dcmp ( double x) { return (x > eps) - (x < -eps);}
我在精度上卡了好几次,最后double eps = 1e-10; 时过的
1 /*
2 * SOUR:pku2165
3 * ALGO:computational geometry
4 * DATE: 2009年 12月 26日 星期六 21:31:06 CST
5 * COMM:4
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 #include<cassert>
13 #include<cmath>
14 using namespace std;
15 typedef long long LL;
16 const int maxint = 0x7fffffff;
17 const long long max64 = 0x7fffffffffffffffll;
18 const int N = 128;
19 int n;
20 double h,ansx,offset;
21 struct W {
22 double x1,y1;
23 double x2,y2,z;
24 }w[N];
25
26 double eps = 1e-10;
27 int dcmp(double x) { return (x > eps) - (x < -eps);}
28
29 const double inf = 1e30;
30
31 void ckmax(double &a,double b) { if(dcmp(a - b) < 0) a = b; }
32 void ckmin(double &a,double b) { if(dcmp(a - b) > 0) a = b; }
33
34 bool CalcY()
35 {
36 int i;
37 double up = inf,down = -inf;
38 for(i = 0;i < n;i++) {
39 ckmax(down,w[i].y1 / w[i].z);
40 ckmin(up,w[i].y2 / w[i].z);
41 }
42 if(dcmp(down - up) > 0) {
43 return false;
44 }
45 double tmp = (up + down)/ 2;
46 h = tmp * w[0].z;
47 //printf("CalcY succeded h = %.6f\n",h);
48 return true;
49 }
50
51 struct P
52 {
53 double x1,x2;
54 }interval[N*N];
55 int top;
56
57 double dist(double a,double b) { return sqrt(a * a + b * b); }
58
59 bool CalcX()
60 {
61 int i ,j;
62 double z,x,len,L;
63 top = 0;
64 for(i = 0;i < n;i++) {
65 for(j = i + 1;j < n;j++) {
66 z = w[j].z - w[i].z;
67 x = w[j].x2 - w[i].x1;
68 len = dist(z,x);
69 L = w[j].z * len / (w[j].z - w[i].z);
70 x = x/len * L;
71 interval[top].x1 = w[j].x2 - x;
72
73 z = w[j].z - w[i].z;
74 x = w[j].x1 - w[i].x2;
75 len = dist(z,x);
76 L = w[j].z * len / (w[j].z - w[i].z);
77 x = x/len * L;
78 interval[top].x2 = w[j].x1 - x;
79
80 top ++;
81 }
82 }
83 double left = -inf,right = inf;
84 for(i = 0;i < top;i++) {
85 //printf("[%d] x1= %.6f,x2 = %.6f\n",i,interval[i].x1,interval[i].x2);
86 ckmax(left,interval[i].x1);
87 ckmin(right,interval[i].x2);
88 }
89 //printf("left = %.6f,right = %.6f\n",left,right);
90 if(dcmp(left - right) > 0)
91 return false;
92 //if(left > right)
93 //return false;
94
95 ansx = (left + right) /2;
96 left = -inf,right = inf;
97 for(i = 0;i < n;i++) {
98 ckmax(left,(w[i].x1 - ansx) / w[i].z);
99 ckmin(right,(w[i].x2 - ansx) / w[i].z);
100 }
101 //assert(left < right);
102 double mid = (left + right)/2;
103 offset = mid * w[0].z;
104 return true;
105 }
106
107
108 int main()
109 {
110 int i,j,k;
111 scanf("%d",&n);
112 for(i = 0;i < n;i++) {
113 scanf("%lf%lf",&w[i].x1,&w[i].y1);
114 scanf("%lf%lf%lf",&w[i].x2,&w[i].y2,&w[i].z);
115 }
116 if(!CalcY()) {
117 printf("UNSOLVABLE\n");
118 return 0;
119 }
120 if(!CalcX()) {
121 printf("UNSOLVABLE\n");
122 return 0;
123 }
124
125 printf("SOLUTION\n");
126 printf("%.6f\n",ansx);
127 for(i = 0;i < n;i++) {
128 double x = w[i].z * offset / w[0].z + ansx;
129 double y = w[i].z * h / w[0].z;
130 double z = w[i].z;
131 printf("%.6f %.6f %.6f\n",x,y,z);
132 }
133 return 0;
134 }
135
136
2009年12月26日星期六.sgu122
半个月了。。。才看出错来。。
构造法很复杂不会,说说搜索的思路:搜索时按每个点临接点的度数从小到大来搜就可以了
此题非常阴险:
1.scanf读入会超时....
2.vector存邻接表一定超时,邻接矩阵又没办法按照度数排序,再开一个矩阵会超内存,第68,69两行只能选一个用,不然会越界
3.每行存的是临接的点,但是没有32~36行会WA @ test 24!!!!!!
4.No Solution是不存在的
1 /*
2 * SOUR:sgu122
3 * ALGO:graph theory
4 * DATE: 2009年 12月 04日 星期五 20:33:43 CST
5 * COMM:5
6 * Ore条件: 对于一个简单图满足任意两个顶点的度数和都大于等于n则必定存在哈密顿回路
7 * * */
8 #include<iostream>
9 #include<cstdio>
10 #include<cstdlib>
11 #include<cstring>
12 #include<algorithm>
13 #include<cassert>
14 #include<vector>
15 using namespace std;
16 const int N = 1001;
17 int cnt[N],deg[N],n,vis[N],out[N],top;
18 int g[N][N];
19 const int M = 6100;
20 char s[M];
21
22 bool cmp(int a,int b) { return deg[a] < deg[b]; }
23 bool dfs(int u,int left)
24 {
25 if(left == 0) {
26 for(int i = 0;i < cnt[u];i++) {
27 if(g[u][i] == 1) {
28 return true;
29 }
30 }
31 //我不知道题目为什么会这么阴险!!
32 for(int i = 0;i < cnt[1];i++) {
33 if(g[1][i] == u) {
34 return true;
35 }
36 }
37 return false;
38 }
39 for(int i = 0;i < cnt[u];i++) {
40 int v = g[u][i];
41 if(!vis[v]) {
42 vis[v] = 1;
43 if(dfs(v,left - 1)) {
44 out[top++] = v;
45 return true;
46 }
47 vis[v] = 0;
48 }
49 }
50 return false;
51 }
52
53 int main()
54 {
55 int i,j,k,tmp,len;
56 scanf("%d\n",&n);
57 for(i = 1;i <= n;i++) {
58 fgets(s,M,stdin);
59 s[(len = strlen(s)) -1] = ' ';
60
61 for(j = 0;j < len;) {
62 k = 0;
63 while(s[j] >= '0') {
64 k = k * 10 + s[j] - '0';
65 j++;
66 }
67 while(s[j] == ' ') {j++;}
68 g[i][cnt[i]++] = k;
69 //g[k][cnt[k]++] = i;
70 deg[k]++;
71 deg[i]++;
72 }
73 }
74 for(i = 1;i <= n;i++) {
75 sort(&g[i][0],&g[i][cnt[i]],cmp);
76 }
77
78 vis[1] = true;
79 dfs(1,n-1);
80 printf("1");
81 for(i = 0;i < top;i++) {
82 printf(" %d",out[i]);
83 }
84 printf(" 1\n");
85
86 return 0;
87 }
88
1 /*
2 * SOUR:sgu139
3 * ALGO:8数码问题的推广
4 * DATE: 2009年 12月 25日 星期五 21:37:54 CST
5 * COMM:4http://www.cppblog.com/schindlerlee
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 using namespace std;
13 typedef long long LL;
14 const int maxint = 0x7fffffff;
15 const long long max64 = 0x7fffffffffffffffll;
16
17 const int N = 16;
18 int num[N];
19 int main()
20 {
21 //最终状态 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0
22 //逆序数15
23 int i,j,offset = 0;
24 int inver = 0;
25 for(i = 0;i < N;i++) {
26 scanf("%d",num + i);
27 if(num[i] == 0) {
28 offset += 3 - (i / 4);
29 offset += 3 - (i % 4);
30 }
31 }
32 for(i = 1;i < N;i++) {
33 for(j = i - 1;j >= 0;j--) {
34 if(num[j] > num[i]) {
35 inver ++;
36 }
37 }
38 }
39 //维度为偶数的这种问题,会改变会改变数列的逆序奇偶性,所以还要判断哈密顿距离的奇偶
40 //维度为奇数的这种问题,则只需要判断逆序的奇偶性
41 //奇偶性相同且offset为偶 或
42 //奇偶性不同且offset为奇 这样的状态都能互相到达
43 if((inver % 2 == 1) == (offset % 2 == 0)) {
44 puts("YES");
45 }else {
46 puts("NO");
47 }
48 return 0;
49 }
50
51
52
2009年12月25日星期五.sgu179
找一个合法的括号序列的下一个合法next_permutation
我打了个表,标*的为正确的排列。
我们发现在()()()()之后的都是非法序列,合法序列只占开始的一小部分。
然后我就用next_permutation水了一下,就过了
WindyWinter还介绍了一个找规律的方法: http://www.briefdream.com/sgu-179/
http://www.cppblog.com/schindlerlee/
/*
00001111 (((()))) *
00010111 ((()())) *
00011011 ((())()) *
00011101 ((()))() *
00011110 ((())))(
00100111 (()(())) *
00101011 (()()()) *
00101101 (()())() *
00101110 (()()))(
00110011 (())(()) *
00110101 (())()() *
00110110 (())())(
00111001 (()))(()
00111010 (()))()(
00111100 (())))((
01000111 ()((())) *
01001011 ()(()()) *
01001101 ()(())() *
01001110 ()(()))(
01010011 ()()(()) *
01010101 ()()()() *
01010110 ()()())(
01011001 ()())(()
01011010 ()())()(
01011100 ()()))((
01100011 ())((())
01100101 ())(()()
01100110 ())(())(
01101001 ())()(()
01101010 ())()()(
01101100 ())())((
01110001 ()))((()
01110010 ()))(()(
01110100 ()))()((
01111000 ())))(((
10000111 )(((()))
10001011 )((()())
10001101 )((())()
10001110 )((()))(
10010011 )(()(())
10010101 )(()()()
10010110 )(()())(
10011001 )(())(()
10011010 )(())()(
10011100 )(()))((
10100011 )()((())
10100101 )()(()()
10100110 )()(())(
10101001 )()()(()
10101010 )()()()(
10101100 )()())((
10110001 )())((()
10110010 )())(()(
10110100 )())()((
10111000 )()))(((
11000011 ))(((())
11000101 ))((()()
11000110 ))((())(
11001001 ))(()(()
11001010 ))(()()(
11001100 ))(())((
11010001 ))()((()
11010010 ))()(()(
11010100 ))()()((
11011000 ))())(((
11100001 )))(((()
11100010 )))((()(
11100100 )))(()((
11101000 )))()(((
11110000 ))))((((
*/
1 /*
2 * SOUR:sgu179
3 * ALGO:math
4 * DATE: 2009年 12月 25日 星期五 16:22:44 CST
5 * COMM:3 http://www.cppblog.com/schindlerlee/
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 using namespace std;
13 typedef long long LL;
14 const int maxint = 0x7fffffff;
15 const long long max64 = 0x7fffffffffffffffll;
16
17 const int N = 10010;
18 char s[N], last[N];
19 int len;
20
21 int judge()
22 //1 right 0 false -1 exceed
23 {
24 int i;
25 for(i = 0;i < len ;i++) {
26 if(last[i] > s[i]) {
27 break;
28 }else if(last[i] < s[i]) {
29 return -1;
30 }
31 }
32 int top = 0;
33 for(int i = 0;i < len;i++) {
34 if(s[i] == '(') {
35 top ++;
36 }else {
37 if(top > 0)
38 top --;
39 else {
40 return 0;
41 }
42 }
43 }
44 return (top == 0);
45 }
46
47 int main()
48 {
49 int i,j,k;
50 scanf("%s",s);
51 len = strlen(s);
52 for(i = 0;i < len;i++) {
53 if(i & 1) {
54 last[i] = ')';
55 }else {
56 last[i] = '(';
57 }
58 }
59
60 next_permutation(s,s + len);
61 while(1) {
62 int r = judge();
63 if(r == 0) {
64 next_permutation(s,s + len);
65 }else if(r == 1) {
66 for(i = 0;i < len;i++) {
67 putchar(s[i]);
68 }
69 putchar(10);
70 break;
71 }else {
72 printf("No solution\n");
73 break;
74 }
75 }
76 return 0;
77 }
78
79
80
2009年12月21日星期一.sgu499
注:此文包括线性筛法,质因子分解,dfs生成一个数的所有因子
sgu499:我想撞墙
http://www.cppblog.com/schindlerlee/
那天arxor看我和angelclover在做,然后也在看题,这个题我还没看,然后arxor大牛就给我说了个想法
把每个数分解素因子,然后dfs出这个数的所有因子。
对每个数进行一次此操作,最后找最大的且被访问了两边以上的因子,
但是这个方法tle在test 20了。怪我当时没细想,被大牛随便一说就觉得这个方法很好。。。。然后。。。杯具了
上代码:tle@20
1 /*
2 * SOUR:sgu Greatest Greatest Common Divisor
3 * ALGO:因子分解
4 * DATE: 2009年 12月 20日 星期日 19:24:49 CST
5 * COMM:3http://www.cppblog.com/schindlerlee/
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 using namespace std;
13 typedef long long LL;
14 const int maxint = 0x7fffffff;
15 const long long max64 = 0x7fffffffffffffffll;
16
17 const int N = 1000010;
18 int vis[N], n, is_prime[N], primes[N], top;
19 int exp[100], num[100], cnt;
20 int can[N];
21 void generate()
22 {
23 int i, j, k;
24 top = 0;
25 fill(is_prime, is_prime + N, 1);
26 for (i = 2; i <= 1000000; i++) {
27 if (is_prime[i]) {
28 primes[top++] = i;
29 }
30 for (j = 0; j < top && i * primes[j] <= 1000000; j++) {
31 is_prime[i * primes[j]] = 0;
32 if (i % primes[j] == 0)
33 break;
34 }
35 }
36 //for(i = 0;i < top;i++) {
37 //printf("%d\n",primes[i]);
38 //}
39 }
40
41 void factor(int x)
42 {
43 //printf("factor %d\n",x);
44 cnt = 0;
45 for (int i = 0; i < top && x > 1; i++) {
46 if (x % primes[i] == 0) {
47 //printf("primes[i] = %d\n",primes[i]);
48 can[i]++;
49 num[cnt] = primes[i];
50 exp[cnt] = 0;
51 while (x % primes[i] == 0) {
52 exp[cnt]++;
53 x /= primes[i];
54 }
55 cnt++;
56 }
57 }
58 }
59
60 void dfs(int x, int level)
61 {
62 if (level == cnt) {
63 //printf("dfs x= %d\n",x);
64 vis[x]++;
65 return;
66 }
67 dfs(x, level + 1);
68 for (int i = 1; i <= exp[level]; i++) {
69 x *= num[level];
70 dfs(x, level + 1);
71 }
72 }
73
74 int main()
75 {
76 int i, j, k;
77 generate();
78 scanf("%d", &n);
79 for (i = 0; i < n; i++) {
80 scanf("%d", &k);
81 factor(k);
82 dfs(1, 0);
83 }
84 for (i = N - 1; i >= 0; i--) {
85 if (vis[i] >= 2) {
86 printf("%d\n", i);
87 break;
88 }
89 }
90 return 0;
91 }
92
然后比赛完google了以下,原来是水题,不予解释了,贴代码
1
2 const int N = 1000010;
3 int vis[N],n,m;
4 void chkmax(int &x,int k) { if(x < k) x = k; }
5 int main()
6 {
7 int i,j,k;
8 scanf("%d",&n);
9 for(i = 0;i < n;i++) {
10 scanf("%d",&k);
11 vis[k] ++;
12 chkmax(m,k);
13 }
14
15 int res = 1;
16 for(i = 2;i <= m;i++) {
17 int tmp = 0;
18 for(j = i;tmp < 2 && j <= m;j += i) {
19 tmp += vis[j];
20 }
21 if(tmp >= 2) res = i;
22 }
23 printf("%d\n",res);
24
25 return 0;
26 }
27
28
结果第二天arxor,说他用那个方法过了。。。。。。。。。
然后我看了他的代码,我发现原来我的因子分解是没有优化的。。。
然后把第45行改成
for (int i = 0; primes[i] * primes[i] <= x && i < top && x > 1; i++) {
过了。。。。。
sgu 144:meeting
纯数学题,算概率
第一个人到达的时间做x轴,第二个人的到达时间做y轴
符合条件的概率是|x-y| <= z
如图所示,正方形和两条直线相交之间的阴影部分面积即是所求。
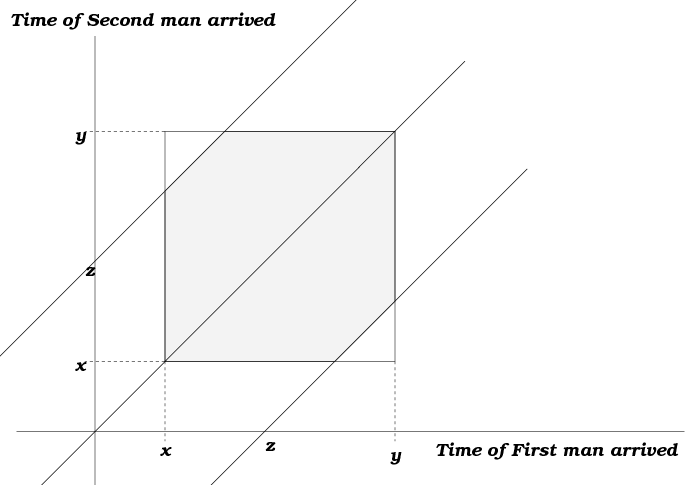
显然的,如果两个人的到达区间不相等,也只要求出矩形和直线相交的面积即可
1 /*
2 * SOUR:sgu144
3 * ALGO:概率
4 * DATE: 2009年 12月 13日 星期日 22:14:36 CST
5 * COMM:3 http://www.cppblog.com/schindlerlee/
6 * 横坐标代表第一个人到达的时间,纵坐标代表第二个人到达的时间
7 * |x-y| <= z
8 * */
9 #include<iostream>
10 #include<cstdio>
11 #include<cstdlib>
12 #include<cstring>
13 #include<algorithm>
14 using namespace std;
15 typedef long long LL;
16 const int maxint = 0x7fffffff;
17 const long long max64 = 0x7fffffffffffffffll;
18
19 double sqr(double x) { return x * x;}
20 int main()
21 {
22 double x,y,z,ans;
23 scanf("%lf%lf%lf",&x,&y,&z);
24 x *= 60,y *= 60;
25 ans = 1 - sqr(y-x-z)/sqr(y - x);
26 printf("%.7f\n",ans);
27 return 0;
28 }
29
30
sgu:169 numbers 纯数学方法
不知道别人是怎么做的,我是纯的打表,找规律。
发现只有11111111....1x的形式才可以,于是就再打个表看看。
11 % = 0
12 % = 0
13 % = 1
14 % = 2
15 % = 0
16 % = 4
17 % = 3
18 % = 2
19 % = 1
111 % = 0
112 % = 0
113 % = 2
114 % = 2
115 % = 0
116 % = 2
117 % = 5
118 % = 6
119 % = 2
1111 % = 0
1112 % = 0
1113 % = 0
1114 % = 2
1115 % = 0
1116 % = 0
1117 % = 4
1118 % = 6
1119 % = 3
11111 % = 0
11112 % = 0
11113 % = 1
11114 % = 2
11115 % = 0
11116 % = 4
11117 % = 1
11118 % = 6
11119 % = 4
111111 % = 0
111112 % = 0
111113 % = 2
111114 % = 2
111115 % = 0
111116 % = 2
111117 % = 6
111118 % = 6
111119 % = 5
1111111 % = 0
1111112 % = 0
1111113 % = 0
1111114 % = 2
1111115 % = 0
1111116 % = 0
1111117 % = 0
1111118 % = 6
1111119 % = 6
11111111 % = 0
11111112 % = 0
11111113 % = 1
11111114 % = 2
11111115 % = 0
11111116 % = 4
11111117 % = 3
11111118 % = 6
11111119 % = 7
111111111 % = 0
111111112 % = 0
111111113 % = 2
111111114 % = 2
111111115 % = 0
111111116 % = 2
111111117 % = 5
111111118 % = 6
111111119 % = 8
1111111111 % = 0
1111111112 % = 0
1111111113 % = 0
1111111114 % = 2
1111111115 % = 0
1111111116 % = 0
1111111117 % = 4
1111111118 % = 6
1111111119 % = 0
1 /*
2 * SOUR:sgu169
3 * ALGO:math
4 * DATE: 2009年 11月 29日 星期日 11:11:37 CST http://www.cppblog.com/schindlerlee
5 * COMM:2
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 using namespace std;
13 typedef long long LL;
14 const int maxint = 0x7fffffff;
15 const long long max64 = 0x7fffffffffffffffll;
16
17 int n;
18 int main()
19 {
20 int i,j,pre = 1;
21 scanf("%d",&n);
22 if(n == 1) {
23 printf("8\n");
24 }else {
25 int res = 1;
26 if((n-1) % 3 == 0) res +=2;
27 if((n-1) % 6 == 0) res ++;
28 printf("%d\n",res);
29 }
30
31 return 0;
32 }
33
给出n个物品,判断是否有超过一半的物品是相同的。
前提是,两个物品只有放到一个特殊的装置中才能判断是否相同。
Θ(n^2):brute force
对每一个物体遍历
Θ(nlogn):分治,下面的代码纯属表达思想用,没有测试!!!
int divide(int *a,int n) { if(n == 2) { if(a[0] == a[1]) { return a[0]; } return EMPTY; } int ca = divide(a,n/2); int cb = divide(a + n/2.n - n/2); if(ca != EMPTY) { if(ca is majority in a[n/2 ... n-n/2]) { return ca; } } if(cb != EMPTY) { if(cb is majority in a[0...n/2]) { return cb; } } return EMPTY; }Θ(n):规模下降
Lemma:如果两个物品不同那么在去掉这两个物品的剩余物品中,如果存在Majority
元素,那么这个元素也是去掉之前的解.
设考虑要去掉的两个物品是A,B
如果A,B都不是Majority元素,那么在去掉A,B之后Majority元素一定不变
如果A是Majority元素,那么去掉两个元素之后,在n-2个物品中原来的Majority物品个数
由n/2 + 1变为 n/2,依然在n-2个物品中占大多数
贴<<Algorithms Design Techniques and Analysis>>上的代码,哥亲自输入的,
我的技术博客http://www.cppblog.com/schindlerlee
Algorithm 5.9 MAJORITYInput:An array A[1...n] of n elements.Output:The majority element if it exists:otherwise non. 1. c ← candidate(1) 2. cout ← 0; 3. for j ← 1 to n 4. if A[j] == c then count ← count + 1 5. end for 6. if count > ⌊n/2⌋ then return c 7. else return none 8. 9. Procedure candidate(m)10. j ← m;c ← A[m];count ← 111. while j < n and count > 012. j ← j + 113. if A[j] == c then count ← count + 114. else count ← count - 115. end while16. if j == n then return c17. else return candidate(j + 1)
最短路的变形,题意比较简单,具体看代码
1 /*
2 * SOUR:pku 2353
3 * ALGO:dp
4 * DATE: 2009年 12月 12日 星期六 20:05:20 CST
5 * COMM:3
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 #include<queue>
13 using namespace std;
14 typedef long long LL;
15 const int maxint = 0x7fffffff;
16 const long long max64 = 0x7fffffffffffffffll;
17 const int N = 512;
18 const int inf = 100000001;
19 int m,n,x,y;
20 int g[N][N],out[N*N],top,dis[N][N],vis[N][N],pre[N][N][2];
21
22 struct Path
23 {
24 int x,y;
25 int len;
26 Path(){}
27 Path(int a,int b,int c) { x = a,y = b,len = c;}
28 friend bool operator < (Path a,Path b) {
29 return a.len > b.len;
30 }
31 };
32
33 int search()
34 {
35 int i,j,k;
36 for(i = 1;i < m;i++) {
37 for(j = 0;j < n;j++) {
38 dis[i][j] = maxint;
39 }
40 }
41 for(i = 0;i < n;i++) {
42 dis[0][i] = g[0][i];
43 }
44 priority_queue<Path> que;
45 for(i = 0;i < n;i++) {
46 que.push(Path(0,i,g[0][i]));
47 }
48
49 int sum;
50 int res = maxint;
51 while(!que.empty()) {
52 Path u = que.top(); que.pop();
53 if(u.x == m - 1) {
54 if(u.len < res) {
55 res = u.len;
56 x = u.x;
57 y = u.y;
58 continue;
59 }
60 }
61 if(u.len != dis[u.x][u.y])
62 continue;
63
64 if (dis[u.x +1][u.y] > u.len + g[u.x+1][u.y]) {
65 dis[u.x +1][u.y] = u.len + g[u.x+1][u.y];
66 que.push(Path(u.x + 1,u.y,u.len + g[u.x+1][u.y]));
67 pre[u.x+1][u.y][0] = u.x;
68 pre[u.x+1][u.y][1] = u.y;
69 }
70
71 i = u.y - 1;
72 if(i >= 0 && i < n) {
73 sum = g[u.x][i];
74 if (dis[u.x][i] > u.len + sum) {
75 dis[u.x][i] = u.len + sum;
76 que.push(Path(u.x,i,u.len + sum));
77 pre[u.x][i][0] = u.x;
78 pre[u.x][i][1] = u.y;
79 }
80 }
81
82 i = u.y + 1;
83 if(i >= 0 && i < n) {
84 sum = g[u.x][i];
85 if (dis[u.x][i] > u.len + sum) {
86 dis[u.x][i] = u.len + sum;
87 que.push(Path(u.x,i,u.len + sum));
88 pre[u.x][i][0] = u.x;
89 pre[u.x][i][1] = u.y;
90 }
91 }
92 }
93 return sum;
94 }
95
96 int main()
97 {
98 int i,j,k;
99 scanf("%d%d",&m,&n);
100 for(i = 0;i < m;i++) {
101 for(j = 0;j < n;j++) {
102 scanf("%d",&g[i][j]);
103 pre[i][j][0] = -1;
104 pre[i][j][1] = -1;
105 }
106 }
107
108 int res = search();
109 //printf("%d\n",res);
110 int tx,ty;
111 while(x != -1 && y != -1) {
112 out[top++] = y;
113 tx = pre[x][y][0];
114 ty = pre[x][y][1];
115 x = tx,y = ty;
116 }
117 for(i = top - 1;i >= 0;i--) {
118 printf("%d\n",out[i] + 1);
119 }
120 return 0;
121 }
122
123