#
简单的树形动态规划
贴代码
1 /*
2 * SOUR:sgu 134
3 * ALGO:tree dp
4 * DATE: 2009年 12月 09日 星期三 16:28:16 CST
5 * COMM:3
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 #include<vector>
13 using namespace std;
14 typedef long long LL;
15 const int maxint = 0x7fffffff;
16 const long long max64 = 0x7fffffffffffffffll;
17 const int N = 16100;
18 #define pb(x) push_back(x)
19 vector<int> g[N];
20 int vis[N];
21 int n,res = maxint,out[N],top;
22 void ckmax(int &a,int b) { if(a < b) a = b;}
23 int dfs(int u)
24 {
25 //printf("dfs = %d\n",u);
26 vis[u] = true;
27 int sum = 0,val = 0,tmp;
28 for(int i = 0;i < g[u].size();i++) {
29 int v = g[u][i];
30 if(!vis[v]) {
31 tmp = dfs(v);
32 sum += tmp;
33 ckmax(val,tmp);
34 }
35 }
36 tmp = n - 1 - sum;
37 ckmax(val,tmp);
38 if (res > val) {
39 res = val,top = 1,out[0] = u;
40 }else if(val == res) {
41 out[top++] = u;
42 }
43 return sum + 1;
44 }
45
46 int main()
47 {
48 int i,j,k,a=-1,b;
49 scanf("%d",&n);
50 for(i = 1;i < n;i++) {
51 scanf("%d%d",&a,&b);
52 g[a].pb(b);
53 g[b].pb(a);
54 }
55 if(a != -1) {
56 dfs(a);
57 printf("%d %d\n",res,top);
58 sort(out,out + top);
59 if(top > 0) printf("%d",out[0]);
60 for(i = 1;i < top;i++) {
61 printf(" %d",out[i]);
62 }
63 putchar(10);
64 }else {
65 printf("0 0\n");
66 }
67 return 0;
68 }
69
70
sgu133 排序,看你几分钟能想出来
1 scanf("%d",&n);
2 for(i = 0;i < n;i++) {
3 scanf("%d%d",&a[i].l,&a[i].r);
4 }
5 sort(a,a + n,cmp);
6 int res = 0,pre = -1;
7 for(i = 0;i < n;i++) {
8 if(a[i].r < pre) {
9 res ++;
10 }
11 pre = max(pre,a[i].r);
12 }
13 printf("%d\n",res);
14
sgu181 算一个递推式的第k项,很容易错
1 /*
2 * SOUR:sgu181
3 * ALGO:math
4 * DATE: 2009年 12月 11日 星期五 21:50:18 CST
5 * COMM:3
6 * 注意k可能出现在循环节开始之前
7 * */
8 #include<iostream>
9 #include<cstdio>
10 #include<cstdlib>
11 #include<cstring>
12 #include<algorithm>
13 using namespace std;
14 typedef long long LL;
15 const int maxint = 0x7fffffff;
16 const long long max64 = 0x7fffffffffffffffll;
17
18 LL A,alpha,beta,gamma,M,k;
19 const int N = 20010;
20 LL vis[N];
21 LL val[N];
22 int main()
23 {
24 LL i;
25 /*
26 1) x0 = A;
27 2) xi = (alpha * x(i-1)^2 + beta * x(i-1) + gamma) mod M, for i >= 1.
28 * */
29 //A (1 <= A <= 10000), alpha (0 <= alpha <= 100), beta (0 <= beta <= 100), gamma
30 //(0 <= gamma <= 100), M (1 <= M <= 1000), k (0 <= k <= 10^9)
31
32 fill(vis,vis + N,-1);
33 cin >> A >> alpha >> beta >> gamma >> M >> k;
34 LL xi = A,step = 0,cycle,before;
35 while(1) {
36 if(vis[xi] >= 0) {
37 cycle = step - vis[xi];
38 before = vis[xi];
39 break;
40 }
41 val[step] = xi;
42 vis[xi] = step ++;
43
44 xi = (alpha * xi*xi + beta * xi + gamma) % M;
45 }
46 if(k < step ) {
47 cout << val[k] << endl;
48 }else {
49 LL idx = (k-before)%cycle + before;
50 cout << val[idx] << endl;
51 }
52
53 return 0;
54 }
55
56
2009年12月8日星期二.sgu482
sgu482:dp
题目解释:n个木条,高h[1...n],要求拿走尽量多的木条,同时保证此时剩下的所有木条的周长
不小于原来的一半
从反面思考,题目要求求能拿走的最大面积,按照周长dp没有办法。搜是肯定不行的,可以按照
面积dp,面积最大才5000。
我们可以求出每个面积的最大周长,遍历一下找符合条件的最小面积,然后用原面积减这个面积
即是所求。
现在考虑求周长的问题
如果后一个比上一个短 周长 += 2 ;
| | || |如果后一个比上一个长 周长 += 2 + 2 * abs(h[i]-h[i-1]);
|| || |但是如果按照如上的思路,肯定会写出一个2维dp,例如
area[i] 表示面积为i时的最大周长
1
2 for(i = 1;i <= n;i++) {
3 for(s = h[i];s <= 5000;s++) {
4 if(area[s-h[i]] >= 0 ) {
5 if (area[s] < area[s-h[i]] + cacu(h[i],last[s-h[i]])) {
6 area[s] = area[s-h[i]] + cacu(h[i],last[s-h[i]]));
7 last[s] = h[i];
8 }
9 }
10 }
11 }
但是这样写是错的.... 我一开始就是这么写的 WA at test case 13
∵ 当前面积的<<<更大周长并不能保证更大面积得到更好的解>>>,周长只和高度的差有关
<<<也就是二维dp并不具有最优子结构>>>
∴ 要写成三维dp
dp[i][j]表示面积为i时使用前j个木条的周长最大值
如下方法能求出最优解
1 for(i = 1;i <= n;i++) {
2 for(s = h[i];s < N;s++) {
3 for(j = i - 1;j >= 0;j --) {
4 if(dp[s-h[i]][j] >= 0) {
5 if (dp[s][i] < dp[s-h[i]][j] + cacu(h[i],h[j])) {
6 dp[s][i] = dp[s-h[i]][j] + cacu(h[i],h[j]);
7 }
8 }
9 }
10 }
11 }
==========贴代码====================华丽丽的分割线====================
1 /*
2 * SOUR:sug482
3 * ALGO:dp
4 * DATE: 2009年 12月 05日 星期六 13:19:59 CST
5 * COMM:3~4
6 * 从反面思考
7 * */
8 #include<iostream>
9 #include<cstdio>
10 #include<cstdlib>
11 #include<cstring>
12 #include<algorithm>
13 using namespace std;
14 typedef long long LL;
15 const int maxint = 0x7fffffff;
16 const long long max64 = 0x7fffffffffffffffll;
17 const int N = 5010;
18 const int inf = 1 << 28;
19 int n;
20 int dp[N][128],pre[N][128][2],h[N],perimeter,area,res,out[N],top,vis[128];
21 int cacu(int h, int last) { return h-last+abs(h-last)+2; }
22
23 int main()
24 {
25 int i,j,k,s,x,y;
26 scanf("%d",&n);
27 h[0] = 0,perimeter = 0,area = 0,res = 0;
28 for(i = 1;i <= n;i++) {
29 scanf("%d",h + i);
30 perimeter += cacu(h[i],h[i-1]);
31 area += h[i];
32 }
33 for(i = 0;i < N;i++) {dp[0][i] = 0;}
34 for(i = 1;i < N;i++) {
35 for(j = 0;j < N;j++) {
36 dp[i][j] = -1;
37 }
38 }
39 for(i = 1;i <= n;i++) {
40 for(s = h[i];s < N;s++) {
41 for(j = i - 1;j >= 0;j --) {
42 if(dp[s-h[i]][j] >= 0) {
43 if (dp[s][i] < dp[s-h[i]][j] + cacu(h[i],h[j])) {
44 dp[s][i] = dp[s-h[i]][j] + cacu(h[i],h[j]);
45 pre[s][i][0] = s - h[i];
46 pre[s][i][1] = j;
47 }
48 }
49 }
50 if(dp[s][i] + dp[s][i] >= perimeter) {
51 if (res < area - s) {
52 res = area - s;
53 x = s,y = i;
54 }
55 }
56 }
57 }
58 printf("%d\n",res);
59 if(res > 0) {
60 while(x != 0 && y != 0) {
61 vis[y] = 1;
62 int tx = pre[x][y][0];
63 int ty = pre[x][y][1];
64 x = tx,y = ty;
65 }
66 for(i = 1;i <= n;i++) {
67 if(!vis[i]) {
68 out[top++] = i;
69 }
70 }
71 }
72 printf("%d\n",top);
73 if(top > 0)
74 printf("%d",out[0]);
75 for(i = 1;i < top;i++) {
76 printf(" %d",out[i]);
77 }
78 if(top > 0)
79 putchar(10);
80 return 0;
81 }
82
1 /*
2 * SOUR:sgu130
3 * ALGO:catalan数看组合数学的证明
4 * DATE: 2009年 12月 07日 星期一 16:34:54 CST
5 * COMM:2
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 using namespace std;
13 typedef long long LL;
14 const int maxint = 0x7fffffff;
15 const long long max64 = 0x7fffffffffffffffll;
16
17 LL n,res,F[32];
18 LL f(LL s)
19 {
20 if(F[s] != 0) {
21 return F[s];
22 }
23 if(s == 0) {
24 return 1;
25 }
26
27 LL sum = 0;
28 for(LL i = 0;i < s;i++) {
29 sum += f(i) * f(s - i - 1);
30 }
31 return (F[s] = sum);
32 }
33
34 int main()
35 {
36 memset(F,0,sizeof(F));
37 cin >> n;
38 cout << f(n) << ' ' << n + 1 <<endl;
39 return 0;
40 }
41
42
43
1 /*
2 * SOUR:sgu126
3 * ALGO:模拟
4 * DATE: 2009年 12月 07日 星期一 00:29:29 CST
5 * COMM:3
6 * 看ACRush写的报告说是模拟,然后我模拟了以下,TLE了,然后开始分析
7 * 两个数a,b除完gcd(a,b)之后
8 * a == 1,b == 1,乘2之后向上推导
9 * a == 2,b == 2,的上一步只可能是a == 3,b == 1,之后继续乘2向上导
10 * 可以发现只有a是b的
11 * 1 3 7 15 31 63 127  倍时能得出b == 0
倍时能得出b == 0
12 * 此时把a+b必须是2的整数倍才行,而这个倍数就是答案
13 * */
14 #include<iostream>
15 #include<cstdio>
16 #include<cstdlib>
17 #include<cstring>
18 #include<algorithm>
19 using namespace std;
20 typedef long long LL;
21 const int maxint = 0x7fffffff;
22 const long long max64 = 0x7fffffffffffffffll;
23
24 int gcd(int a, int b)
25 {
26 if (b == 0) return a;
27 return gcd(b,a%b);
28 }
29
30 int a,b;
31 int main()
32 {
33 int i,j,k;
34 cin >> a >> b;
35 if(a < b) { swap(a,b); }
36 int tmp = gcd(a,b),sum,bit = 0,idx = 0;
37 a /= tmp,b /= tmp;
38 sum = a + b;
39 for(i = 0;i < 32;i++) {
40 if(sum &(1 << i)) {
41 bit ++;
42 idx = i;
43 }
44 }
45 if(bit == 1) {
46 printf("%d\n",idx);
47 }else {
48 printf("-1\n");
49 }
50 return 0;
51 }
52
53
54
2009年12月6日星期日.sgu124
sgu124:判断点在多边形内还是外还是边上
由于线段是随机给出的,没有顺时针或者逆时针顺序,所以转角法是不能用的
主要考虑射线法
射线法可以参考黑数P379,有详细的讲解,也很好理解
trick
1.要注意平行线段的处理,其实出现射线穿过线段端点的情况,完全和可以忽略
2.判断线段和射线相交时,要注意判断交点是不是在射线上也就是
对于射线L:P0 + s*v ,(s >= 0) 要注意判断交点在s >= 0时才算相交
其他就没有了。
做sgu的题真锻炼,已经很久没期待过1Y了...
1
2 /*
3 * SOUR:sgu124
4 * ALGO:computational geometry
5 * DATE: 2009年 12月 06日 星期日 20:50:13 CST
6 * COMM:3
7 * */
8 #include<iostream>
9 #include<cstdio>
10 #include<cstdlib>
11 #include<cstring>
12 #include<algorithm>
13 using namespace std;
14 typedef long long LL;
15 const int maxint = 0x7fffffff;
16 const long long max64 = 0x7fffffffffffffffll;
17
18 const int N = 10100;
19 const double eps = 1e-10;
20 int dcmp(double x) { return (x > eps) - (x < -eps);}
21 struct point_t {
22 double x, y;
23 point_t (){}
24 point_t (double a,double b){x = a,y = b;}
25 }p[N][2],core;
26 point_t operator + (point_t a,point_t b) { return point_t(a.x + b.x,a.y + b.y);}
27 point_t operator - (point_t a,point_t b) { return point_t(a.x - b.x,a.y - b.y);}
28 double dot_mul(point_t a,point_t b) { return a.x * b.x + a.y * b.y;}
29 double cross_mul(point_t a,point_t b) { return a.x * b.y - a.y * b.x;}
30 double cross_mul(point_t a,point_t b,point_t c) { return cross_mul(a-c,b-c);}
31 double dist2(point_t a,point_t b) { return (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y);}
32
33 bool judge(point_t a,point_t b,point_t c,point_t d)
34 {
35 if(dcmp(cross_mul(a-c,d-c)) * dcmp(cross_mul(b-c,d-c)) < 0) {
36 if(dcmp(cross_mul(a-b,c-b)) > 0) //射线端
37 return true;
38 }
39 return false;
40 }
41
42 int n;
43 bool rel(point_t a,point_t b,point_t c)
44 //a 和线段bc
45 {
46 double tmp =(dot_mul(a-b,c-b) / dist2(b,c)) ;
47 //printf("rel = %f\n",tmp);
48 return tmp >= 0 && tmp <= 1;
49 }
50
51 void work()
52 {
53 int sum = 0;
54 point_t to = core;
55 to.x += 1;//随便取的射线
56 to.y += 7;
57 for(int i = 0;i < n ;i++) {
58 if(0 == dcmp(cross_mul(p[i][1] - p[i][0],core-p[i][0])) &&
59 rel(core,p[i][0],p[i][1])) {
60 printf("BORDER\n");
61 return;
62 }
63 if(judge(p[i][0],p[i][1],core,to))
64 sum++;
65 }
66 //printf("sum=%d\n",sum);
67 if(sum & 1) {
68 printf("INSIDE\n");
69 }else {
70 printf("OUTSIDE\n");
71 }
72 }
73
74 int main()
75 {
76 int i,j,k;
77 scanf("%d",&n);
78 for(i = 0;i < n;i++) {
79 scanf("%lf%lf%lf%lf",&p[i][0].x,&p[i][0].y,&p[i][1].x,&p[i][1].y);
80
81 if(p[i][0].y < p[i][1].y) { //保证线段总是指向左上的
82 swap(p[i][0],p[i][1]);
83 }else if(p[i][0].y == p[i][1].y && p[i][0].x > p[i][1].x) {
84 swap(p[i][0],p[i][1]);
85 }
86 }
87 scanf("%lf%lf",&core.x,&core.y);
88 work();
89 return 0;
90 }
91
92
2009年12月4日星期五.sgu103==pku1158
sgu103:dijkstra
最好自己琢磨以下怎么做
动态dijkstra
trick:
注意两个顶点之间虽然有可能有路,但是由于信号灯的周期有可能永远也不通
sgu上不仅要数出最短路的值还要求输出这条路径。
1
2 const int N = 320;
3 const int inf = 1 << 30;
4 int g[N][N];
5 struct color{
6 int t,c;
7 color(){}
8 };
9 const int BLUE = 1;
10 const int PURPLE = 0;
11 struct node {
12 bool isblue;
13 int tb,tp,rt;
14 node() {}
15 color getColor(int time);
16 }jun[N];
17
18 color node::getColor(int time)
19 {
20 color ret;
21 if(time < rt) {
22 ret.c = isblue;
23 ret.t = rt - time;
24 }else {
25 int cycle = tb + tp;
26 time = (time - rt) % cycle;
27 if(isblue) {
28 if(time < tp) {
29 ret.c = PURPLE;
30 ret.t = tp - time;
31 }else {
32 ret.c = BLUE;
33 ret.t = cycle - time;
34 }
35 }else {
36 if(time < tb) {
37 ret.c = BLUE;
38 ret.t = tb - time;
39 }else {
40 ret.c = PURPLE;
41 ret.t = cycle - time;
42 }
43 }
44 }
45 return ret;
46 }
47
48 int src,dest,m,n,dis[N],pre[N],out[N],top;
49 bool vis[N];
50
51 int time2go(int i,int j,int now,int cnt)
52 {
53 if(cnt > 3) { return inf;}
54 color c1 = jun[i].getColor(now);
55 color c2 = jun[j].getColor(now);
56 if(c1.c == c2.c) {
57 return now;
58 }
59 if(c1.t == c2.t) {
60 return time2go(i,j,now + c1.t,cnt+1);
61 }
62 return now + min(c1.t,c2.t);
63 }
64
65 bool dijkstra()
66 {
67 int i,j,k;
68 memset(vis,0,sizeof(vis));
69 memset(pre,0,sizeof(pre));
70 for(i = 1;i <= n;i++) {
71 dis[i] = inf;
72 }
73 dis[src] = 0;
74 for(k = 1;k <= n;k++) {
75 int idx = 0,val = inf;
76 for(i = 1;i <= n;i++) {
77 if(dis[i] < val && vis[i] == 0) {
78 val = dis[i],idx = i;
79 }
80 }
81 if(idx == 0) {
82 return false;
83 }
84 vis[idx] = 1;
85 for(i = 1;i <= n;i++) {
86 if(vis[i] == false && g[idx][i] < inf){
87 int tmp =time2go(idx,i,dis[idx],0);
88 if(tmp < inf) {
89 int wei =tmp + g[idx][i];
90 if (dis[i] > wei) {
91 dis[i] = wei;
92 pre[i] = idx;
93 }
94 }
95 }
96 }
97 }
98
99 if(dis[dest] >= inf) {
100 return false;
101 }else {
102 printf("%d\n",dis[dest]); top = 0;
103 int tmp = dest;
104 while(tmp > 0) {
105 out[top++] = tmp;
106 tmp = pre[tmp];
107 }
108 for(i = top - 1;i > 0;i--) {
109 printf("%d ",out[i]);
110 }
111 printf("%d\n",out[0]);
112 }
113 return true;
114 }
115
116 int main()
117 {
118 int i,j,k;
119 char s[16];
120 scanf("%d%d",&src,&dest);
121 scanf("%d%d",&n,&m);
122 for(i = 1;i <= n;i++) {
123 scanf("%s %d %d %d\n",s,&jun[i].rt,&jun[i].tb,&jun[i].tp);
124 jun[i].isblue = (s[0] == 'B');
125 }
126 for(i = 1;i <= n;i++) {
127 for(j = 1;j <= n;j++) {
128 g[i][j] = inf;
129 }
130 }
131 for(i = 0;i < m;i++) {
132 int a,b,c;
133 scanf("%d%d%d",&a,&b,&c);
134 g[a][b] = g[b][a] = c;
135 }
136 if(dijkstra() == false) {
137 printf("0\n");
138 }
139 return 0;
140 }
141
搬家到
http://www.cnblogs.com/schindlerlee/
1.想要代码的可以email我
2.分享你的知识
3.尊重他人的隐私
4.给自己网上留个好印象
5.平心静气地争论
6.尊重别人的时间和带宽
7.本人坚持原创,转载请注明出处。
2009年11月30日星期一.sgu110
sgu110:完全被这题玩了。。。
题意很简单:
一堆球,一条光线,光线反射符合反射定律,输出所有反射经过的球的序号
的确没有光线的起点在球中。
tricks:
1. test case 3 是无交点的。。。。我被这个玩了
2. 直线要表示成参数方程
P = P0 + s*v; 注意是射线,所以只有 "s >= 0" 时是成立的,注意 >= 0,自己想下为什么有等于0
还要特判一下不能连着交同一个圆
貌似没有别的问题了
反射直线有两个推法
1.
lt表示直线的参数方程
lt.p 为p0,lt.v为v
point_t v = normal(tmp - circles[idx]);
double d = -(tmp.x * v.x + tmp.y * v.y + tmp.z * v.z); //平面方程ax + by + cz + d = 0中的d
double dis = fabs(p2p(lt.p, v.x, v.y, v.z, d)); // p2p为点到平面的距离
v = tmp - lt.p + scale(v, dis * 2);
lt.p = tmp, lt.v = normal(v);
下图表示了上面求解的过程
\ | / \ | / \|/ --------- \ \ \ 还可以跟据,
2.
求出中点,mid = (s1 + s2)/2;
然后求出s2即可
\ * / \ / \ /==============================华丽丽的分割线==============================
贴代码
1 /*
2 * SOUR:sgu110
3 * ALGO:3D computational geometry
4 * DATE: 2009年 11月 29日 星期日 17:21:22 CST
5 * COMM:4
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 #include<cmath>
13 using namespace std;
14 typedef long long LL;
15 const int maxint = 0x7fffffff;
16 const long long max64 = 0x7fffffffffffffffll;
17 const int N = 128;
18 int n;
19 struct point_t {
20 double x,y,z,r;
21 point_t(){}
22 point_t(double a,double b,double c){x = a,y = b,z = c;}
23 }circle[N],s,e;
24 point_t operator + (point_t a,point_t b) { return point_t(a.x + b.x ,a.y + b.y,a.z + b.z);}
25 point_t operator - (point_t a,point_t b) { return point_t(a.x - b.x ,a.y - b.y,a.z - b.z);}
26 point_t scale(point_t a,double fac) { return point_t(a.x * fac,a.y * fac,a.z * fac);}
27 double dist(point_t a) { return sqrt(a.x * a.x + a.y * a.y + a.z * a.z);}
28 point_t normal(point_t a) {
29 double len = dist(a);
30 return point_t(a.x / len,a.y/len,a.z/len);
31 }
32 point_t setLen(point_t a,double fac) {
33 a = normal(a);
34 return point_t(a.x*fac,a.y*fac,a.z*fac);
35 }
36 int out[N*N],top;
37
38 double p2p(point_t p,double a,double b,double c,double d)
39 {
40 return (a * p.x + b * p.y + c * p.z + d)/sqrt(a * a + b * b + c* c);
41 }
42
43 const double inf = 1e10;
44 const double eps = 1e-12;
45 double dot_mul(point_t a,point_t b) {
46 return a.x * b.x + a.y * b.y + a.z * b.z;
47 }
48 void solve()
49 {
50 int i,j,k,pre = -1;
51 top = 0;
52 for(k = 0;k < 12;k++) {
53 int idx = 0;
54 double mink = inf;
55 for(i = 1;i <= n;i++) {
56 if(pre != i) {
57 double a = (e.x * e.x + e.y * e.y + e.z * e.z);
58 point_t t = s - circle[i];
59 double b = 2 * dot_mul(e,t);
60 double c = t.x * t.x + t.y * t.y + t.z * t.z - circle[i].r * circle[i].r;
61 if(b * b >= 4 * a * c) {
62 double s1 = (-b - sqrt(b*b - 4 * a*c))/(2*a);
63 double s2 = (-b + sqrt(b*b - 4 * a*c))/(2*a);
64 if(s1 >= 0) {
65 if(s1 < mink) {
66 mink = s1;
67 idx = i;
68 }
69 }else if(s2 >= 0){
70 if(s2 < mink) {
71 mink = s1;
72 idx = i;
73 }
74 }
75 }
76 }
77 }
78 if(idx > 0) {
79 point_t p = s + scale(e,mink);
80 //p is the point which intersects with the circles
81 point_t v = normal(p - circle[idx]); // normal vector
82 double d = -dot_mul(p,v);
83 //double dis = fabs(p2p(s,v.x,v.y,v.z,d));
84 double dis = fabs(dot_mul(v,s)+d);
85
86 point_t mid = p + scale(v,dis);
87 point_t p1 = scale(mid,2) - s;
88
89 s = p,e =p1-p;
90 out[top++] = idx;
91 pre = idx;
92 }else {
93 break;
94 }
95 }
96 if(top > 0) //哥死在这句话上了。。。
97 printf("%d",out[0]);
98 for(i = 1;i < 10 && i < top;i++) {
99 printf(" %d",out[i]);
100 }
101 if(top > 10) {
102 printf(" etc.");
103 }
104 putchar(10);
105 }
106
107 int main()
108 {
109 int i,j,k;
110 while(scanf("%d",&n) == 1) {
111 top = 0;
112 for(i = 1;i <= n;i++) {
113 scanf("%lf%lf%lf%lf",&circle[i].x,&circle[i].y,&circle[i].z,&circle[i].r);
114 }
115 scanf("%lf%lf%lf%lf%lf%lf",&s.x,&s.y,&s.z,&e.x,&e.y,&e.z);
116 e = e - s;
117 solve();
118 }
119 return 0;
120 }
121
2009年11月25日星期三.sgu106
这题终于过了......
太容易错了
忘了sgu是ms win,用%lld错了十几次,干脆cin就得了,I64d在linux又编译不了
106. The equation
There is an equation ax + by + c = 0. Given a,b,c,x1,x2,y1,y2 you must determine, how
many integer roots of this equation are satisfy to the following conditions :
x1<=x<=x2, y1<=y<=y2. Integer root of this equation is a pair of integer numbers
(x,y).
Input
Input contains integer numbers a,b,c,x1,x2,y1,y2 delimited by spaces and line breaks.
All numbers are not greater than 108 by absolute value.
Output
Write answer to the output.
Sample Input
1 1 -3
0 4
0 4
Sample Output
4
首先在开始正式讲解之前我要说,原来除法不一定是下取整的。。。。
比如 1 / 2 = 0
但是-1 / 2 = 0;
所以我们要自己写上取整和下取整的函数
看到zzy的一个写法,很不错,见代码中的upper和lower
直线可以写成参数方程的模式
L1: p0 + t * v; t为实数,v 为直线的方向向量
ax + by + c = 0;
首先可以把c移到右边
ax + by = -c;
知道a,b可以利用扩展欧几里德公式求出p0和d,(d = gcd(a,b))
如果c不能整除d的话就没有整数解,这点是显然的,可以简单思考一下.
另外通过直线的几何意义可以知道
v = (b ,-a)或
v = (-b, a)
取其中一个即可
tx = (x - x0)/b;
ty = (y - y0)/-a;
通过两个去见求出tmin,tmax,之后
ans = tmax - tmin + 1就是结果,如果ans < 0 就是无解
此题破例贴代码
1
2 LL ans = 0;
3 LL kmin = -300000000000000000LL, kmax = 300000000000000000LL;
4
5 LL ext_gcd(LL a, LL b, LL & x, LL & y)
6 {
7 if (b == 0) {
8 x = 1;
9 y = 0;
10 return a;
11 } else {
12 LL d = ext_gcd(b, a % b, x, y);
13 LL t = x;
14 x = y;
15 y = t - a / b * y;
16 return d;
17 }
18 }
19
20 LL upper(LL a, LL b)
21 {
22 if (a <= 0)
23 return a / b;;
24 return (a - 1) / b + 1;
25 }
26
27 LL lower(LL a, LL b)
28 {
29 if (a >= 0)
30 return a / b;
31 return (a + 1) / b - 1;
32 }
33
34 void update(LL L, LL R, LL a)
35 {
36 if (a < 0) {
37 L = -L;
38 R = -R;
39 a = -a;
40 swap(L, R);
41 }
42 kmin = max(kmin, upper(L, a));
43 kmax = min(kmax, lower(R, a));
44 }
45
46 int main()
47 {
48 LL a, b, c, x1, x2, y1, y2, x0, y0;
49 cin >> a >> b >> c >> x1 >> x2 >> y1 >> y2; // sgu 是ms win,应该用%I64d,我错了20几次才发现 .
.
50 c = -c,ans = 0;
51 if (a == 0 && b == 0) {
52 if (c == 0)
53 ans = (LL) (x2 - x1 + 1) * (y2 - y1 + 1);
54 } else if (a == 0) {
55 LL t = c / b;
56 ans = (c % b == 0 && t <= y2 && t >= y1) * (x2 - x1 + 1);
57 } else if (b == 0) {
58 LL t = c / a;
59 ans = (c % a == 0 && t <= x2 && t >= x1) * (y2 - y1 + 1);
60 } else {
61 LL d = ext_gcd(a, b, x0, y0);
62 if (c % d == 0) {
63 LL p = c / d;
64 update(x1 - p * x0, x2 - p * x0, b / d);
65 update(y1 - p * y0, y2 - p * y0, -a / d);
66 ans = kmax - kmin + 1;
67 if (ans < 0) ans = 0;
68 }
69 }
70 cout << ans << endl;
71 return 0;
72 }
73
74
2009年11月22日星期日.sgu154 sgu175sgu154:非常好的数论+二分题目 You task is to find minimal natural number N, so that N! contains exactly Q zeroes on the trail in decimal notation. As you know N! = 1*2*...*N. For example, 5! = 120, 120 contains one zero on the trail.InputOne number Q written in the input (0<=Q<=10^8).OutputWrite "No solution", if there is no such number N, and N otherwise.Sample test(s) Input 2Output 10首先要明白一件事x!末尾的0的个数至于2和5的个数有关,又因为2的个数已经多余5,所以阶乘末尾0的个数完全等价于所有数中5的个数所以阶乘末尾0的个数可以用如下函数计算int count(int x) //count the num of 0s in x!{ int res = 0; while(x > 0) { res += x / 5; x /= 5; } return res;}然后题目要求末尾个数有n个0的x!中,x为多少因为哦count函数具有单调增加的性质,所以完全可以二分寻找符合条件的xtrick 1.n == 0 ,时答案是1trick 2.二分出来的结果有可能应该输出No Solution !(具体原因自己考虑一下)sgu175:经典 Let phi(W) is the result of encoding for algorithm:1. If the length of W is 1 then phi(W) is W;2. Let coded word is W = w1w2...wN and K = N / 2 (rounded down);3. phi(W) = phi(wNwN-1...wK+1) + phi(wKwK-1...w1).For example, phi('Ok') = 'kO', phi('abcd') = 'cdab'.Your task is to find position of letter wq in encoded word phi(W).InputGiven integers N, q (1 <= N <= 10^9; 1<= q <= N), where N is the length of word W.OutputWrite position of letter wq in encoded word phi(W).Input 9 4Output 8读完题之后,直觉的想法就是递归模拟,复杂度也对,也没问题,但是就是很容易错,编码困难.要跟据level的奇偶性,分别讨论,有兴趣可以尝试一下,我没成功......google 了以下发现了一个很好的想法,以下是我跟据那个想法写的递归版本LL n, q;int bin(LL n, LL q){ if(n <= 1) return 1; LL k = n / 2; if (q > k) { return bin(n - k, n - q + 1); } else { return n - k + bin(k, k - q + 1); }}以如下为例,解释以下算法 分裂 abcdefghi 时 /\ / \ ihgfe dcba 对于一个n,k = n / 2: 如果 q <= k,这时abcd被倒置,如果要在dcba中找d,等价于在abcd中找a 也就是k到q的距离成为了新的q 如果 q > k,如果要在ihgfe中找h等价于在efghi中寻找f 也就是k到n的距离成为了新的q然后在体会一下上边的算法
2009年11月13日星期五.sgu486 sgu488 sgu496
今天去上午去实验室找老师,下午买了点咳嗽药,睡了很久,晚上查了查明天去北京的路线,
然后才起来今天还没做题....
上次sgu比赛没看到。。。
昨天wanbo说上次比赛中看到大家切题跟切菜一样,于是就看看,挑了三个过的人数多的,
都是简单题,3个1Y,Oh yeah,今天早睡,明天去北京见腾讯校园关系部的那个姐姐..
sgu486: Bulls and Cows简单题
sgu488: Dales and Hills 动态规划
O(n)的扫描,四个数组
LU ^ ^ RU / \ / \ / \ \ / \ / \ / LD v v RD 边界条件考虑好,搞清关系即可
sgu496:496 L-Shapes计算几何
点积判零即可
贴些代码,计算几何苦手可以试试这种风格。
const int N = 5050;struct point_t { //struct 最好加_t以示清晰,加多了就习惯了 int x,y; point_t(){} point_t(int a,int b){x = a,y = b;}}L[N][2];point_t operator + (point_t a,point_t b) { return point_t (a.x + b.x,a.y + b.y);}point_t operator - (point_t a,point_t b) { return point_t (a.x - b.x,a.y - b.y);}bool operator == (point_t a,point_t b) { return a.x == b.x && a.y == b.y;}int dot_mul(point_t a,point_t b) { return a.x * b.x + a.y * b.y;}bool isvertical(point_t a,point_t b,point_t c) { return dot_mul(a-b,b-c) == 0; }
2009年11月12日星期四
今天看MrBayes的源代码了,就A了两道
sgu108:筛法的推广和滚动数组优化
很精简,很强大的一题...
设n为当前数,那么d(n)最大值为 n + 7 * 9所以64大小的数组已经足够
void sieve()
{
int i, j, next;
top = 0;
fill(is_prime, is_prime + 64, 1);
for (i = 1, j = 0; i <= n; i++) {
if (is_prime[i & 63]) {
top++;
while (top == q[j].x) {
q[j++].ans = i;
}
}
next = i + sum[i / 10000] + sum[i % 10000];//预处理sum
is_prime[i & 63] = true;
is_prime[next & 63] = false;
}
}
sgu101:欧拉路
非常强大的一题...
按照题意以骨牌为节点建图的话,题目就变成了hamilton路径搜索。
注意到骨牌的值只有0~6,可以考虑用节点值为节点建图,这样就变成了寻找欧拉路径
注意:
1.判图连通
2.判欧拉回路的存在行
3.如果存在则需要从<存在>的节点开始搜索
4.欧拉回路需要回溯
5.只有一个点的话,无欧拉路,但是有解..
本校同学想要代码的邮件我
sgu的数据太强了,真是太折磨人了
sgu115:calendar
sgu的水题
sgu114:找中位点
算法导论Excercise 9.3-9的题目
看了答案之后我的理解性简单证明:
1.sgu的题目等价于有n个点,每个点有一个人,p个人的话,可以看作是p个坐标相同的点。
2.考虑n的节点个数
设此时的左半边的费用和设为a ,右半边的费用和设为b
如果n是偶数
设最优解坐标为x1,x2
*假设最优解在n / 2 和 n / 2 + 1两个点之间
Cost = a + b;
如果移动最优解的坐标,很容易可以证明
只要坐标还在两个中位点之间,那么解的值就不变。假设在两个中位点之间左移d个单位
Cost = a - (n/2) * d + b + (n/2) * d
= a + b;
右移同理
*假设向左移出了中位点的距离
Cost = a - (n/2-1) * d + b + (n/2-1) * d + x2 - x1 + d
= a + b + d;
如果移动超过这两个点,那么解的值都将变大
如果n是奇数
*设最优解坐标为x,最优值一定在中位点上。
此时Cost = a + b;
*假设最优解左移d个单位
此时Cost = a - (n/2)*d + b + (n/2)*d + d
= a + b + x - d
向右移同理
所以中位点是最优值
114此题就是多了个计数和排序
sgu113:素数
可以发现,只要求sqrt(1000000000) 个素数即可,也就是判断tmp = m / primes[i]
判断tmp是否是素数即可
trick是,tmp可能大于sqrt(1000000000)!!
sgu112:大数幂
sgu111:大数求平方根
方法很多,大多数人都是模拟手算开方,我看了半天没看明白,于是弄了哥迭代法 + java 水过
稍微有一点猥琐...
c++版的求平方根方法
double eps = 1e-8;
int main()
{
int x,i,j,k;
while(scanf("%d",&x) == 1) {
double r = x; //尽量靠近sqrt(x),这里是为了一个通解
double p = 1;
while(p + eps < r) {
r = (r + p) / 2;
p = x / r;
}
printf("%f\n",r);
}
return 0;
}
原版的算法,我改了改
1. Start with an arbitrary positive start value r (the closer to the square root of x, the better).
2. Replace r by the average between r and x/r, that is: (r + x/r) / 2 ,
(It is sufficient to take an approximate value of the average in order to ensure convergence.)
3. Repeat step 2 until r and x/r are as close as desired.
2009年11月10日星期二
首先线性的素数筛法是这么写的
memset(is_prime,1,sizeof(is_prime));
is_prime[1] = 0;
cnt = 0;
for(i = 2;i < M;i++) {
if(is_prime[i]) prime[cnt++] = i;
for(j = 0;j < cnt && i * prime[j] < M;j++) {
is_prime[i * prime[j]] = 0;
if(i % prime[j] == 0) break;
}
}
sgu 118:
1.数学处理之,分解成A1( 1 + A2(1 + A3(1 + A4(......An-1(1 + An))))
2.把数字写出来找规律.
int root(int x)
{
int sum = 各位数字和;
if(sum >= 10)
return root(sum);
return sum;
}
等价于
int root(int x)
{
if(x % 9) return x % 9;
return 9;
}
sgu 117:因数分解,比较大小。
faccnt = 0;
for(i = 0;K > 1 && i < top;i++) {
if(K % prime[i] == 0) {
idx[faccnt++] = i; //tle hint : jump idx
}
while(K % prime[i] == 0) {
fac[i] ++;
K /= prime[i];
}
}
sgu 116:筛法求素数,然后背包,我WA了10几次,
发现题目虽然要求不降序,but,but!!我把结果排序输出的,然后狂WA
去了就OK了。
pku 2850:数学或者几何
没有trcik ,会求两个圆上搭的圆的圆心即可。可以考虑heron公式
挺好的一道计算几何题目
题目大意是:给一条线段代表房子,给一条线段代表路,给一些障碍物,求在路上能完全看到房子的最长连续长度
题目中所有线段都是和x轴平行的
两个难点
1、利用相似三角形,求出再房子和障碍物连线在路上的交点
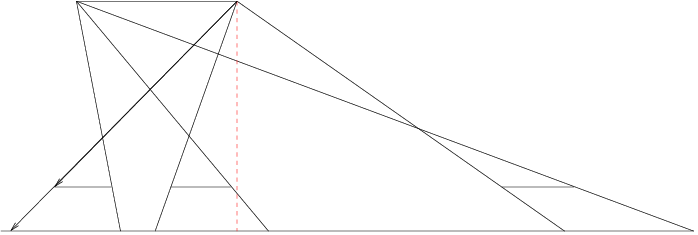
2、判断线段的相交方式,并切割线段
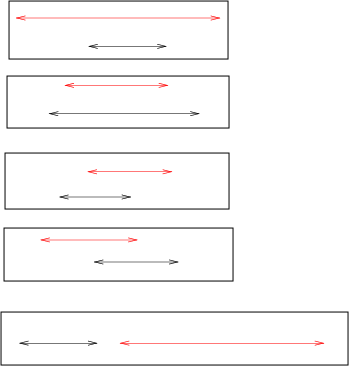
这些问题都解决了之后,就是写代码了
1 /*
2 * SOUR:pku 2074
3 * ALGO:computional geometry
4 * DATE: Thu, 15 Oct 2009 23:22:48 +0800
5 * COMM:3
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 #include<vector>
13 #include<cassert>
14 #include<cmath>
15 using namespace std;
16 typedef long long LL;
17 const int maxint = 0x7fffffff;
18 const long long max64 = 0x7fffffffffffffffll;
19 template<class T>void show(T a, int n){for(int i=0;i<n;++i)cout<<a[i]<<' ';cout<<endl;}
20 template<class T>void show(T a,int r,int l){for(int i=0;i<r;++i)show(a[i],l);cout<<endl;}
21 #define pr(x ) fprintf(stderr, x)
) fprintf(stderr, x)
22 /* #define pr(x ) for(;0;) */
) for(;0;) */
23 const int N = 512;
24 const double eps = 1e-7;
25 struct NODE {
26 double x1,x2,y;
27 NODE(){}
28 NODE(double a,double b){ x1 = a,x2 = b; }
29 }h,ob,root;
30 vector<NODE> g[N];
31 int n,top,pt;
32
33
34 struct point_t{
35 double x,y;
36 point_t(){}
37 point_t(double a,double b){
38 x = a,y = b;
39 }
40 };
41 point_t operator +(point_t a,point_t b) { return point_t(a.x + b.x,a.y + b.y); }
42 point_t operator -(point_t a,point_t b) { return point_t(a.x - b.x,a.y - b.y); }
43 point_t operator *(point_t a,double b) { return point_t(a.x * b,a.y * b); }
44 point_t operator /(point_t a,double b) { return point_t(a.x / b,a.y / b); }
45 double sqr(double x) {return x * x;}
46 double dist(point_t a) { return sqrt(sqr(a.x) + sqr(a.y)); }
47 double dist(point_t a,point_t b) { return dist(a-b); }
48
49 void cut(int idx,double v1,double v2)
50 {
51 int i,j,k;
52 for(i = 0;i < g[idx-1].size();i++) {
53 if(v1 <= g[idx-1][i].x1 && v2 >= g[idx-1][i].x2) {
54 }else if(v1 <= g[idx-1][i].x1 && v2 > g[idx-1][i].x1 && v2 <= g[idx-1][i].x2) {
55 g[idx].push_back(NODE(v2,g[idx-1][i].x2));
56 }else if(v1 >= g[idx-1][i].x1 && v1 < g[idx-1][i].x2 && v2 >= g[idx-1][i].x2) {
57 g[idx].push_back(NODE(g[idx-1][i].x1,v1));
58 }else if(v1 >= g[idx-1][i].x1 && v2 <= g[idx-1][i].x2) {
59 g[idx].push_back(NODE(g[idx-1][i].x1,v1));
60 g[idx].push_back(NODE(v2,g[idx-1][i].x2));
61 }else {
62 g[idx].push_back(g[idx-1][i]);
63 }
64 }
65 }
66
67
68 point_t cacu(point_t a,point_t b)
69 //b为ob,a为h
70 {
71 assert(h.y - root.y >= 0);
72 assert(h.y - ob.y >= 0);
73 return a + (b - a) * (h.y - root.y) / (h.y - ob.y);
74 }
75
76 int main()
77 {
78 int i,j,k;
79 while(scanf("%lf%lf%lf",&h.x1,&h.x2,&h.y) && (h.x1 || h.x2 || h.y)) {
80 scanf("%lf%lf%lf",&root.x1,&root.x2,&root.y);
81 scanf("%d",&n);
82 for(i = 0;i < N;i++) {
83 g[i].clear();
84 }
85 g[0].push_back(root);
86 for(i = 1,j = 0;i <= n;i++) {
87 scanf("%lf%lf%lf",&ob.x1,&ob.x2,&ob.y);
88 if(ob.y < h.y && ob.y > root.y) {
89 point_t v1 = cacu(point_t(h.x2,h.y) , point_t(ob.x1,ob.y));
90 point_t v2 = cacu(point_t(h.x1,h.y) , point_t(ob.x2,ob.y));
91 //printf("<%f,%f> <%f,%f>\n",v1.x,v1.y,v2.x,v2.y);
92 assert(v1.x <= v2.x && fabs(v1.y - v2.y) < eps);
93 cut(++j,v1.x,v2.x);
94 }
95 }
96 double res = 0;
97 for(i = 0;i < g[j].size();i++) {
98 res = max(res,g[j][i].x2 - g[j][i].x1);
99 }
100 if(res < eps) {
101 printf("No View\n");
102 }else {
103 printf("%.2f\n",res);
104 }
105 }
106 return 0;
107 }
108
109
1Y感觉很不错