Binary Stirling Numbers
| Time Limit: 1000MS |
|
Memory Limit: 10000K |
| Total Submissions: 1040 |
|
Accepted: 346 |
Description
The Stirling number of the second kind S(n, m) stands for the number of ways to partition a set of n things into m nonempty subsets. For example, there are seven ways to split a four-element set into two parts:
{1, 2, 3} U {4}, {1, 2, 4} U {3}, {1, 3, 4} U {2}, {2, 3, 4} U {1}
{1, 2} U {3, 4}, {1, 3} U {2, 4}, {1, 4} U {2, 3}.
There is a recurrence which allows to compute S(n, m) for all m and n.
S(0, 0) = 1; S(n, 0) = 0 for n > 0; S(0, m) = 0 for m > 0;
S(n, m) = m S(n - 1, m) + S(n - 1, m - 1), for n, m > 0.
Your task is much "easier". Given integers n and m satisfying 1 <= m <= n, compute the parity of S(n, m), i.e. S(n, m) mod 2.
Example
S(4, 2) mod 2 = 1.
Task
Write a program which for each data set:
reads two positive integers n and m,
computes S(n, m) mod 2,
writes the result.
Input
The first line of the input contains exactly one positive integer d equal to the number of data sets, 1 <= d <= 200. The data sets follow.
Line i + 1 contains the i-th data set - exactly two integers ni and mi separated by a single space, 1 <= mi <= ni <= 10^9.
Output
The output should consist of exactly d lines, one line for each data set. Line i, 1 <= i <= d, should contain 0 or 1, the value of S(ni, mi) mod 2.
Sample Input
1
4 2
Sample Output
1
Source
判断第二类斯特灵数模 2 的余数。
在刘汝佳的黑书上有详细解答，基本思路是枚举数值较小的斯特灵数，从中寻找规律。
下面这幅图是从维基百科截出来的，有一个二进制斯特灵数与组合数的转化公式。而组合数模二的余数就很容易了。
我们知道，组合数C（N,M）=N ! / M ! /(N-M)!,因而只需求得阶乘质因数分解式中二的重数即可解决问题。
而N ！质因数分解后2的重数可用下式来计算之。
K=N/2+N/2^2+N/2^3+....
上式的除法全是下取整。（可参见任何一本初等数论课本，如北大潘承洞编的那本《初等数论》）。
这样，这个问题就迎刃而解。
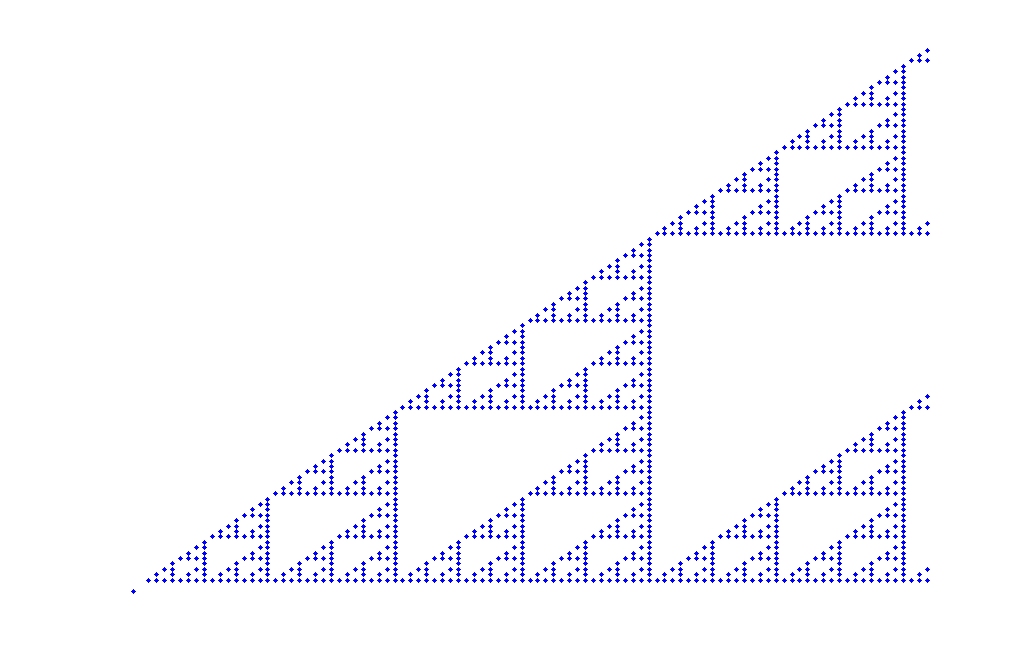
另外，有一点说明的是上面那个图形，就是分形几何中一个很重要的例子——谢彬斯基垫片。杨辉三角也有类似的形状。
这是我用MATLAB作的一个杨辉三角的二进制图形。
#include <stdio.h>
int main(int argc, char *argv[])
{
int n,m;
int z,w1,w2;
int t;
int a,b,c;
scanf("%d",&t);
while (t--)
{
scanf("%d%d",&n,&m);
z=n-(m+2)/2;
w1=(m-1)/2;
w2=z-w1;
a=0;
while (z)
{
z>>=1;
a+=z;
}
b=0;
while (w1)
{
w1>>=1;
b+=w1;
}
c=0;
while (w2)
{
w2>>=1;
c+=w2;
}
printf("%d\n",(a-b-c)==0);
}
return 0;
}