摘要: WA了N多次,猛然发现一处少写一符号,总算A掉了.这种题目就是要细心细心再细心.
#include <iostream>#include<cstring>#include<cmath>using namespace std;int main(){ char str[...
阅读全文
摘要: 两个都是麻烦的计数问题,只不过一个是二进制,另一个似乎更贴近十进制的现实世界.不过计算机里,还是二进制感觉能跑得更快一些,移位总比乘十来得更快一些.计数从0-n的每一位的数字个数,先计数位数小于n的位数的数字个数,再从高位到低位依次循环累加计数和n位数相同且小于n的数的各位数字.考虑的情形很多,有一点考虑不到就很难得到正确答案.
/**//*Source CodeProblem:&nb...
阅读全文
摘要: 给定有理数P/Q，求它的二进制小数的循环节长度。先把这个分数化为既约分数，则循环节开始的位置M是使满足2^M | Q的最大M。令Q1=Q/2^M,则循环节的长度就是求最小的N使2^N模Q1为1。这个问题好像没有有效的解法（关于Q1的位数为多项式级别）。由于2和Q1互素，可以用欧拉定理来解。即2^phi（Q1）对Q1同余1。所求的N一定是phi（Q1）的一个因子，先分解Q1，再分解phi（Q1），递...
阅读全文
http://acm.pku.edu.cn/JudgeOnline/problem?id=2085 给定整数N，和一个序列的逆序数M，求以1，2...N为元素，逆序为M，且按字典序最小的那个序列。
只要知道这样一个事实：一个序列的逆序唯一决定了这个序列。
例如：序列1，4，3，2的逆序为1--0，2--2，3--1，4--0，可以用一个四维坐标来表示（0，2，1，0），第i维的数是 i 在原序列中的逆序数，取值范围是0，1...4-i。
为解决这个问题，以N=4,逆序数M=5为例。
对这个问题可以采取贪心策略。
首先，如果所求序列以1为首，则1的逆序为0，可以从上表看出此时序列的逆序数最多为2+1=3<5，不满足。考虑以2为首，序列的逆序最多为3+1<5，不满足。
考虑以3为首，可见当1的逆序为3，2的逆序为2，4的逆序为0时满足要求，这时1，2，4均为最大逆序，因而只能排列为4，2，1，加上首数，所求序列为3，4，2，1。
若M=3，采取同样的贪心策略，可求得结果为1，4，3，2。
依此思路，可以得到所求序列关于N，M的关系式，具体如下：
1，2，3，...N-P, N-((p-1)*p/2-M), N , N-1...N-P+1.(P是满足（P-1）*P/2>=M的最小值)。
代码就容易多了。
关于更多排列的内容可参考：
/Files/sdz/s.doc
#include <stdio.h>
int main(int argc, char *argv[])
{
int n,m;
int p,temp,i;
while(scanf("%d%d",&n,&m) && n>0)
{
p=1;
while((p*(p-1))/2<m)p++;
temp=(p*(p-1))/2;
for(i=1;i<=n-p;i++)
printf("%d ",i);
printf("%d ",n-temp+m);
for(i=n;i>=n-p+1;i--)
{
if(i!=n-temp+m)
printf("%d ",i);
}
printf("\n");
}
return 0;
}
//Bridging signals 1631 最长上升子序列 dp问题 2010.8.13
#include <iostream>
using namespace std;
const int MAXP=40005;
int L[MAXP];
int bSearch(int left,int right,int num)
{
if(right==left)
return left;
int mid=(left+right)/2;
if(num==L[mid])
return mid;
else if(num>L[mid])
{
if(right<mid+1)
return mid;
else
return bSearch(mid+1,right,num);
}
else if(num<L[mid])
{
if(left>mid-1)
return mid;
else
return bSearch(left,mid,num);
}
else return mid;
}
int solve(int n)
{
int ans=0;
int temp=0;
int count=0;
scanf("%d",&temp);
L[ans++]=temp;
n--;
while(n--)
{
scanf("%d",&temp);
if(temp>L[ans-1])
L[ans++]=temp;
else
L[bSearch(0,ans-1,temp)]=temp;
}
return ans;
}
int main(int argc, char *argv[])
{
int t,n;
cin>>t;
while(t--)
{
cin>>n;
cout<<solve(n)<<endl;
}
return 0;
}
以前从没有对O（log N）和O（N）的区别有所正确认识，今日总算知道了。它们的唯一区别就是，N是一亿的时候，log(N)就是不到26，N还是一亿。
http://acm.pku.edu.cn/JudgeOnline/problem?id=3070
PKU的这道题虽然容易，但的确很有意思。我也是第一次用快速幂取模，一用，果然不同凡响。
快速幂取模，其实就是秦九韶算法 取指数。
把n化成二进制形式后，得到一个多项式,写成秦九韶形式，多项式的加就是乘，乘则为指数运算（指数为2）。由于N的二进制位个数为log(n),这样把O（N）的问题化为O（log N）。
.
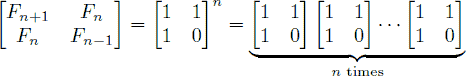//PKU 3070 ,calculate Fibonacci
#include <iostream>
#include<stack>
int FPM(int);//fast-power-modulus function declare
using namespace std;
const int Mod=10000;
int main(int argc, char *argv[])
{
int n=0;
while(scanf("%d",&n))
{
if(n==-1)
break;
printf("%d\n",FPM(n));
}
return 0;
}
int FPM(int n)//fast-power-modulus function
{
int matr[4]={1,0,0,1};//initialize matrix
stack<bool>dec;//stack to store binary digit
while(n)//resolve n to binary digit
{
dec.push(1&n);//get the last binary digit
n>>=1;
}
while(!dec.empty())
{
//matrix square
matr[1]=((matr[0]+matr[3])*matr[1])%Mod;
matr[0]=(matr[0]*matr[0]+matr[2]*matr[2])%Mod;
matr[3]=(matr[3]*matr[3]+matr[2]*matr[2])%Mod;
matr[2]=matr[1];
//matrix multiply,
if(dec.top())
{
matr[0]=(matr[0]+matr[1])%Mod;
matr[1]=(matr[1]+matr[3])%Mod;
matr[3]=matr[2];
matr[2]=matr[1];
}
dec.pop();
}
return matr[1];//matr[1] is the result F[N]
}