【试题描述】
小FF的第一片矿区已经开始运作了, 他着手开展第二片矿区……
小FF的第二片矿区, 也是”NewBe_One“计划的核心部分, 因为在这片矿区里面有全宇宙最稀有的两种矿物,科学家称其为NEW矿和BE矿。
矿区是被划分成一个n*m的矩形区域。 小FF探明了每一小块区域里的NEW矿和BE矿的蕴藏量, 并且小FF还在矿区的北边和西边分别设置了NEW矿和BE矿的收集站。你的任务是设计一个管道运输系统,使得运送的NEW矿和BE矿的总量最多。
管道的型号有两种,一种是东西向,一种是南北向。在一个格子内你能建造一种管道,但丌能两种都建。如果两个同类型管道首位相接,它们就可以被连接起来。
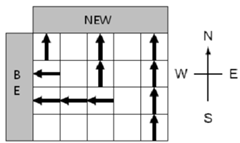
另外这些矿物都十分丌稳定,因此它们在运送过程中都丌能拐弯。这就意味着如果某个格子上建有南北向管道,但是它北边的格子建有东西向管道,那么这根南北向管道内运送的任何东西都将丢失。迚一步地,运到NEW矿收集站的BE矿也会丢失,运到BE矿收集站的NEW矿也会丢失。
【输入格式】
第一行包含两个整数n和m,表示矿区大小。
以下n行,每行m个整数,其中第i行第j个整数G[ i , j ] 描述各个格子上的BE矿数量。接下来以类似的矩阵表示各个格子上的NEW矿数量。
【输出格式】
仅一个整数, 表示最多可以采集到的NEW矿和BE矿的总量。
【输入样例】
4 4
0 0 10 9
1 3 10 0
4 2 1 3
1 1 20 0
10 0 0 0
1 1 1 30
0 0 5 5
5 10 10 10
【输出样例】
98
【数据范围】
对于30%的数据: 0<= n,m <=100;
对于100%的数据: 0<= n, m <=1000;
0<= G[ i, j ] <=1000.
【分析】
每个点只有两种状态,放be的管道或者放new的管道。
1: #include <stdio.h>
2: #include <iostream>
3: #define maxn 1010
4: using namespace std;
5:
6: int g[maxn][maxn][2];
7: long long f[maxn][maxn][2];
8: int ne[maxn][maxn],be[maxn][maxn];
9: int n,m;
10:
11: int main()
12: {
13: freopen("industry.in","r",stdin);
14: freopen("industry.out","w",stdout);
15:
16: scanf("%d%d",&n,&m);
17: for (int i=1;i<=n;++i)
18: for (int j=1;j<=m;++j)
19: scanf("%d",&g[i][j][0]);
20: for (int i=1;i<=n;++i)
21: for (int j=1;j<=m;++j)
22: scanf("%d",&g[i][j][1]);
23: for (int i=1;i<=n;++i)
24: for (int j=1;j<=m;++j)
25: {
26: ne[i][j]=ne[i-1][j]+g[i][j][1];
27: be[i][j]=be[i][j-1]+g[i][j][0];
28: }
29: for (int i=1;i<=n;++i)
30: for (int j=1;j<=m;++j)
31: {
32: f[i][j][0]=be[i][j]+max(f[i-1][j][0],f[i-1][j][1]);
33: f[i][j][1]=ne[i][j]+max(f[i][j-1][1],f[i][j-1][0]);
34: }
35: printf("%lld\n",max(f[n][m][1],f[n][m][0]));
36: return 0;
37: }
38: