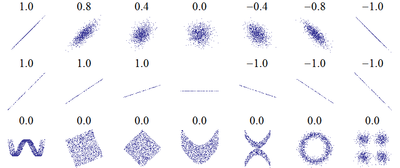
Several sets of (x, y) points, with the correlation coefficient of x and y for each set. Note that the correlation reflects the noisiness and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.
![\rho_{X,Y}=\mathrm{corr}(X,Y)={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E[(X-\mu_X)(Y-\mu_Y)] \over \sigma_X\sigma_Y},](http://upload.wikimedia.org/math/0/7/6/076d3820a46afe55ee680f3c85e34c76.png)
wiki上的一张图,很好的解释了相关与独立。。在相关系数为0的情况下,X Y分布很显然不独立。。
相关性系数是用来表征X Y之间线性关系紧密程度的量。当相关性系数为0 的时候,我们认为X Y不相关。
X Y独立 则X Y不相关,X Y不相关,则X Y不一定独立!
当时当X Y都满足高斯分布的时候,相关与独立可以互推。
上一次上课。。老师当堂提问二维高斯分布。。都忘了。。
![f(x,y) =
\frac{1}{2 \pi \sigma_x \sigma_y \sqrt{1-\rho^2}}
\exp\left(
-\frac{1}{2(1-\rho^2)}\left[
\frac{(x-\mu_x)^2}{\sigma_x^2} +
\frac{(y-\mu_y)^2}{\sigma_y^2} -
\frac{2\rho(x-\mu_x)(y-\mu_y)}{\sigma_x \sigma_y}
\right]
\right),](http://upload.wikimedia.org/math/b/1/0/b10ecc56f758b2f94a953e7e1bd2f1c2.png)
第一次发现wiki上的数学公式竟然有Latex源码。。Niubility!