1 随机化算法优点:
Best
Speed
Simplicity
Derandomization
Adversary argumetns and lower bounds
这个和没说一样。。
2 Randomized Algorithms 与average case analyasis的不同点。这个也是显然
3 快速排序的比较次数分析
<=n +2nln(n)
分析使用的技巧相当相当牛!
4 BSP问题:
Binary space partitioning (BSP) is a method for recursively subdividing a space into convex sets by hyperplanes. This subdivision gives rise to a representation of the scene by means of a tree data structure known as a BSP tree.
Originally, this approach was proposed in 3D computer graphics to increase the rendering efficiency. Some other applications include performing geometrical operations with shapes (constructive solid geometry) in CAD, collision detection in robotics and 3D computer games, and other computer applications that involve handling of complex spatial scenes.
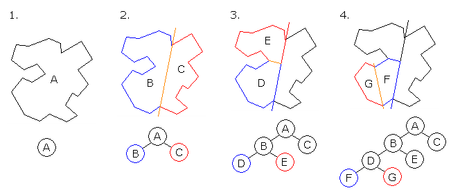
1. A is the root of the tree and the entire polygon
2. A is split into B and C
3. B is split into D and E.
4. D is split into F and G, which are convex and hence become leaves on the tree.
看一下这个图,不用介绍大概也明白了。。但是,我们需要多少次操作呢。。作者又进行了概率分析。。2*n *H(n) Harmonic Number还真是哪里都有。。服了。。
Other space partitioning structures其他的空间划分的数据结构
BSP trees divide a region of space into two subregions at each node. They are related to quadtrees and octrees, which divide each region into four or eight subregions, respectively.
Relationship Table
Name
p
s
Binary Space Partition
1
2
Quadtree
2
4
Octree
3
8
where p is the number of dividing planes used, and s is the number of subregions formed.
BSP trees can be used in spaces with any number of dimensions, but quadtrees and octrees are most useful in subdividing 2- and 3-dimensional spaces, respectively. Another kind of tree that behaves somewhat like a quadtree or octree, but is useful in any number of dimensions, is the kd-tree.
教程很新颖,虽然在北美开randomized Algorithms已经很多年了。。但是貌似在中国还没听说过这课程。。
利用概率分析的相当透彻。。把QuickSort和BSP数开始,进行了随机化过程中的比较次数的期望分析。。方法很新颖!
我用的这个讲义是UIUC 08的。。此外Berkerly 和CMU也有这门课程。。教材是那本尽人皆知的Randomized Algorithms。。。大牛啊!!