这个是算法导论习题5.2-4
n个顾客在进酒店之前,都会把自己的帽子给前台服务员保管。每个顾客在离开时,前台服务员又会随机地挑选一个帽子给他。问:最终,能拿到自己帽子的顾客们期望数是多少
首先从简单情况入手,对于n=2 n=3 很容易求出 结果res=1;
对于n>=4,我们严格的用概率方法来推导一下!
首先定义P(n)为伯努利放错信的问题的答案。
P_n=n!\sum_{i=2}^{n}\frac{(-1)^i}{i!}
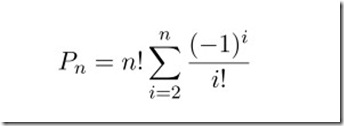
然后对于n个人中i个人匹配正确这个事件的数目是C(n,i)P(i)
总共有n!中事件,2^n种情况,(可以把人看成是10串,拿到自己帽子的为1)
所以 答案就是
(n-i)*C(n,i)P(i) /n!求和
整理一下是
\sum_{i=2}^{n-1}\frac{n-i}{(n-i)!}\sum_{j=2}^{i}\frac{(-1)^j}{j!}+\frac{1}{(n-1)!}
X2TC%604%7D(3J%5BXV_thumb.jpg)
可以证明这个等式等于1
所以答案是1