
考虑最后一位的循环...
#include<iostream>
using namespace std;
int main() {
long a,b;
int t,x[6],i;
while(cin>>a>>b){
x[1]=a=a%10;
i=1;
do {
++i;
x[i]=(x[i-1]*a)%10;
}while(x[i]!=x[1]);
t=i-1;
x[0]=x[i-1];
printf("%d\n",x[b%t]);
}
return 0;
}
最近周围很多人对字符串匹配算法比较感兴趣,特别是这次公司内部考试也可以认为是一个字符串查找的问题。
虽然字符串匹配看起来是个很简单、很成熟的问题,但在很多领域都有着很多的应用,比如模式匹配、特征提取等等。
这里对我知道的一些算法做些简单的整理,很不完善,有待改进~~~
1、 字符串匹配,即在字符串S中查找模式字符串P的出现
这个刚学过计算机的人也能写出代码,但事实上这个问题也可以子划分为若干特定问题域,比如,如果有单模式和多模式匹配问题(一个还是多个模式字符串,对于多个模式字符串的可以采用某些优化算法)
对于这类问题,最直接的想法就是在匹配时利用已获得的匹配信息尽可能多地跳过肯定不会匹配的部分,从而把复杂度从O(M*N)减少到线性复杂度。
教科书上的KMP(Knuth-Morris-Pratt)算是很成熟的一个利用这个思路的算法(作者之一就是Knuth大牛),最坏复杂度为O(M+N)(M和N分别为S和P的长度)
其他我知道的类似算法有BM(Boyer-Moore)算法(Snort系统中就用到了BM算法),最坏复杂度为O(M*N),最好复杂度为O(N/M),虽然看起来它的复杂度比KMP更高,但在实际应用中其效率比KMP更高,这也是为什么很多入侵检测系统优先选择BM的原因(理论复杂度和实际复杂度的差别还是很大的,比如最暴力的字符串匹配复杂度为O(M*N),也就是strstr的实现,可在实际应用中它的复杂度一般会退化到O(M+N))
另一个常见算法是WM算法,它的特点是适合于多模匹配问题。
很好的一个整理,大多数常见字符串算法集合:http://www-igm.univ-mlv.fr/~lecroq/string/index.html
WM算法的描述:http://hi.baidu.com/zcsong85/blog/item/8e3a22184c252b0335fa4156.html
2、 Suffix Tree
后缀树算是很常见的字符串数据结构之一了,它在模式匹配中的应用非常多,比如DNA序列检测等。
后缀树的基本思路是是对一个字符串的所有后缀子串以Tries的方式进行描述,从而可以迅速地在后缀树上找出字符串的任意子串。
所以对于已经建立了后缀树的字符串,做字符串查找已经算是非常简单的任务了,同时由于Tries的特点,这种结构可以很方便地处理前/后任意字符串匹配(比如“*ABC”和“ABC*”),为了要处理中间的wildcard,比如ABC*DEF,可以分别查找ABC*和*DEF,然后再取交集即可。
后缀树也很适合于多模匹配问题,但它适用的场景主要是待匹配字符串固定,而模式串未定的场景。
一个利用后缀树的典型应用是LCS(Longest Common Substring)最大公共子串问题。采用动态规划也可以很容易地解决LCS问题,但它的时空复杂度均为O(N*M),对于大多数应用是够了,可是,如果两个字符串是DNA序列,要从中间找出公共子串,O(N*M)的时空复杂度显然是无法接受的。而采用后缀树,复杂度就只是后缀树创建的复杂度,即O(N)
关于Suffix Tree的介绍可以参看:http://homepage.usask.ca/~ctl271/857/suffix_tree.shtml
3、 Aho-Corasick
Aho-Corasick自动机算法是一个非常高效的多模匹配算法,它的基本原理是对多个模式字符串构建有限状态机,而在源字符串中查找的过程则是一个状态机转换的过程。
它的最大缺点是构造状态机的复杂度较高,为O(KM^3)(K为模式串的个数,M为模式串的最大长度),但一旦构造后的查询效率则很高,为O(M*N)(N为源串长度)。
所以该算法很适用于多个模式字符串且模式字符串相对固定的使用场景(在Snort中也有使用),比如很多文本分类算法,需要在目标文本中查找活干特定关键字(features)出现频度,则可以使用A-C算法先对features建立状态机。
顺便说一下,linux下的fgrep也是利用A-C算法实现,虽然我也没想明白为什么需要?
http://en.wikipedia.org/wiki/Aho–Corasick_string_matching_algorithm
关于字符串还有很多其他有意思的话题,比如如何处理wildcard,如果进行regular expression的匹配,如何模糊匹配(在OCR中用到,Item被扫描成了ltem,如何纠正?),等等。
摘要: Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图
G=(V,E),其源点为s,加权函数
w是
边集 E
的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到
图G的任意顶点v的最短路径d[v]。
Bellman-For...
阅读全文
贪心,每次加入距离当前MST最近的一个点
//无向图最小生成树,prim算法,邻接阵形式,复杂度O(n^2)
//返回最小生成树的长度,传入图的大小n和邻接阵mat,不相邻点边权inf
//可更改边权的类型,pre[]返回树的构造,用父结点表示,根节点(第一个)pre值为-1
//必须保证图的连通的!
#define MAXN 200
#define inf 1000000000
typedef double elem_t;
elem_t prim(int n,elem_t mat[][MAXN],int* pre)
{
elem_t min[MAXN],ret=0;
int v[MAXN],i,j,k;
for (i=0;i<n;i++)
min[i]=inf,v[i]=0,pre[i]=-1;
for (min[j=0]=0;j<n;j++)
{
for (k=-1,i=0;i<n;i++)
if (!v[i]&&(k==-1||min[i]<min[k]))
k=i;
for (v[k]=1,ret+=min[k],i=0;i<n;i++)
if (!v[i]&&mat[k][i]<min[i])
min[i]=mat[pre[i]=k][i];
}
return ret;
}
贪心:
code:
//单源最短路径,dijkstra算法,邻接阵形式,复杂度O(n^2)
//求出源s到所有点的最短路经,传入图的顶点数n,(有向)邻接矩阵mat
//返回到各点最短距离min[]和路径pre[],pre[i]记录s到i路径上i的父结点,pre[s]=-1
//可更改路权类型,但必须非负!
#define MAXN 200
#define inf 1000000000
typedef int elem_t;
void dijkstra(int n,elem_t mat[][MAXN],int s,elem_t* min,int* pre)
{
int v[MAXN],i,j,k;
for (i=0;i<n;i++)
min[i]=inf,v[i]=0,pre[i]=-1;
for (min[s]=0,j=0;j<n;j++)
{
for (k=-1,i=0;i<n;i++)
if (!v[i]&&(k==-1||min[i]<min[k]))
k=i;
for (v[k]=1,i=0;i<n;i++)
if (!v[i]&&min[k]+mat[k][i]<min[i])
min[i]=min[k]+mat[pre[i]=k][i];
}
}
弗洛伊德(Floyd)算法过程:
1、用D[v][w]记录每一对顶点的最短距离。
2、依次扫描每一个点,并以其为基点再遍历所有每一对顶点D[][]的值,看看是否可用过该基点让这对顶点间的距离更小。
算法理解:
最短距离有三种情况:
1、两点的直达距离最短。(如下图<v,x>)
2、两点间只通过一个中间点而距离最短。(图<v,u>)
3、两点间用通过两各以上的顶点而距离最短。(图<v,w>)
对于第一种情况:在初始化的时候就已经找出来了且以后也不会更改到。
对于第二种情况:弗洛伊德算法的基本操作就是对于每一对顶点,遍历所有其它顶点,看看可否通过这一个顶点让这对顶点距离更短,也就是遍历了图中所有的三角形(算法中对同一个三角形扫描了九次,原则上只用扫描三次即可,但要加入判断,效率更低)。
对于第三种情况:如下图的五边形,可先找一点(比如x,使<v,u>=2),就变成了四边形问题,再找一点(比如y,使<u,w>=2),可变成三角形问题了(v,u,w),也就变成第二种情况了,由此对于n边形也可以一步步转化成四边形三角形问题。(这里面不用担心哪个点要先找哪个点要后找,因为找了任一个点都可以使其变成(n-1)边形的问题)。

floyd的核心代码:
for (k=0;k<g.vexnum;k++)
{
for (i=0;i<g.vexnum;i++)
{
for (j=0;j<g.vexnum;j++)
{
if (distance[i][j]>distance[i][k]+distance[k][j])
{
distance[i][j]=distance[i][k]+distance[k][j];
}
}
}
}
结合代码 并参照上图所示 我们来模拟执行下 这样才能加深理解:
第一关键步骤:当k执行到x,i=v,j=u时,计算出v到u的最短路径要通过x,此时v、u联通了。
第二关键步骤:当k执行到u,i=v,j=y,此时计算出v到y的最短路径的最短路径为v到u,再到y(此时v到u的最短路径上一步我们已经计算过来,直接利用上步结果)。
第三关键步骤:当k执行到y时,i=v,j=w,此时计算出最短路径为v到y(此时v到y的最短路径长在第二步我们已经计算出来了),再从y到w。
依次扫描每一点(k),并以该点作为中介点,计算出通过k点的其他任意两点(i,j)的最短距离,这就是floyd算法的精髓!同时也解释了为什么k点这个中介点要放在最外层循环的原因.
//多源最短路径,floyd_warshall算法,复杂度O(n^3)
//求出所有点对之间的最短路经,传入图的大小和邻接阵
//返回各点间最短距离min[]和路径pre[],pre[i][j]记录i到j最短路径上j的父结点
//可更改路权类型,路权必须非负!
#define MAXN 200
#define inf 1000000000
typedef int elem_t;
void floyd_warshall(int n,elem_t mat[][MAXN],elem_t min[][MAXN],int pre[][MAXN]){
int i,j,k;
for (i=0;i<n;i++)
for (j=0;j<n;j++)
min[i][j]=mat[i][j],pre[i][j]=(i==j)?-1:i;
for (k=0;k<n;k++)
for (i=0;i<n;i++)
for (j=0;j<n;j++)
if (min[i][k]+min[k][j]<min[i][j])
min[i][j]=min[i][k]+min[k][j],pre[i][j]=pre[k][j];
}
以上综述了各种排序方法的基本排序思想,使读者更进一步熟悉和掌握这些排序方法及排序过程。下面对这些排序方法从几个方面进行分析比较。
1.时间复杂度 ① 直接插入、直接选择、冒泡排序算法的时间复杂度为(n
2);
② 快速、归并、堆排序算法的时间复杂度为O(nlog
2n);
③ 希尔排序算法的时间复杂度很难计算,有几种较接近的答案:O(nlog
2n)或O(n
1.25);
④ 基数排序算法的时间复杂度为O(d*(rd+n)),其中rd是基数,d是关键字的位数,n是元素个数。
2.稳定性
① 直接插入、冒泡、归并和基数排序算法是稳定的;
② 直接选择、希尔、快速和堆排序算法是不稳定的。
3.辅助空间(空间复杂度)
① 直接插入、直接选择、冒泡、希尔和堆排序算法需要辅助空间为O(1);
② 快速排序算法需要辅助空间为O(lgn);
③ 归并排序算法需要辅助空间为O(n);
④ 基数排序算法需要辅助空间为O(n+rd)。
4.选取排序方法时需要考虑的主要因素有:
① 待排序的记录个数;
② 记录本身的大小和存储结构;
③ 关键字的分布情况;
④ 对排序稳定性的要求;
⑤ 时间和空间复杂度等。
5.排序方法的选取 ① 若待排序的一组记录数目n较小(如n≤50)时,可采用插入排序或选择排序。
② 若n较大时,则应采用快速排序、堆排序或归并排序。
③ 若待排序记录按关键字基本有序(正序或叫升序),则适宜选用直接插入排序、冒泡排序或快速排序。
④ 当n很大,而且关键字位数教少时,采用链式基数排序较好。
⑤ 关键字比较次数与记录的初始排列顺序无关的排序方法是选择排序。
6.排序方法对记录存储方式的要求:
① 当记录本身信息量较大时,插入排序、归并排序、基数排序易于在链表上实现;
② 快速排序、堆排序更适合用索引结构上排序;
一般的排序方法都是在顺序结构(一维数组)上实现。
v - w^2 + x^3 - y^4 + z^5 = target
tar str
1 ABCDEFGHIJKL
11700519 ZAYEXIWOVU
3072997 SOUGHT
1234567 THEQUICKFROG
0 END
找到 str中任意五个字符组合,使其满足v - w^2 + x^3 - y^4 + z^5 = target 的所有解中的字典序最大的那 V W X Y Z 的组合
简单DFS:
#include<iostream>
#include<string>
#include <algorithm>
#include <cstdlib>
using namespace std;
char ans[1000],str[20],res[20];
int t,len,mark[20],flag;
int cmp(const void *a,const void *b)
{
return *(char *)b-*(char *)a;
}
bool judge(int v,int w,int x,int y,int z)
{
if(v - w*w + x*x*x - y*y*y*y + z*z*z*z*z == t)
return true;
return false;
}
void DFS(int num)
{
if(flag)
return;
if(num == 5)
{
if (judge(res[0]-64,res[1]-64,res[2]-64,res[3]-64,res[4]-64))
{
strcpy(ans,res);
flag = 1;
}
return;
}
for(int i=0;i<len;i++)
{
if (!mark[i])
{
mark[i] = 1;
res[num] = str[i];
DFS(num+1);
mark[i] = 0;
}
}
}
int main()
{
int i,j,k;
while(scanf("%d %s",&t,str),strcmp(str,"END"))
{
len=strlen(str);flag=0;
qsort(str,len,sizeof(str[0]),cmp);
memset(mark,0,sizeof(mark));
DFS(0);
if(flag)
printf("%s\n",ans);
else
printf("no solution\n");
}
return 0;
}
1、整数划分问题是将一个正整数n拆成一组数连加并等于n的形式,且这组数中的最大加数不大于n。求划分的个数是基本要求:
//sprit()算法的作用求出它的个数,算法思想是:q(n,m)代表的是最大加数是m的划分的个数
/**
1、m==1||n==1 q(n,m)=1;
2、m>n q(n,m)=q(n,n)
3 m==n q(n,m)=q(n,m-1)+1;
4 m<n q(n,m)=q(n,m-1)+q(n-m,m)
**/
int sprit(int n,int m)
{
if(n==1||m==1)
return 1;
if(m>n)
return sprit(n,n);
if(m==n)
return sprit(n,m-1)+1;
if(m<n)
return sprit(n,m-1)+sprit(n-m,m);
return 0;
}
2、如果对时间复杂性要求高时,可以将其转换为非递归的形式,过程很简单
#define N 20
int ans[N][N];
void sprit_1()
{
int i,j;
for(i=1;i<N;i++)
for(j=1;j<=i;j++)
{
if(i==1||j==1)
ans[i][j]=1;
else if(i==j)
ans[i][j]=ans[i][j-1]+1;
else
{
int k=(i-j>=j?j:i-j);
ans[i][j]=ans[i][j-1]+ans[i-j][k];
}
}
}
3、/**将正整数划分成连续的正整数之和
如15可以划分成4种连续整数相加的形式:
15
7 8
4 5 6
1 2 3 4 5
划分思想是:设最小的数为x,划分个数为i,有x*i+i(i-1)/2=n,直接列举i即可
**/
void sprit_2(int n)
{
int i,j,t1,t2,x;
for(i=1;(t1=i*(i-1)/2)<n;i++)
{
t2=n-t1;
if(t2<0)return;
x=t2/i;
if((n-t1)%i==0)
{
for(j=0;j<i;j++)
cout<<x+j<<" ";
cout<<endl;
}
}
}
4、如果想把它的各种拆分也求出来,思想是用数组a保存结果,每次对指针t指向的数据进行拆分即可。
int a[N];
void f(int t)
{
int i,j,m;
for(i=0;i<=t;i++)
cout<<a[i]<<" ";
cout<<endl;
j=t;m=a[j];
for(i=a[j-1];i<=m/2;i++)
{
a[j]=i;a[j+1]=m-i;
f(j+1);
}
}
void sprit_3(int n)
{
for(int i=1;i<=n/2;i++)
{
a[0]=i;a[1]=n-i;
f(1);
}
}
本文将总结一种数据结构:跳跃表。前半部分跳跃表性质和操作的介绍直接摘自《让算法的效率跳起来--浅谈“跳跃表”的相关操作及其应用》上海市华东师范大学第二附属中学 魏冉。之后将附上跳跃表的源代码,以及本人对其的了解。难免有错误之处,希望指正,共同进步。谢谢。
跳跃表(Skip List)是1987年才诞生的一种崭新的数据结构,它在进行查找、插入、删除等操作时的期望时间复杂度均为O(logn),有着近乎替代平衡树的本领。而且最重要的一点,就是它的编程复杂度较同类的AVL树,红黑树等要低得多,这使得其无论是在理解还是在推广性上,都有着十分明显的优势。
首先,我们来看一下跳跃表的结构
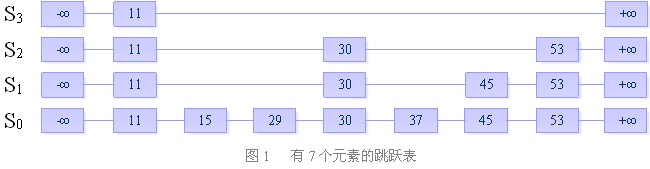
跳跃表由多条链构成(S0,S1,S2 ……,Sh),且满足如下三个条件:
每条链必须包含两个特殊元素:+∞ 和 -∞(其实不需要)
S0包含所有的元素,并且所有链中的元素按照升序排列。
每条链中的元素集合必须包含于序数较小的链的元素集合。
操作
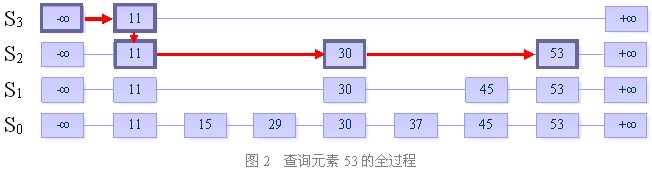
一、查找
目的:在跳跃表中查找一个元素x
在跳跃表中查找一个元素x,按照如下几个步骤进行:
1. 从最上层的链(Sh)的开头开始
2. 假设当前位置为p,它向右指向的节点为q(p与q不一定相邻),且q的值为y。将y与x作比较
(1) x=y 输出查询成功及相关信息
(2) x>y 从p向右移动到q的位置
(3) x<y 从p向下移动一格
3. 如果当前位置在最底层的链中(S0),且还要往下移动的话,则输出查询失败
二、插入
目的:向跳跃表中插入一个元素x
首先明确,向跳跃表中插入一个元素,相当于在表中插入一列从S0中某一位置出发向上的连续一段元素。有两个参数需要确定,即插入列的位置以及它的“高度”。
关于插入的位置,我们先利用跳跃表的查找功能,找到比x小的最大的数y。根据跳跃表中所有链均是递增序列的原则,x必然就插在y的后面。
而插入列的“高度”较前者来说显得更加重要,也更加难以确定。由于它的不确定性,使得不同的决策可能会导致截然不同的算法效率。为了使插入数据之后,保持该数据结构进行各种操作均为O(logn)复杂度的性质,我们引入随机化算法(Randomized Algorithms)。
我们定义一个随机决策模块,它的大致内容如下:
产生一个0到1的随机数r r ← random()
如果r小于一个常数p,则执行方案A, if r<p then do A
否则,执行方案B else do B
初始时列高为1。插入元素时,不停地执行随机决策模块。如果要求执行的是A操作,则将列的高度加1,并且继续反复执行随机决策模块。直到第i次,模块要求执行的是B操作,我们结束决策,并向跳跃表中插入一个高度为i的列。
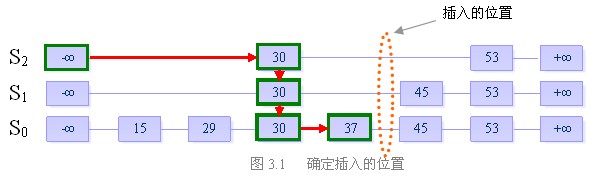
我们来看一个例子:
假设当前我们要插入元素“40”,且在执行了随机决策模块后得到高度为4
步骤一:找到表中比40小的最大的数,确定插入位置
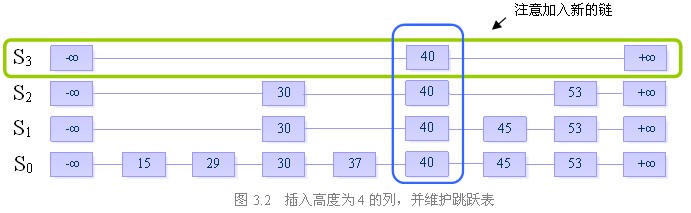
步骤二:插入高度为4的列,并维护跳跃表的结构
三、删除
目的:从跳跃表中删除一个元素x
删除操作分为以下三个步骤:
在跳跃表中查找到这个元素的位置,如果未找到,则退出
将该元素所在整列从表中删除
将多余的“空链”删除
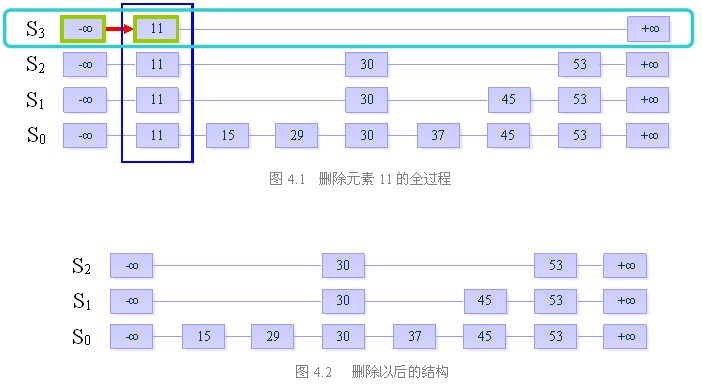
我们来看一下跳跃表的相关复杂度:
空间复杂度: O(n) (期望)
跳跃表高度: O(logn) (期望)
相关操作的时间复杂度:
查找: O(logn) (期望)
插入: O(logn) (期望)
删除: O(logn) (期望)
之所以在每一项后面都加一个“期望”,是因为跳跃表的复杂度分析是基于概率论的。有可能会产生最坏情况,不过这种概率极其微小。
--------------------------------------------------------------------------------
以下是自己学习时碰到的一些问题
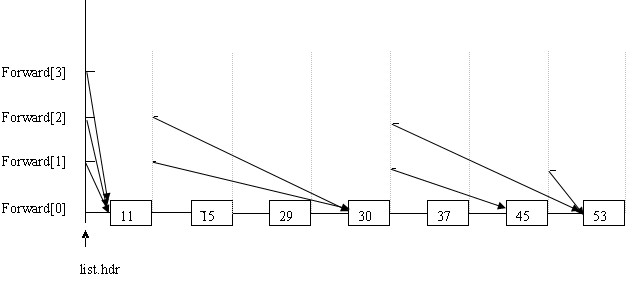
首先分配一个链表,用list.hdr指向,长度为跳跃表规定的最高层,说是链表,在以下代码中只是分配了一段连续的空间,用来指向每一层的开始位置。我们看到结构体nodeType中,有一个key,一个rec(用户数据),还有一个指向结构体的指针数组。
一开始的那些图容易给人误解。如上图所示,例如每个节点的forward[2],就认为是跳跃表的第3层。List.hdr的forward[2]指向11,11的forward[2]指向30,30的forward[2]指向53。这就是跳跃表的第3层:11---30-----53。(准确的说每个forward都指向新节点,新节点的同层forward又指向另一个节点,从而构成一个链表,而数据只有一个,并不是像开始途中所画的那样有N个副本)。本人天资愚钝,看了挺长时间才把它在内存里的结构看清楚了,呵呵。
以下是在网上搜到的一个实现代码
代码中主要注释了insert函数,剩下的两个函数差不多,就不一一注释了
/* skip list */
#include <stdio.h>
#include <stdlib.h>
/* implementation dependent declarations */
typedef enum {
STATUS_OK,
STATUS_MEM_EXHAUSTED,
STATUS_DUPLICATE_KEY,
STATUS_KEY_NOT_FOUND
} statusEnum;
typedef int keyType; /* type of key */
/* user data stored in tree */
typedef struct {
int stuff; /* optional related data */
} recType;
#define compLT(a,b) (a < b)
#define compEQ(a,b) (a == b)
/* levels range from (0 .. MAXLEVEL) */
#define MAXLEVEL 15
typedef struct nodeTag {
keyType key; /* key used for searching */
recType rec; /* user data */
struct nodeTag *forward[1]; /* skip list forward pointer */
} nodeType;
/* implementation independent declarations */
typedef struct {
nodeType *hdr; /* list Header */
int listLevel; /* current level of list */
} SkipList;
SkipList list; /* skip list information */
#define NIL list.hdr
static int count = 0;
statusEnum insert(keyType key, recType *rec) {
int i, newLevel;
nodeType *update[MAXLEVEL+1];
nodeType *x;
count++;
/***********************************************
* allocate node for data and insert in list *
***********************************************/
/* find where key belongs */
/*从高层一直向下寻找,直到这层指针为NIL,也就是说
后面没有数据了,到头了,并且这个值不再小于要插入的值。
记录这个位置,留着向其后面插入数据*/
x = list.hdr;
for (i = list.listLevel; i >= 0; i--) {
while (x->forward[i] != NIL
&& compLT(x->forward[i]->key, key))
x = x->forward[i];
update[i] = x;
}
/*现在让X指向第0层的X的后一个节点*/
x = x->forward[0];
/*如果相等就不用插入了*/
if (x != NIL && compEQ(x->key, key))
return STATUS_DUPLICATE_KEY;
/*随机的计算要插入的值的最高level*/
for (
newLevel = 0;
rand() < RAND_MAX/2 && newLevel < MAXLEVEL;
newLevel++);
/*如果大于当前的level,则更新update数组并更新当前level*/
if (newLevel > list.listLevel) {
for (i = list.listLevel + 1; i <= newLevel; i++)
update[i] = NIL;
list.listLevel = newLevel;
}
/* 给新节点分配空间,分配newLevel个指针,则这个
节点的高度就固定了,只有newLevel。更高的层次将
不会再有这个值*/
if ((x = malloc(sizeof(nodeType) + newLevel*sizeof(nodeType *))) == 0)
return STATUS_MEM_EXHAUSTED;
x->key = key;
x->rec = *rec;
/* 给每层都加上这个值,相当于往链表中插入一个数*/
for (i = 0; i <= newLevel; i++) {
x->forward[i] = update[i]->forward[i];
update[i]->forward[i] = x;
}
return STATUS_OK;
}
statusEnum delete(keyType key) {
int i;
nodeType *update[MAXLEVEL+1], *x;
/*******************************************
* delete node containing data from list *
*******************************************/
/* find where data belongs */
x = list.hdr;
for (i = list.listLevel; i >= 0; i--) {
while (x->forward[i] != NIL
&& compLT(x->forward[i]->key, key))
x = x->forward[i];
update[i] = x;
}
x = x->forward[0];
if (x == NIL || !compEQ(x->key, key)) return STATUS_KEY_NOT_FOUND;
/* adjust forward pointers */
for (i = 0; i <= list.listLevel; i++) {
if (update[i]->forward[i] != x) break;
update[i]->forward[i] = x->forward[i];
}
free (x);
/* adjust header level */
while ((list.listLevel > 0)
&& (list.hdr->forward[list.listLevel] == NIL))
list.listLevel--;
return STATUS_OK;
}
statusEnum find(keyType key, recType *rec) {
int i;
nodeType *x = list.hdr;
/*******************************
* find node containing data *
*******************************/
for (i = list.listLevel; i >= 0; i--) {
while (x->forward[i] != NIL
&& compLT(x->forward[i]->key, key))
x = x->forward[i];
}
x = x->forward[0];
if (x != NIL && compEQ(x->key, key)) {
*rec = x->rec;
return STATUS_OK;
}
return STATUS_KEY_NOT_FOUND;
}
void initList() {
int i;
/**************************
* initialize skip list *
**************************/
if ((list.hdr = malloc(
sizeof(nodeType) + MAXLEVEL*sizeof(nodeType *))) == 0) {
printf ("insufficient memory (initList)\n");
exit(1);
}
for (i = 0; i <= MAXLEVEL; i++)
list.hdr->forward[i] = NIL;
list.listLevel = 0;
}
int main(int argc, char **argv) {
int i, maxnum, random;
recType *rec;
keyType *key;
statusEnum status;
/* command-line:
*
* skl maxnum [random]
*
* skl 2000
* process 2000 sequential records
* skl 4000 r
* process 4000 random records
*
*/
maxnum = 20;
random = argc > 2;
initList();
if ((rec = malloc(maxnum * sizeof(recType))) == 0) {
fprintf (stderr, "insufficient memory (rec)\n");
exit(1);
}
if ((key = malloc(maxnum * sizeof(keyType))) == 0) {
fprintf (stderr, "insufficient memory (key)\n");
exit(1);
}
if (random) {
/* fill "a" with unique random numbers */
for (i = 0; i < maxnum; i++) key[i] = rand();
printf ("ran, %d items\n", maxnum);
} else {
for (i = 0; i < maxnum; i++) key[i] = i;
printf ("seq, %d items\n", maxnum);
}
for (i = 0; i < maxnum; i++) {
status = insert(key[i], &rec[i]);
if (status) printf("pt1: error = %d\n", status);
}
for (i = maxnum-1; i >= 0; i--) {
status = find(key[i], &rec[i]);
if (status) printf("pt2: error = %d\n", status);
}
for (i = maxnum-1; i >= 0; i--) {
status = delete(key[i]);
if (status) printf("pt3: error = %d\n", status);
}
return 0;
}