三、有穷状态自动机
人阅读正则表达式会比较简单,但是机器阅读正则表达式就是一件非常困难的事情了。而且,直接使用正则表达式进行匹配配的话,不仅工作量大,而且速度缓慢。因此我们还需要另外一种专门为机器设计的表达方式。本文在以后的章节中会给出一种算法把正则表达式转换为机器可以阅读的形式,就是这一章节所描述的有穷状态自动机。
有穷状态自动机这个名字听起来比较可怕,不过实际上这种自动机并没有想象中的那么复杂。状态机的这种概念被广泛的应用在各种各样的领域中。软件工程的统一建模语言(UML)有状态图,数字逻辑中也有状态转移图。不过这些各种各样的图在本质上都跟状态机没有什么区别。我将会通过一个例子来讲述状态的实际意义。
假设我们现在需要检查一个字符串中a的数量和b的数量是否都是偶数。当然我们可以用一个正则表达式来描述它。不过对于这个问题来说,用正则表达式来描述远远不如构造状态机方便。我们可以设计出一个状态的集合,然后指定集合中的某一个元素为“起始状态”。其实状态就是在工作还没开始的时候,分析器所处的状态。分析器在每一次进行一项新的工作的时候,都要把状态重置为起始状态。分析器每读入一个字符就修改一次状态,修改的方法我们也可以指定。分析器在读完所有的字符以后,必然停留在一个确定的状态中。如果这个状态跟我们所期望的状态一致的话,我们就说这个分析器接受了这个字符串,否则我们就说这个分析器拒绝了这个字符串。
如何通过设计状态及其转移方法来实现一个分析器呢?当然,如果一个字符串仅仅包含a或者b的话,那么分析器的状态只有四种:“奇数a奇数b”、“奇数a偶数b”、“偶数a奇数b”、“偶数a偶数 b”。我们把这些状态依次命名为aa、aB、Ab、AB。大写代表偶数,小写代表奇数。当工作还没开始的时候,分析器已经读入的字符串是空串,那么理所当然的起始状态应当是AB。当分析器读完所有字符的时候,我们期望读入的字符串的a和b的数量都是偶数,那么结束的状态也应该是AB。于是我们给出这样的一个状态图:
图3.1
检查一个字符串是否由偶数个a和偶数个b组成的状态图
在这个状态图里,有一个短小的箭头指向了AB,代表AB这个状态是初始状态。AB状态有粗的边缘,代表AB这个状态是结束的可接受状态。一个状态图的结束状态可以是一个或者多个。在这个例子里,起始状态和结束状态刚好是同一个状态。标有字符”a”的箭头从AB指向aB,代表如果分析器处于状态AB并且读入的字符是a的话,就转移到状态aB上。
我们把这个状态图应用在两个字符串上,分别是”abaabbba”和”aababbaba”。其中,第一个字符串是可以接受的,第二个字符串是不可接受的(因为有5个a和4个b)。
分析第一个字符串的时候,状态机所经过的状态是:
AB[a]aB[b]ab[a]Ab[a]ab[b]aB[b]ab[b]aB[a]AB
分析第二个字符串的时候,状态机所经过的状态是:
AB[a]aB[a]AB[b]Ab[a]ab[b]aB[b]ab[a]Ab[b]AB[a]aB
第一个字符串”abaabbba”让状态机在状态AB上停了下来,于是这个字符串是可以接受的。第二个字符串”aababbaba”让状态机在状态aB上停了下来,于是这个字符串是不可以接受的。
在机器内部表示这个状态图的话,我们可以使用一种比较简单的方法。这种方法仅仅把状态与状态之间的箭头、起始状态和结束状态集合记录下来。对应于这个状态图的话,我们就可以把这个状态图表示成以下形式:
起始状态:AB
结束状态集合:AB
(AB,a,aB)
(AB,b,Ab)
(aB,a,AB)
(aB,b,ab)
(Ab,a,ab)
(Ab,b,AB)
(ab,a,Ab)
(ab,b,aB)
用一个状态图来表示状态机的时候有时候会遇到确定性与非确定性的问题。所谓的确定性就是指对于任何一个状态,输入一个字符都可以跳转到另一个确定的状态中去。确定性和非确定性的区别有一个直观的描述:状态图的任何一个状态都可以有不定数量的边指向另一个状态,如果在这些边里面,存在两条边,它们所承载的字符如果相同,那么这个状态输入这个就字符可以跳转到另外两个状态中去,于是该状态机就是不确定的。如图所示:
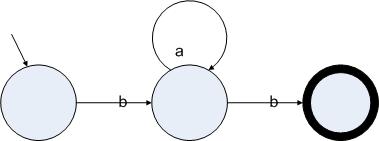
图3.2
正则表达式ba*b的一个确定的状态机表示
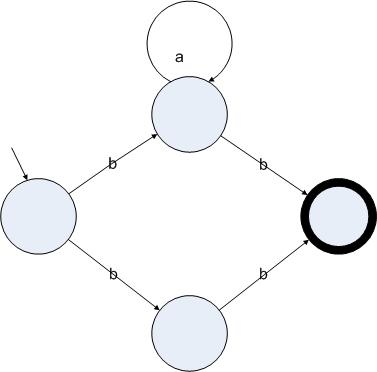
图3.3
正则表达式ba*b的一个非确定的状态机表示
图3.3中的状态机的起始状态读入字符b后可以跳转到中间的两个状态里,因此这个状态机是非确定的。相反,图3.2中的状态机,虽然功能跟图3.3的状态机一致,但却是确定的。我们还可以使用一种特殊的边来进行状态的转换。我们用ε边来表示一个状态可以不读入字符就跳转到另一个状态上。下图给出了一个跟图3.3功能一致的包含ε边的非确定的状态机:
图3.4
正则表达式ba*b的一个带有ε边的非确定的状态机
在教科书中,通常把确定的有穷状态自动机(有穷状态自动机也就是本文讨论的这种状态机)称为DFA,把非确定的有穷状态自动机称为NFA,把带有ε边的非确定的状态机称为ε-NFA。下文中也将采用这几个术语来指示各种类型的有穷状态自动机。
在刚刚接触到ε边的时候,一个通常的疑问就是这种边存在的理由。事实上如果是人直接画状态机的话,有时候也可以直接画出一个确定的状态机,复杂一点的话也可以画出一个非确定的状态机,在有些极端的情况下我们需要使用ε边来更加简洁的表示我们的意图。不过ε边存在的最大的理由就是:我们可以通过使用ε边来给出一个简洁的算法把一个正则表达式转换成ε-NFA。