最近在看波利亚的《数学与猜想》,关于普遍性和一般性是归纳的一种很有效的方法,就从一道题目开始吧。 证明直角三角形的三边a,b,c,其中a是斜边,满足a^2 = b^2 + c^2。 - 关于勾股定理,《Proofs Without Words》这本书里一开始就给我们提供了很多经典的图形证明。
- 这里为我们提供了很好的归纳法证明,形象的运用了一般性-特殊性的性质。
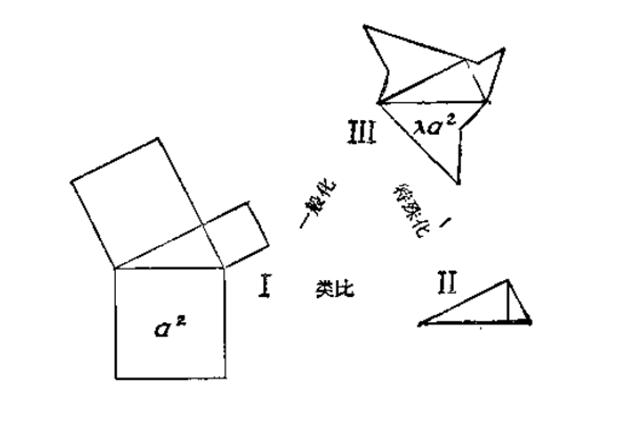
- 从I一般化到II,然后特殊化III。假如有三个相似多边形画在一个直角三角形的三边上,那么画在斜边上的多边形的面积应等于画在另外两边上的多边形面积之和。
接下来是另外一道题目。 一个三角形的三边长分别是l,m和n,其中它们都是正整数并且l<=m<=n[取n=1、2、3…],对于给定的n,求满足所述条件的不同三角形的个数,求出三角形的个数依赖于n的一般规律。 - 从n=1开始我们现列举一下
- n=1, 1 =1(m,l= 1,1)
- n=2, 2 =1+1(m,l= 2,2||2,1)
- n=3, 4 =3+1(m,l= 3,3||3,2||3,1||2,2)
或许你已经看出来了要满足条件的三角形首先要满足m>n/2,然后m+l>n,或许你已经想根据这些条件来进行概括了,但这个概括的过程未免太容易出错,我们不妨再列举下去。 - n=1, 1=1 (m,l= 1,1)
- n=2, 2=1+1 (m,l= 2,2||2,1)
- n=3, 4=3+1 (m,l= 3,3||3,2||3,1||2,2)
- n=4, 6=4+2 (m,l=4,4||4,3||4,2||4,1||3,3||3,2)
- n=5, 9=5+3+1 (m,l=5,5||5,4||5,3||5,2||5,1||4,4||4,3||4,2||3,3)
- ……
我想你应经看到规律了,他已经变成了一个纯数字的问题,而三角形的个数为n+(n-2)+(n-4)……这样再归纳就很简单了。

|