最近在看波利亚的《数学与猜想》，关于普遍性和一般性是归纳的一种很有效的方法，就从一道题目开始吧。

证明直角三角形的三边a，b，c，其中a是斜边，满足a^2 = b^2 + c^2。

• 关于勾股定理，《Proofs Without Words》这本书里一开始就给我们提供了很多经典的图形证明。
• 这里为我们提供了很好的归纳法证明，形象的运用了一般性-特殊性的性质。

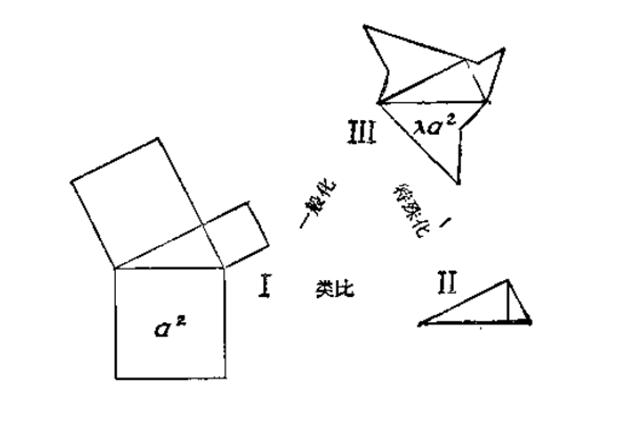
• 从I一般化到II，然后特殊化III。假如有三个相似多边形画在一个直角三角形的三边上，那么画在斜边上的多边形的面积应等于画在另外两边上的多边形面积之和。

接下来是另外一道题目。

一个三角形的三边长分别是l，m和n，其中它们都是正整数并且l<=m<=n[取n=1、2、3…]，对于给定的n，求满足所述条件的不同三角形的个数，求出三角形的个数依赖于n的一般规律。

• 从n=1开始我们现列举一下
• n=1, 1 =1(m,l= 1,1)
• n=2, 2 =1+1(m,l= 2,2||2,1)
• n=3, 4 =3+1(m,l= 3,3||3,2||3,1||2,2)

或许你已经看出来了要满足条件的三角形首先要满足m>n/2，然后m+l>n，或许你已经想根据这些条件来进行概括了，但这个概括的过程未免太容易出错，我们不妨再列举下去。

• n=1, 1=1 (m,l= 1,1)
• n=2, 2=1+1 (m,l= 2,2||2,1)
• n=3, 4=3+1 (m,l= 3,3||3,2||3,1||2,2)
• n=4, 6=4+2 (m,l=4,4||4,3||4,2||4,1||3,3||3,2)
• n=5, 9=5+3+1 (m,l=5,5||5,4||5,3||5,2||5,1||4,4||4,3||4,2||3,3)
• ……

我想你应经看到规律了，他已经变成了一个纯数字的问题，而三角形的个数为n+(n-2)+(n-4)……这样再归纳就很简单了。

前一段时间一直存在的问题，前几天才解决。MFC的程序在第一次相应菜单的时候屏幕会有闪烁问题。

当时就感觉比较怪，因为已经用了双缓冲，应该不存在这种问题。现在搞定了，感觉还是细节原理方面不是很了解。当然问题也有特殊性，就是菜单栏的事件响应是写在view里面的，但是只有第一次会有闪烁还是有些问题。

那么先要说一下MFC响应事件的过程：当点击一个菜单项的时候，最先接受到菜单项消息的是CMainFrame框架类，CMainFrame框架类将会把菜单项消息交给它的子窗口View类，由View类首先进行处理；如果View类检测到没对该菜单项消息做响应，则View类把菜单项消息交由文档类Doc类进行处理；如果Doc类检测到Doc类中也没对该菜单项消息做响应，则Doc类又把该菜单项消息交还给View类，由View类再交还给CMainFrame类处理。如果CMainFrame类查看到CMainFrame类中也没对该消息做响应，则最终交给App类进行处理。

看来问题是出现在活动view的选择上，因为一开始并没有指定活动的view，所以处理要有一个传递的过程，这导致了屏幕的刷新。这里我使用了暴力解决法，在mainframe加载的时候指定了activeview，那么就不会出现闪烁了。

另外在后来分屏CSplitterWnd的时候也出现了类似的问题，可以使用函数CSplitterWnd::SetActivePane()解决。

1、一道C TRAPS上的习题，写一段程序使支持嵌套注释和不支持嵌套注释的两种编译器运行的结果不一样。
语句肯定是从嵌套注释的地方来构造，两种编译器不同的地方就在于符号的匹配。
/* /* */ " */ " /* " /* */或者/* /* / 0* / **/1都可以，可以说是构造一个二义性的文法。

2、第二题是一道笔试题，写个函数pp(a,b),(其中a<b)打印出如下结果：
a
a+1
...
b-1
b
b-1
...
a+1
a
比如pp(1, 5)
1
2
3
4
5
4
3
2
1
。
题目就是这样，写出一个这样的函数应该不难，但题目要求是只使用一条语句，这就无疑增加了难度，
那我们分析如何才能用一条语句来构造呢？首先按照题目的输出来看肯定有循环，那我们先简单些，不用循环语句来写，递归式很好的形式，
它为我们提供了一种转换的很好形式，因为没有用到while等循环形式，只有条件判断的话还是很好处理的可以使用?:或者&&和||的运算规则
把第一个&&运算符改成，运算符也是可以的。

3、How to solve it的一道题目，用数字0~9构造一组数，使它们的和等于100,其中每个数字有且只能出现一次。
答案是没有这一组数的，可以证明如下：
这些数最大肯定不会超过两位，那么假设十位数字之和为t
则应满足10t + (45-t) =100
结果是不存在这个整数。
证明过程巧妙地转换了问题性质，并用方程的形式表示了出来。

OpenGL的位图和字体，两个函数glRasterPos*()和glBitmap()。
¤先说前一个，功能就是定位了下个位图的屏幕位置，但这里要注意屏幕位置是光栅位置，那么光栅位置又是什么位置呢，它并不是我们平时所使用的屏幕坐标，它要经过转换才能变成屏幕的坐标，就像画点的glVertex一样，反正坐标要经过模型矩阵和投影矩阵的变换来弄，具体就不说了。
然后要说到另一个兄弟，glWindowsPos* ()，它的目的是一样的，但是参数的坐标直接是屏幕坐标，不需要转换了，这对处理平面图像要更方便点，但绘制3D的话效果就不太好了。
这里面还有关于位图颜色的设置，注意颜色是在glRasterpos的时候确定的，在glRasterpos之后设置的颜色参数并不会改变位图的颜色。
¤然后是下个函数glBitmap()，这个函数参数比较多，各个的作用就不详细说了，每本教程上都有说明。但这里有个位图的width、height和glBitmap里的width、height之间的关系，在处理这个问题时，记住glBitmap的长宽高于一切，一切在它之外的数据都是废数据，可以舍弃不要了。

在看密码学的书时遇到的问题，求阶为p的有限域的乘法逆元。
GF(p)的概念就不讲了。乘法逆元么可以这样说，a关于m的乘法逆元就是使等式：a·b = 1 (mod m) ，成立的b。
开始我想要么就强搜，也用不了一次遍历。后来看了书上更简单的方法，运用的是辗转相除的思想，巧妙的进行方程的转化，过程是这样的。

1(A1, A2, A3) <- (1, 0, M); (B1, B2, B3)<-(0, 1, B)
2if B3 = 0 return A3 = gcd(m, b); no inverse
3if B3 = 1 return B3 = gcd(m, b); B2 = b` mod m
4Q = A3 / B3
5(T1, T2, T3) <- (A1-QB1, A2-QB2, A3-QB3)
6(A1, A2, A3) <- (B1, B2, B3)
7(B1, B2, B3) <- (T1, T2, T3)
8goto 2

其中A3和B3是gcd进行操作的主要参数。注意到求乘法逆元，那么m和b肯定互质。那么最后有gcd(m, b)=1，即B3=0，并且A3=1。因此在上一步有B3=1，那么：
mB1 + bB2 = B3
mB1 + bB2 =1
   bB2 = 1 - mB1
   bB2 = 1 (mod m)
所以此时的B2就为b的乘法逆元，全部过程利用辗转相除自然简化了不少。
推广一下可以求出b`，使bb` = k (mod m)，其中k为小余m的任意数。很简单，只要继续沿着此方法，算出bB2 = 1 (mod m)中的B2之后再乘以一个k (mod m)就是b`了。

一个人坐车回家究竟能干些什么呢？如果是短途车的话，恩应该蛮好打发的，在车上发发呆，做做白日梦还有听音乐，时间应该很快就过去了。如果做车的时间超过5个小时的话，我想还是会很无聊的，因为毕竟是一个人。那么你可以干些什么呢？最大众化的是一个人用时间来打发时间
可以：看书==不建议这种方式，因为有“四不要”，不知道你还记得不，有一条是不要在车上看书。
            听mp3==不错的方式，但是并不能依靠它来度过全部的时间。
            睡觉==嗯，这个最常见，车上到处是这样的家伙。
            把弄你的电子设备==这个是我们的最爱，从你的itouch到psp乃至你的手机、本本、相机。
            思考问题==这也是我比较喜欢的打发时间的方式，通常花些时间来想一些问题，闭上你的眼睛，集中你的注意力，不会损伤你的眼睛和耳朵，但不要走火入魔。
            和陌生人聊天==也很不错的方式，与人交流，很好很强大。
我想想也就这些了吧，以后想到了再补充。

下面记录一下今天回家路上的一些数字，嗯，真的是很无聊了。
0630 == 出发的时间了
20 == 貌似是出上海的公路交通费，囧……
100 == 车之前跑的路程长度km
200-5 == 高速公路的费用
5.4 == 现在的油价？（¥/L）
2 == 两张专辑
3 == 服务区
……
好了就这样吧。

 

这几天在重看C语言程序设计，嗯，感觉第一遍看的还是不够彻底。
貌似是练习2-1，叫你查看unsigned的范围。
当然可以在limit里面查看，但用程序来查看应也不难。
一开始我是这样想的，以unsigned char为例：

    unsigned char unch=1;
    unsigned char temp = 0;
    while(temp != unch)
    {
        temp = unch;
        unch = (unch << 1) + 1;
    }
    printf("%u", temp);

可以看出来，没问题。
后来想想不用这么麻烦，用~就行了。

    unsigned char temp = 0;
    temp = ~temp;
    printf("%u", temp);

一开始我是这样写的
直接在printf里面取反，结果并不是unsigned 的上限，变成了unsigned int的上限，看来是先自动进行了强制转换。

在深夜里用linux总不希望打扰到别人，系统的蜂鸣总会让人不自然。 rmmod pcspkr就可以了。 还有更好的办法，参见http://www.linuxidc.com/Linux/2009-04/19713.htm。 或者 在/etc/inputrc文件中把 set bell-style none 前的注释去掉,改为 set bell-style off。

C++博客在IE8下面要用兼容性视图才能写博客。嗯，很久没来博客里了，前一段时间有太多太多……就不说了。
回归主题，今天在zju上做了两题，因为刚开始，就已两个简单的开始。
1048&1049，很简单的两题。
但是有点要记录的，C++下面输出的格式化问题，以前用的是printf，cout不会用，今天学到了一点，格式化输出浮点数。
首先include头文件iomanip，浮点数限定小数点后的位数要用cout <<fixed<<showpoint然后cout<<setprecision(n)，其中n就是小数点后的位数。
cout还有其它的函数，见iomanip。
关于zju的1151题，我n久都没弄出来，但自己调试结果没问题，这种输出格式的问题最讨厌。

from:http://dev.csdn.net/develop/article/64/64485.shtm

; ======================================================================
;
;          Structure and Interpretation of Computer Programs
;                  (trial answer to excercises)
;
;                  计算机程序的构造和解释(习题试解)
;
;                                             created: code17 02/28/05
;                                             modified:
; (保持内容完整不变前提下，可以任意转载)
; ======================================================================

;; SICP No.1.25
;; 本题为理解题

;; 直接定义(expmod base exp m)为base^exp基于m的模(modulo)
;; (define (expmod base exp m)
;;   (remainder (fast-expt base exp) m))
;; 在理想情况下是正确的，在语义上与原定义是等价的，甚至递归层数
;; 都是一样的，而且更加直观。
;;
;; 但在实践中，这样的定义是不可行的，这也是为什么我们要采用原文中的定义
;; 的原因：因为base^exp很可能是一个非常大的数。比如，当我们取第二个
;; 测试例子中的n=1000000时，base是[1,999999]区间中的任意
;; 随机数，它的平均取值为50000，而exp=1000000。50000^1000000是一个大得
;; 惊人的数，无论是fast-expt的层层函数调用计算，还是用remainder对其取模，
;; 计算量都是很大的。
;;
;; 而相反，原始的expmod函数
;; (define (expmod base exp m)
;;   (cond ((= exp 0) 1)
;;         ((even? exp)
;;          (remainder (square (expmod base (/ exp 2) m))
;;                     m))
;;         (else
;;          (remainder (* base (expmod base (- exp 1) m))
;;                     m))))
;; 通过分解(a*b mod n) 为 ((a mod n) * (b mod n) mod n)，使得每层递归
;; 调用的计算参数和返回值总是小于n (x mod n < n)，即便是计算过程中出现
;; 的最大数(a mod n) * (b mod n) 也依然是要小于n^2, 相对于前者n^n的数
;; 量级，实在是小得多，这样就避免了大数的计算问题。
;;
;; 比如经测试，在使用新的expmod的情况下，1009的验证需要1.2ms的时间，
;; 1000003的验证需要 93680ms，远高于原来的expmod函数。
;;
;; 这也同时印证了我们在1.24题中的分析，同样的操作在不同字长的数字上的
;; 代价是不同的。1000000的验证时间现在是1000的8000多倍，远不再是2倍左右
;; 的关系。在1.24中的，因为expmod算法的控制，操作数最多是n^2级的，字长
;; 所引起的差距并不明显，只在10^6-10^12间产生了一点点阶跃；而这里的算法
;; 中, 操作数可以达到n^n级，当n=1000时，1000^1000的字长大约在10000位(二
;; 进制数)左右，而n=1000000时1000000^1000000的字长则达到在20000000位(二
;; 进制数)左右，这字长的巨大差距导致了我们在1.24中已经发现的问题更加明显。