思路:
这道题目的解法非常牛逼。刚一看题就知道做不出来了,所以就在这个博客
http://hi.baidu.com/findthegateopen/
找到了一份解题报告。下面的内容都是基于原作者的代码参考出来的。感谢原作者的代码!
朴素的做法是O(N^3)的复杂度。usaco官方的算法是O(N^2)的复杂度。原作者的代码跑了不到100ms,应该说是相当不错了!
首先,要把所有牛放到坐标系上来表示。目的,就是求出包含最多点的直角三角形。
直角三角形的两条直角边上都必须有点,也就是一组牛中的具有最小height的点和具有最小width的点。
直角三角形的边长也是固定的,cw = C/B,ch = C/A。这个还好说,从那个限制条件可以推出来的。初中都学过,呵呵。
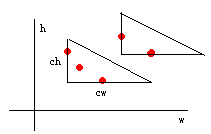
Step1:求出经过一个点的所有可能存在的三角形。
其实也就是在该点下方的灰色区域中选择点来确定一个三角形。
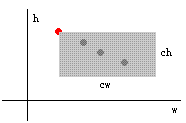
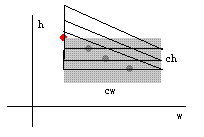
Step2:求出经过一个点的所有可能存在的三角形中,最多包含的点数。
解法相当精妙。
求一个三角形内的点数,可以分解为一个矩形内的点数减去一个梯形内的点数。
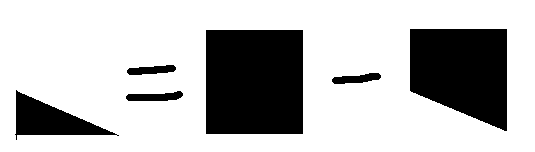
用这个方法,求出最上面那个三角形的点数之后。可以继续递推得到下面其他三角形的点数。
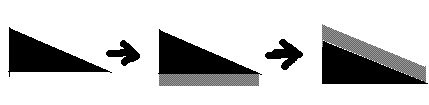
也就是加上一个矩形,再减去一个梯形。
如果点按照高度排序以后,那么后面矩形里的点一定是后出现的。这样就可以做到随时增加矩形。
但是减去梯形这个操作,就难理解一点,把点按照A*H + B*W来排序,就能保证后面梯形里的点一定是后出现的。
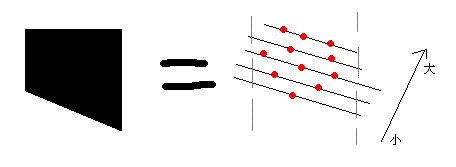
可见,A*H + B*W 值的大小决定了他们的位置分布。完全可以保证这个顺序。
这种数形结合的方法实在是相当精妙!
那我们就可以首先求出第一个三角形的点数,然后接下来的三角形就根据减去梯形,和增加矩形的操作,来做小的调整就可以了。
在代码里面的表现形式就是维护两个指针,不断向后移,中间剔除横坐标不在范围之内的点。
这个操作的复杂度是O(N)。
对所有点执行一次,故算法的复杂度是O(N^2)。
代码:

 /**//*
/**//*
 * 本代码参考自 http://hi.baidu.com/findthegateopen/
* 本代码参考自 http://hi.baidu.com/findthegateopen/
 * 中的代码,感谢原作者的代码!
* 中的代码,感谢原作者的代码!
 */
*/
 #include <stdio.h>
#include <stdio.h>
 #include <stdlib.h>
#include <stdlib.h>

 #define MAX_N 1024
#define MAX_N 1024


 struct node
struct node  {
{
 int w, h, k;
int w, h, k;
 };
};

 struct node in[MAX_N], *sort_h[MAX_N], *sort_k[MAX_N];
struct node in[MAX_N], *sort_h[MAX_N], *sort_k[MAX_N];
 int A, B, C, N, ch, cw, ans, box, slash, cnt;
int A, B, C, N, ch, cw, ans, box, slash, cnt;

 int cmp_h(const void *a, const void *b)
int cmp_h(const void *a, const void *b)


 {
{
 return (*(struct node **)b)->h - (*(struct node **)a)->h;
return (*(struct node **)b)->h - (*(struct node **)a)->h;
 }
}

 int cmp_k(const void *a, const void *b)
int cmp_k(const void *a, const void *b)


 {
{
 return (*(struct node **)b)->k - (*(struct node **)a)->k;
return (*(struct node **)b)->k - (*(struct node **)a)->k;
 }
}

 __inline void update(int h, int w)
__inline void update(int h, int w)


 {
{
 int k;
int k;

 for ( ; box < N && sort_h[box]->h >= h; box++)
for ( ; box < N && sort_h[box]->h >= h; box++)
 if (sort_h[box]->w >= w && sort_h[box]->w <= w + cw)
if (sort_h[box]->w >= w && sort_h[box]->w <= w + cw)
 cnt++;
cnt++;
 k = A * h + B * w + C;
k = A * h + B * w + C;
 for ( ; slash < N && sort_k[slash]->k > k; slash++)
for ( ; slash < N && sort_k[slash]->k > k; slash++)
 if (sort_k[slash]->w >= w && sort_k[slash]->w <= w + cw)
if (sort_k[slash]->w >= w && sort_k[slash]->w <= w + cw)
 cnt--;
cnt--;
 if (cnt > ans)
if (cnt > ans)
 ans = cnt;
ans = cnt;
 }
}

 __inline void calc(int i)
__inline void calc(int i)


 {
{
 int h, w;
int h, w;

 box = 0;
box = 0;
 slash = 0;
slash = 0;
 cnt = 0;
cnt = 0;
 h = sort_h[i]->h;
h = sort_h[i]->h;
 w = sort_h[i]->w;
w = sort_h[i]->w;
 for ( ; i < N && sort_h[i]->h >= h - ch; i++)
for ( ; i < N && sort_h[i]->h >= h - ch; i++)
 if (sort_h[i]->w >= w && sort_h[i]->w <= w + cw)
if (sort_h[i]->w >= w && sort_h[i]->w <= w + cw)
 update(sort_h[i]->h, w);
update(sort_h[i]->h, w);
 }
}

 int main()
int main()


 {
{
 int i;
int i;

 freopen("e:\\test\\in.txt", "r", stdin);
freopen("e:\\test\\in.txt", "r", stdin);

 scanf("%d%d%d%d", &N, &A, &B, &C);
scanf("%d%d%d%d", &N, &A, &B, &C);
 cw = C/B;
cw = C/B;
 ch = C/A;
ch = C/A;

 for (i = 0; i < N; i++)
for (i = 0; i < N; i++)  {
{
 scanf("%d%d", &in[i].h, &in[i].w);
scanf("%d%d", &in[i].h, &in[i].w);
 in[i].k = A * in[i].h + B * in[i].w;
in[i].k = A * in[i].h + B * in[i].w;
 sort_h[i] = &in[i];
sort_h[i] = &in[i];
 sort_k[i] = &in[i];
sort_k[i] = &in[i];
 }
}
 qsort(sort_h, N, sizeof(sort_h[0]), cmp_h);
qsort(sort_h, N, sizeof(sort_h[0]), cmp_h);
 qsort(sort_k, N, sizeof(sort_k[0]), cmp_k);
qsort(sort_k, N, sizeof(sort_k[0]), cmp_k);

 for (i = 0; i < N; i++)
for (i = 0; i < N; i++)
 calc(i);
calc(i);
 printf("%d\n", ans);
printf("%d\n", ans);

 return 0;
return 0;
 }
}

