|
|
朴素的Prim！
 #include <stdio.h>
int map[128][128], set[128], N, tm;
__inline int prim()
   {
 int sum, i, j, k, min_val, min_idx;
tm++;
set[0] = tm;
sum = 0;
  for (i = 0; i < N - 1; i++) {
min_val = 0x7fffffff;
for (j = 0; j < N; j++) {
if (set[j] != tm)
continue;
for (k = 0; k < N; k++) {
if (set[k] != tm && map[j][k] < min_val) {
min_val = map[j][k];
min_idx = k;
 }
}
}
sum += min_val;
set[min_idx] = tm;
}
return sum;
 }
int main()
{
int i, j;
freopen("e:\\test\\in.txt", "r", stdin);
while (scanf("%d", &N) != EOF) {
for (i = 0; i < N; i++)
for (j = 0; j < N; j++)
scanf("%d", &map[i][j]);
printf("%d\n", prim());
}
return 0;
}
用的SPFA算法。
#include <stdio.h>
#include <stdlib.h>
#define MAX_N 1024
#define MAX_T 2048
struct edge_node {
int idx, len;
struct edge_node *next;
};
struct edge_node edges[MAX_T * 2], *map[MAX_N];
int N, T, D[MAX_N], queue[MAX_N], qh, qt, visited[MAX_N];
__inline void add_edge(struct edge_node *e, int from, int to, int len)
{
e->idx = to;
e->len = len;
e->next = map[from];
map[from] = e;
}
int main()
{
int i, from, to, len;
struct edge_node *e;
freopen("e:\\test\\in.txt", "r", stdin);
scanf("%d%d", &T, &N);
for (i = 0; i < T * 2; i += 2) {
scanf("%d%d%d", &from, &to, &len);
add_edge(&edges[i], from, to, len);
add_edge(&edges[i + 1], to, from, len);
}
for (i = 1; i <= N; i++)
D[i] = 0x00ffffff;
queue[0] = N;
visited[N] = 1;
D[N] = 0;
qh = 0;
qt = 1;
while (qh != qt) {
i = queue[qh++];
qh &= _countof(queue) - 1;
visited[i] = 0;
for (e = map[i]; e; e = e->next) {
if (D[i] + e->len < D[e->idx]) {
D[e->idx] = D[i] + e->len;
if (!visited[e->idx]) {
visited[e->idx] = 1;
queue[qt++] = e->idx;
qt &= _countof(queue) - 1;
}
}
}
}
printf("%d\n", D[1]);
return 0;
}
注意：
要去掉前面的0再输出。
#include <stdio.h>
#include <string.h>
struct node {
char arr[128];
int len;
};
__inline int max(int a, int b)
{
return a > b ? a : b;
}
__inline void add(struct node *a, struct node *b)
{
int i, val;
for (val = i = 0; i < max(a->len, b->len); i++) {
if (i < a->len)
val += a->arr[i];
if (i < b->len)
val += b->arr[i];
a->arr[i] = val % 10;
val /= 10;
}
if (val)
a->arr[i++] = val;
a->len = i;
}
__inline void mul_single(struct node *a, int val, int pad, struct node *c)
{
int i, r;
for (i = 0; i < pad; i++)
c->arr[i] = 0;
c->len = pad;
for (r = i = 0; i < a->len; i++) {
r += a->arr[i] * val;
c->arr[c->len++] = r % 10;
r /= 10;
}
if (r)
c->arr[c->len++] = r;
}
__inline void mul(struct node *a, struct node *b, struct node *c)
{
struct node t;
int i;
c->len = 0;
for (i = 0; i < a->len; i++) {
mul_single(b, a->arr[i], i, &t);
add(c, &t);
}
}
__inline void input(struct node *t)
{
char str[sizeof(t->arr)];
int i, len;
scanf("%s", str);
len = strlen(str);
t->len = 0;
for (i = len - 1; i >= 0; i--)
t->arr[t->len++] = str[i] - '0';
}
__inline void output(struct node *t)
{
int i;
for (i = t->len - 1; i >= 0 && !t->arr[i]; i--);
if (i < 0) {
printf("0\n");
return ;
}
for ( ; i >= 0; i--)
putc(t->arr[i] + '0', stdout);
putc('\n', stdout);
}
int main()
{
struct node a, b, c;
freopen("e:\\test\\in.txt", "r", stdin);
input(&a);
input(&b);
mul(&a, &b, &c);
output(&c);
return 0;
}
纪念一下，跟我生日一样的题目。 思路： 这题可以用并查集来做，也是挺取巧的。 每个栈看做是一个集合，用一个数组记录栈中元素离栈底的距离，一个数组记录每个栈底元素对应的栈顶的元素。 对于移动操作，只需要合并集合，然后更改栈顶元素数组就行了。 用了栈写的路径压缩，代码跑到230ms。不知道那些100ms是怎么搞出来的。。真的有什么神奇技巧吗。
#include <stdio.h>
#define MAX_N 30032
int top[MAX_N];
struct set_node {
int parent, dis;
};
struct set_node set[MAX_N];
__inline int find(int idx)
{
static int stk[MAX_N], sp, i;
for (sp = 0; set[idx].parent; sp++) {
stk[sp] = idx;
idx = set[idx].parent;
}
for (sp--; sp >= 0; sp--) {
i = stk[sp];
set[i].dis += set[set[i].parent].dis;
set[i].parent = idx;
}
return idx;
}
int main()
{
int p, a, b;
char op[16];
freopen("e:\\test\\in.txt", "r", stdin);
for (a = 0; a < MAX_N; a++)
top[a] = a;
scanf("%d", &p);
while (p--) {
scanf("%s%d", op, &a);
if (op[0] == 'M') {
scanf("%d", &b);
a = find(a);
b = find(b);
set[a].parent = top[b];
set[a].dis = 1;
top[b] = top[a];
} else {
find(a);
printf("%d\n", set[a].dis);
}
}
return 0;
}
思路：
由于W的值 <= 30，比较小，所以这题可以用动态规划来做。
首先要把连续同一个数字一次处理。
dp[i] = {走了 i 次以后，得到的最大的苹果数目}。这个数组的大小为 W。
走了奇数次以后，一定位于树2下面。
走了偶数次以后，一定位于树1下面。
假设当前是在第 t 时刻掉了 cnt 个苹果下来。val 表示哪棵树掉的苹果，则执行下面的操作更新数组就可以了。
if (val == 1) {
for (i = 0; i <= min(t, W); i += 2)
dp[i] += cnt;
for (i = 1; i <= min(t, W); i += 2)
dp[i + 1] = max(dp[i + 1], dp[i] + cnt);
} else {
for (i = 1; i <= min(t, W); i += 2)
dp[i] += cnt;
for (i = 0; i <= min(t, W); i += 2)
dp[i + 1] = max(dp[i + 1], dp[i] + cnt);
}
转移方程就是这个，还是挺简单的。
因为数据弱，代码 0ms ac了。
完整代码：
#include <stdio.h>
int T, W, dp[35], t;
__inline int max(int a, int b)
{
return a > b ? a : b;
}
__inline int min(int a, int b)
{
return a < b ? a : b;
}
__inline void calc(int val, int cnt)
{
int i;
if (val == 1) {
for (i = 0; i <= min(t, W); i += 2)
dp[i] += cnt;
for (i = 1; i <= min(t, W); i += 2)
dp[i + 1] = max(dp[i + 1], dp[i] + cnt);
} else {
for (i = 1; i <= min(t, W); i += 2)
dp[i] += cnt;
for (i = 0; i <= min(t, W); i += 2)
dp[i + 1] = max(dp[i + 1], dp[i] + cnt);
}
t++;
}
int main()
{
int i, pre, cnt;
freopen("e:\\test\\in.txt", "r", stdin);
scanf("%d%d%d", &T, &W, &pre);
cnt = 1;
while (--T) {
scanf("%d", &i);
if (i == pre) {
cnt++;
continue;
}
calc(pre, cnt);
cnt = 1;
pre = i;
}
calc(pre, cnt);
cnt = 0;
for (i = 0; i <= W; i++)
cnt = max(cnt, dp[i]);
printf("%d\n", cnt);
return 0;
}
昨天做了2008，今天准备做2009。但是看了下题目，发现爆难，才100个人过。
觉得这种题还是别碰了，等以后牛逼了再做。
于是跳过2008年，直接到2010年了！呵呵。
这题还是算容易的，比较适合自己水平发挥，用堆来做，速度尚可 188ms 。
思路： 先把牛按照score排序一下，然后从后往前找，把每一头牛当做是位于中间的那头牛。 那现在就是求： 该头牛前面的所有牛中，哪 (N - 1) / 2 头牛aid值的和最小。 该头牛后面的所有牛中，哪 (N - 1) / 2 头牛aid值的和最小。 这就是典型的用堆可以解决的问题了。
#include <stdio.h>
#include <stdlib.h>
#define MAX_C 100032
#define MAX_N 20032
struct node {
int score, aid;
};
struct node in[MAX_C];
int N, C, F;
int after[MAX_C], before[MAX_C];
int heap_size, heap_sum, heap[MAX_N];
int cmp(const void *a, const void *b)
{
return ((struct node *)a)->score - ((struct node *)b)->score;
}
__inline void shift_down(int idx)
{
int val = heap[idx];
while (1) {
idx *= 2;
if (idx > heap_size)
break ;
if (idx + 1 <= heap_size && heap[idx + 1] > heap[idx])
idx++;
if (heap[idx] <= val)
break;
heap[idx / 2] = heap[idx];
}
heap[idx / 2] = val;
}
__inline int heap_init(int start, int len)
{
int i;
heap_sum = 0;
for (i = start; i < start + len; i++) {
heap[i - start + 1] = in[i].aid;
heap_sum += in[i].aid;
}
for (i = heap_size / 2; i >= 1; i--)
shift_down(i);
return heap_sum;
}
__inline int heap_update(int aid)
{
if (aid < heap[1]) {
heap_sum -= heap[1] - aid;
heap[1] = aid;
shift_down(1);
}
return heap_sum;
}
int main()
{
int i;
freopen("e:\\test\\in.txt", "r", stdin);
scanf("%d%d%d", &N, &C, &F);
for (i = 0; i < C; i++)
scanf("%d%d", &in[i].score, &in[i].aid);
qsort(in, C, sizeof(in[0]), cmp);
heap_size = (N - 1) / 2;
before[heap_size - 1] = heap_init(0, heap_size);
for (i = heap_size; i < C; i++)
before[i] = heap_update(in[i].aid);
after[C - heap_size] = heap_init(C - heap_size, heap_size);
for (i = C - heap_size - 1; i >= 0; i--)
after[i] = heap_update(in[i].aid);
for (i = C - heap_size - 1; i - heap_size >= 0; i--) {
if (in[i].aid + before[i - 1] + after[i + 1] <= F)
break;
}
printf("%d\n", i - heap_size < 0 ? -1 : in[i].score);
return 0;
}
思路：
这道题目的解法非常牛逼。刚一看题就知道做不出来了，所以就在这个博客
http://hi.baidu.com/findthegateopen/
找到了一份解题报告。下面的内容都是基于原作者的代码参考出来的。感谢原作者的代码！
朴素的做法是O(N^3)的复杂度。usaco官方的算法是O(N^2)的复杂度。原作者的代码跑了不到100ms，应该说是相当不错了！
首先，要把所有牛放到坐标系上来表示。目的，就是求出包含最多点的直角三角形。
直角三角形的两条直角边上都必须有点，也就是一组牛中的具有最小height的点和具有最小width的点。
直角三角形的边长也是固定的，cw = C/B，ch = C/A。这个还好说，从那个限制条件可以推出来的。初中都学过，呵呵。
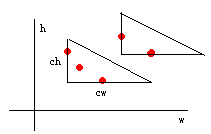
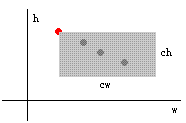
Step1：求出经过一个点的所有可能存在的三角形。
其实也就是在该点下方的灰色区域中选择点来确定一个三角形。
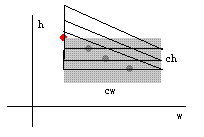  Step2：求出经过一个点的所有可能存在的三角形中，最多包含的点数。 解法相当精妙。 求一个三角形内的点数，可以分解为一个矩形内的点数减去一个梯形内的点数。 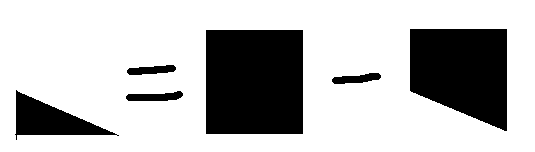 用这个方法，求出最上面那个三角形的点数之后。可以继续递推得到下面其他三角形的点数。 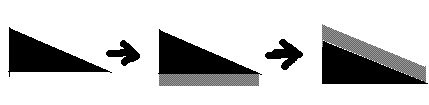 也就是加上一个矩形，再减去一个梯形。 如果点按照高度排序以后，那么后面矩形里的点一定是后出现的。这样就可以做到随时增加矩形。 但是减去梯形这个操作，就难理解一点，把点按照A*H + B*W来排序，就能保证后面梯形里的点一定是后出现的。 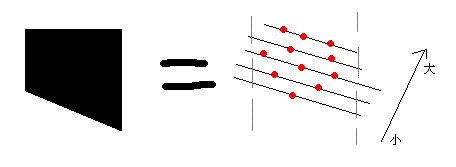 可见，A*H + B*W 值的大小决定了他们的位置分布。完全可以保证这个顺序。 这种数形结合的方法实在是相当精妙！ 那我们就可以首先求出第一个三角形的点数，然后接下来的三角形就根据减去梯形，和增加矩形的操作，来做小的调整就可以了。 在代码里面的表现形式就是维护两个指针，不断向后移，中间剔除横坐标不在范围之内的点。 这个操作的复杂度是O(N)。 对所有点执行一次，故算法的复杂度是O(N^2)。 代码：
/**//*
* 本代码参考自 http://hi.baidu.com/findthegateopen/
* 中的代码，感谢原作者的代码！
*/
#include <stdio.h>
#include <stdlib.h>
#define MAX_N 1024
struct node {
int w, h, k;
};
struct node in[MAX_N], *sort_h[MAX_N], *sort_k[MAX_N];
int A, B, C, N, ch, cw, ans, box, slash, cnt;
int cmp_h(const void *a, const void *b)
{
return (*(struct node **)b)->h - (*(struct node **)a)->h;
}
int cmp_k(const void *a, const void *b)
{
return (*(struct node **)b)->k - (*(struct node **)a)->k;
}
__inline void update(int h, int w)
{
int k;
for ( ; box < N && sort_h[box]->h >= h; box++)
if (sort_h[box]->w >= w && sort_h[box]->w <= w + cw)
cnt++;
k = A * h + B * w + C;
for ( ; slash < N && sort_k[slash]->k > k; slash++)
if (sort_k[slash]->w >= w && sort_k[slash]->w <= w + cw)
cnt--;
if (cnt > ans)
ans = cnt;
}
__inline void calc(int i)
{
int h, w;
box = 0;
slash = 0;
cnt = 0;
h = sort_h[i]->h;
w = sort_h[i]->w;
for ( ; i < N && sort_h[i]->h >= h - ch; i++)
if (sort_h[i]->w >= w && sort_h[i]->w <= w + cw)
update(sort_h[i]->h, w);
}
int main()
{
int i;
freopen("e:\\test\\in.txt", "r", stdin);
scanf("%d%d%d%d", &N, &A, &B, &C);
cw = C/B;
ch = C/A;
for (i = 0; i < N; i++) {
scanf("%d%d", &in[i].h, &in[i].w);
in[i].k = A * in[i].h + B * in[i].w;
sort_h[i] = &in[i];
sort_k[i] = &in[i];
}
qsort(sort_h, N, sizeof(sort_h[0]), cmp_h);
qsort(sort_k, N, sizeof(sort_k[0]), cmp_k);
for (i = 0; i < N; i++)
calc(i);
printf("%d\n", ans);
return 0;
}
思路： 1985也可以用1986的程序改改就行了。 但是觉得不用什么算法也是可以做出1985的。 想了一下，发现： 路径的最大值一定存在于两个叶子节点中。 如果只有一个叶子，那整个树就是一条直线了。 由于我们只是考虑叶子节点。那么对于每一个非叶子节点，我们只需要找出它下面的所有节点中，离它最远的两个叶子就行了。 这两个叶子节点的距离也就有可能成为答案。 对于每个点，我们只需要保存一个值，就是该点下面的所有节点中，距离它最远的一个叶子节点，和它的距离。 对于每个点，遍历完它的孩子之后，就知道“离它最远的两个叶子的距离”了。 注意： 代码里需要处理“一条直线连着几个点”这种情况，将这样的几个点缩成一个点比较好。不做这个处理一定会爆栈。最后一个数据是一条直线。（阴险） 这份代码跑了141MS，还算可以，呵呵。应该比直接用lca要快。
#include <stdio.h>
#define MAX_N 40032
struct edge_node {
struct edge_node *next;
int idx, len;
};
struct edge_node edges[MAX_N*2];
struct tree_node {
struct edge_node *edge;
int visited;
};
struct tree_node tree[MAX_N];
int max_val;
__inline void add_edge(int idx, int a, int b, int len)
{
struct edge_node *e = &edges[idx];
e->idx = b;
e->len = len;
e->next = tree[a].edge;
tree[a].edge = e;
}
int dfs(int idx)
{
struct edge_node *e;
int sum, cnt, arr[2], r;
sum = 0;
while (1) {
tree[idx].visited = 1;
cnt = 0;
for (e = tree[idx].edge; e; e = e->next)
cnt += !tree[e->idx].visited;
if (!cnt)
return sum;
if (cnt > 1)
break;
for (e = tree[idx].edge; tree[e->idx].visited; e = e->next);
sum += e->len;
idx = e->idx;
}
arr[0] = arr[1] = 0;
for (e = tree[idx].edge; e; e = e->next) {
if (tree[e->idx].visited)
continue;
r = dfs(e->idx) + e->len;
if (r >= arr[1]) {
arr[0] = arr[1];
arr[1] = r;
} else if (r >= arr[0])
arr[0] = r;
}
r = arr[0] + arr[1];
if (r > max_val)
max_val = r;
return arr[1] + sum;
}
int main()
{
int m, n, a, b, len, i;
char str[16];
freopen("e:\\test\\in.txt", "r", stdin);
scanf("%d%d", &n, &m);
for (i = 0; i < m*2; i += 2) {
scanf("%d%d%d%s", &a, &b, &len, str);
add_edge(i, a, b, len);
add_edge(i + 1, b, a, len);
}
for (i = 1; i <= n; i++) {
if (tree[i].visited)
continue;
a = dfs(i);
if (a > max_val)
max_val = a;
}
printf("%d\n", max_val);
return 0;
}
摘要: 以前没见过“最近公共祖先”这一类的题啊。长见识了，呵呵。解法基本上就是http://www.cppblog.com/varg-vikernes/archive/2010/03/10/109355.html这篇文章里面提到的两种方法。两种方法的解法都非常精妙！最后程序写出来：Tarjan 3372K 219MSDFS+RMQ 7992K 329MS代码Tarjan：... 阅读全文
|