|
|
Introduction

|
Hidden surface removal is among the biggest problems when writing a 3D engine.
I struggled with it since the very beginning of writing 3D engines and still have no satisfactory solution to it. The ideal visibility detection scheme would allow unlimited data, extremely dynamic worlds and would have zero overdraw. The first 3d engine which implements these three demands still has to be written.
The Z buffer for example allows dynamical worlds and even crossing faces, but it suffers from immense overdraw. The BSP-tree on the other hand, if well implemented, has no overdraw at all but needs that much pre-processing that dynamical worlds are a definite nono.
It wasn't until recently i first heard of the octree, and I must admit i was struck by it's simplicity. I never actually implemented this structure and therefore I will present no pseudo code at all. This explanation is merely an attempt to make it more clear to people who have never heard of it. Besides, if you really understand the structure, then implementation is a piece of cake. |
The Octree Structure

|
Our virtual world or level is actually nothing more then a soup of polygons. Some of you people might have thrown in a couple of curves and voxels but most of it will be polygons. Here it is:

Fig 1. Our little level.
In the picture I just built a simple level containing no more than 250 polys. Now imagine a cube surrounding the world like in the next image:
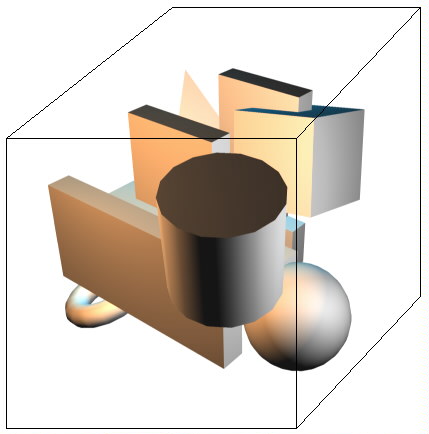
Fig. 2. Our little level surrounded by a cube.
Now it isn't hard to see that this cube can be divided into eight smaller cubes, hence the name octree. Take a look at this picture:

Fig 3. Our little level with the surrounding cube subdivided.
Call the larger cube the parent and the smaller cubes the children. On their turn subdivide each children into eight smaller cubes, and you will notice we are creating a tree where each node has eight children.
There is still one little problem left. When should we stop dividing cubes into smaller ones? There are two possible solutions. The first one is to stop when a cube has some size smaller then a fixed number. The second one is more common. You might have noticed that every child has less polygons then it's parent. The trick is to stop subdividing when the number of polygons in a cube is smaller then some fixed number. |
Creating The Octree

|
Trees are recursion, recursion is trees. It is as simple as that. If you have a correct definition of you cubeNode it is very easy to create an octree recursively. First of all you check all polygons against the boundarys of the cube. This is very simple cause these boundaries are all axis aligned. This means that the cube has six plane equations, which are:
1. X = Q.X
2. Y = Q.Y
3. Z = Q.Z
4. X = Q.X + cubeSize
5. Y = Q.Y + cubeSize
6. Z = Q.Z + cubeSize
Where Q is the position of one corner of the cube. This are very easy equations and the all parent polygons can very easily be checked against them.
It could occur that a polygon crosses a cube boundary. Again two possible solution are at hand. First of all we could clip the polygon against the cube, which is simple, because of the axis aligned boundarys. On the other hand we could put the polygon in all cubes it is in. This means that some cubes can contain the same polygons. In order to prevent us from drawing one poly more than one time we should have a flag on each polygon which will be set if the poly is drawn for the first time.
The implementation of an octree is very straight forward. I haven't done it myself yet, but I will soon. It is all matter of recursion. In order to construct a tree, the first thing you should think of is recursion. Whether we are talking about binary trees, quad trees or octrees, it doesnt matter, just build the darn thing recursively. So have a class definition of one cubeNode and put the creation of the tree in it's constructor. In this constructor you will call the constructor itself for smaller cubes.
|
The Purpose Of The Octree

|
An octree is actually nothing more then a data structure. It can be used for very different things. It is not only handy for visibility detection but also for collision detection, realtime shadows and many more things. The most important thing to understand about octrees is that if a parent is not important then it's children aren't either. Let's makes this a little bit more clear with an example.
We will do this in 2d, which therefore resembles a quadtree, but with some imagination it can very easily be extended to 3d. Here we test the cubes (squares) against the viewing frustrum. Take a look at the next picture:
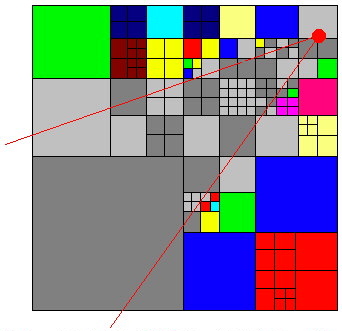
Fig 4. An octree from the top and a viewing frustrum.
In this picture a colored square that has one color was dumped without checking it�s children. As you can see some squares had to be checked all the way to the final node, but some large squares could be dumped at once. The colored squares are the ones that are outside the viewing frustrum and the greyscale ones are the one inside the viewing frustrum. As you can see this is actually a worst case scenario because the viewing frustrum crosses the middle of the surrounding square and therefore all the four children have to be checked.
You could also apply the octree to many other things. Collision detection for example. Just check in which cube your bounding sphere or box is and you will only have to check against those faces. There are many more examples. |
Conclusion

|
There is already a lot written about octrees. I tried to give my view on them in the hope somebody might read this. As you can see octrees are way easier to implement than BSP-trees (although some disagree) while offering a better structure. The main point about an octrees is that when a parent is discarded so are it's children. Actually that is all there is to it.
Code clean, play Goldeneye and go vegetarian.
Jaap Suter a.k.a ......... |
译文:
1、引言(Introduction)
隐面移除是写3D引擎时候最大的问题之一。
Hidden surface removal is among the biggest problems when writing a 3D engine.
在我写3D引擎的开始阶段就开始和它斗争并且一直没有满意的解决方法。理想的可见检测方案应当做到允许(使用)无限的数据、大动态的世界和零重画。第一流的3D引擎一直在追求实现这3个要求。
I struggled with it since the very beginning of writing 3D engines and still have no satisfactory solution to it. The ideal visibility detection scheme would allow unlimited data, extremely dynamic worlds and would have zero overdraw. The first 3d engine which implements these three demands still has to be written.
Z buffer允许动态世界以及即使是交叉的面,但是得忍受大量的重画。另一方面,BSP树如果能够被很好的实现,可以避免重画,但是它需要大量的预处理计算而且不适合动态世界。
The Z buffer for example allows dynamical worlds and even crossing faces, but it suffers from immense overdraw. The BSP-tree on the other hand, if well implemented, has no overdraw at all but needs that much pre-processing that dynamical worlds are a definite nono.
直到最近我第一次听说了八叉树(Octree),我必须承认我被它的简易性“狠狠地打了一下儿”。我从来没有真正地去实现这个结构,因此我不会去实现一些代码。这个解释只是想让从没有听说过八叉树的人感到更清晰易懂。如果你真的了解了这个结构(Octree),实现它只是一个小意思。
It wasn't until recently i first heard of the octree, and I must admit i was struck by it's simplicity. I never actually implemented this structure and therefore I will present no pseudo code at all. This explanation is merely an attempt to make it more clear to people who have never heard of it. Besides, if you really understand the structure, then implementation is a piece of cake.
2、八叉树的结构(The Octree Structure)
我们的实际‘世界’或者说是关卡只不过是一些多边形。你们或许在其中加入了一些曲面(Curves)和Voxels(地形实现方法的一种),但是大多数也都是多边形。
Our virtual world or level is actually nothing more then a soup of polygons. Some of you people might have thrown in a couple of curves and voxels but most of it will be polygons. Here it is:
 |
| 图1 |
图1:我们设计的小型关卡。
Fig 1. Our little level.
在这张图片中我建立了一个不超过250个多边形的‘关卡’。现在想象有一个包围了这个世界的立方体,像下一张图片那样。
In the picture I just built a simple level containing no more than 250 polys. Now imagine a cube surrounding the world like in the next image:
 |
| 图2 |
图2:我们设计的关卡被一个立方体所包围着。
Fig. 2. Our little level surrounded by a cube.
现在不难看出这个立方体可以被八等分为八个小些的立方体,所以才叫八叉树。看看这张图:
Now it isn't hard to see that this cube can be divided into eight smaller cubes, hence the name octree. Take a look at this picture:
 |
| 图3 |
图3:对围绕着关卡的立方体进行细分。
Fig 3. Our little level with the surrounding cube subdivided.
大点儿的这个立方体被叫做‘父亲’小些的立方体叫做‘孩子’。处理每个‘孩子’的时候,再为更小的八个立方体,你会发现我们在创建一个每个节点有八个子节点(孩子)的树。
Call the larger cube the parent and the smaller cubes the children. On their turn subdivide each children into eight smaller cubes, and you will notice we are creating a tree where each node has eight children.
还有一个小问题。什么时候我们该结束细分的过程呢?有两个可行的解决方法。第一个是当一个立方体的尺寸已经比一个预定的固定值小的时候。第二个更普通。你可以注意到每个‘孩子’都比他的‘父亲’有更少的多边形。这就是说:当一个立方体包含的多边形数量比一个预定的固定值少的时候停止细分。
There is still one little problem left. When should we stop dividing cubes into smaller ones? There are two possible solutions. The first one is to stop when a cube has some size smaller then a fixed number. The second one is more common. You might have noticed that every child has less polygons then it's parent. The trick is to stop subdividing when the number of polygons in a cube is smaller then some fixed number.
3、创建八叉树(Creating The Octree)
树是递归的,递归的是树。就那么简单。如果你正确的定义了你的立方体节点,那么递归地创建一个八叉树是很容易的。首先,检查所有的多边形(多边形上位置最外面的点作为)立方体的边界。这很简单因为所有边界都是和坐标轴对其的。这意味着立方体有六个平面方程,分别是:
Trees are recursion, recursion is trees. It is as simple as that. If you have a correct definition of you cubeNode it is very easy to create an octree recursively. First of all you check all polygons against the boundarys of the cube. This is very simple cause these boundaries are all axis aligned. This means that the cube has six plane equations, which are:
- 1. X = Q.X
- 2. Y = Q.Y
- 3. Z = Q.Z
- 4. X = Q.X + cubeSize
- 5. Y = Q.Y + cubeSize
- 6. Z = Q.Z + cubeSize
在这里Q是立方体一个顶角的位置。这是个很简单的方程,而且所有的父亲多边形可以容易地用这些方程来检测。
WhereQ is the position of one corner of the cube. This are very easy equations and the all parent polygons can very easily be checked against them.
一个多边形穿过了一个立方体边界这样的事情是会发生的。再一次,有两个解决方案可用。首先我们可以沿着立方体剪切这个多边形,这也是很简单的,因为(立方体的)边界是与坐标轴对齐的。还有,我们可以把一个多边形放在所有它所在的立方体里面。这就意味着一些立方体可能包含着同一个多边形。为了防止重画一个多边形,我们应当在每一个多边形上做一个标记,当多边形第一次被画的时候,设置这个标记(当然画之前也要检查这个标记啦,不过肯定影响效率。
It could occur that a polygon crosses a cube boundary. Again two possible solution are at hand. First of all we could clip the polygon against the cube, which is simple, because of the axis aligned boundarys. On the other hand we could put the polygon in all cubes it is in. This means that some cubes can contain the same polygons. In order to prevent us from drawing one poly more than one time we should have a flag on each polygon which will be set if the poly is drawn for the first time.
实现一个八叉树是很简单明了的事情,我还没有自己做过,但是我不久会做的。只不过是递归而已。为了构造一个树,第一件你该想的事情就是递归。不管我们讨论的是二叉、四叉还是八叉树,都没有区别,都是递归的方法。所以定义一个立方体节点的类,在构造函数里面写上创建树的代码。在这个构造函数里面,你会调用到更小立方体的构造函数。
The implementation of an octree is very straight forward. I haven't done it myself yet, but I will soon. It is all matter of recursion. In order to construct a tree, the first thing you should think of is recursion. Whether we are talking about binary trees, quad trees or octrees, it doesnt matter, just build the darn thing recursively. So have a class definition of one cubeNode and put the creation of the tree in it's constructor. In this constructor you will call the constructor itself for smaller cubes.
4、八叉树的用途(The Purpose Of The Octree)
一个八叉树实际上就是一个数据结构。它可以用做不同的事情。不仅仅对于‘可见检测’来说很方便,还有实时阴影以及其它方面。理解八叉树过程中最重要的事情是:如果一个‘父亲’节点是‘没用’的,那么他的‘孩子’节点也同样。让我们举个例子让它更清楚。
An octree is actually nothing more then a data structure. It can be used for very different things. It is not only handy for visibility detection but also for collision detection, realtime shadows and many more things. The most important thing to understand about octrees is that if a parent is not important then it's children aren't either. Let's makes this a little bit more clear with an example.
我们用2D来表示它,这样就很像一个四叉树,但是想象一下它也可以很容易的扩展到3D上。在这里我们沿着视锥(viewing frustrum)检测立方体(正方形)。
We will do this in 2d, which therefore resembles a quadtree, but with some imagination it can very easily be extended to 3d. Here we test the cubes (squares) against the viewing frustrum. Take a look at the next picture:
 |
| 图4 |
图4:顶部视锥内的八叉树。
Fig 4. An octree from the top and a viewing frustrum.
在这个图片中,彩色的正方形是没有(没必要)检测它的‘孩子’的。就像你看到的那样一些正方形(灰色的一些)被检测直到最终节点,但是一些大的正方形只被涂了一种颜色。那些彩色的正方形就是超出了视锥范围的,灰色的是在视锥范围内的。就像你看到的那样,这确实是最糟糕的一种情况,因为视锥穿过了包围正方形的中央,所以所有的四个‘孩子’都得被检测。
In this picture a colored square that has one color was dumped without checking it抯 children. As you can see some squares had to be checked all the way to the final node, but some large squares could be dumped at once. The colored squares are the ones that are outside the viewing frustrum and the greyscale ones are the one inside the viewing frustrum. As you can see this is actually a worst case scenario because the viewing frustrum crosses the middle of the surrounding square and therefore all the four children have to be checked.
你可以应用八叉树到很多别的地方。例如碰撞检测。只检查你的碰撞球或者碰撞盒子所在的立方体,而且只需要检测那些面。还有更多的例子。
You could also apply the octree to many other things. Collision detection for example. Just check in which cube your bounding sphere or box is and you will only have to check against those faces. There are many more examples.
5、结论(Conclusion)
关于八叉树已经写了很多了。我设法表述自己对它的看法,并且希望有人会读到它。就像你看到的那样,当提供好的结构的时候,八叉树比BSP树更容易实现(有人持异议)。主要的一点是:当一个‘父亲’节点被丢弃的时候,他的‘孩子’节点也同样被丢弃。实际上这就是全部。
There is already a lot written about octrees. I tried to give my view on them in the hope somebody might read this. As you can see octrees are way easier to implement than BSP-trees (although some disagree) while offering a better structure. The main point about an octrees is that when a parent is discarded so are it's children. Actually that is all there is to it.
Code clean, play Goldeneye and go vegetarian. Jaap Suter a.k.a .........

|