一个非确定自动机( NFA) 在读入符号串之后,并不确切地知道自动机处于哪个状态。但可以肯定一定处于状态集中的某一状态。该状态集记做 {q1,q2,…qk} 。而一个等价的确定自动机( DFA) 读入同样的 w 一定处于某个确定的状态上。这样,都是读入同样的 w , DFA 到达某一个状态,而 NFA 到达某一个状态集。由 w 的任意性,可将 NFA 的所有的状态集和 DFA 的状态一一对应起来。这种对应的前提就是能识别同样的输入串。即 L(M1)=L(M2) 。
显然,后一个状态集是依赖于前一个状态集的,是在前一个状态集的基础上,(其内任意结点)经过同一条路径到达的。下面是一个简单的例子:
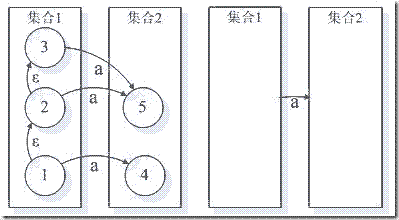
可以看出,其核心是将 NFA 状态集归并为 DFA 中的状态。在 NFA 中,无论是从 1 到 4 ,还是 1 到 5 ,作为集合来讲都是集合 1 到集合 2 ,最为重要得是经过的条件都是 a 。因而从识别语言的效果是一样的。这使得这些弧合并成为可能。
考虑集合覆盖的情况。
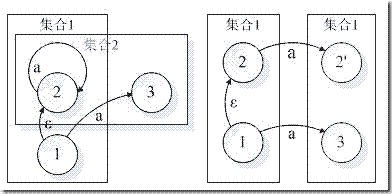
一个结点属于第一个集合又同时属于第二个集合。这种情况不一定好理解。但如果从路径的历史的角度进一步区分,即不同的时间经过同一个结点,将其看成是不同的状态。按照这种时空的角度进一步区分,得到右图。这和图 1 是类似的。
再来看看带有终态结点的情况:
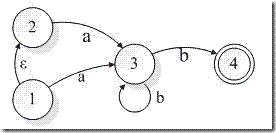
ab , abb 均为该 NFA 识别的句子,其转换如下:
| | I a | Ib |
| A{1,2} | {3} | Φ |
| B{3} | Φ | {3,4} |
| C{3,4} | Φ | {3,4} |
从某种意义上说。 NFA 中的状态 3 在 DFA 中被分离成两部分,当首次到达 3 时应该是状态 B ,而第二次以后再到达 3 则应该属于状态 C 。
根据规则, C{3,4} 为 DFA 的终态,但在 NFA 中,只有 4 为终态, C 中仍然有 3 为非终态,若有路径 1 à 3 à 3 映射到 DFA 中也是 A à B à C ,何解?
这里面最关键的是:对任意一个句子,总可以在两个图中分别找到一条路径,形成对应关系。并不是说 NFA 中的每条路径都要和 DFA 中的每条路径一一对应。
当识别句子 ab 时,选择由 3 直接到达 4 的路径。当识别句子 abb 时,则在状态 3 循环一次再到达 4 。
现在设想,通过 1 à 3 à 3 经过的路径也是 ab 。但此时并未到达终态。可以说,在到达 C 中的 3 时,必然选择了两个 b 以上的句子。
而这样的路径与选择句子有关系。
对于 NFA 能识别的句子,在 DFA 中也能识别。
对于 NFA 不能识别的句子,在 DFA 中也不能识别。