woaidongmao

综述

下推自动机比有限状态自动机复杂：除了有限状态组成部分外，还包括一个长度不受限制的栈；下推自动机的状态迁移不但要参考有限状态部分，也要参照栈当前的状态；状态迁移不但包括有限状态的变迁，还包括一个栈的出栈或入栈过程。下推自动机可以形象的理解为，借由加上读取一个容量无限堆栈的能力，扩充一个能做ε-转移的非确定有限状态自动机。

下推自动机存在“确定”与“非确定”两种形式，两者并不等价。（对有限状态自动机两者是等价的）

每一个下推自动机都接受一个形式语言。被“非确定下推自动机”接受的语言是上下文无关语言。

如果我们把下推自动机扩展，允许一个有限状态自动机存取两个栈，我们得到一个能力更强的自动机，这个自动机与图灵机等价。

下推自动机作为一个形式系统最早于1961年出现在 Oettinger 的论文中。它与上下文无关文法的等价性是由乔姆斯基于1962年发现的。

[编辑] 形式定义

PDA 形式定义为 6-元组:

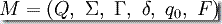这里的

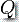• 是状态的有限集合
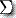• 是输入字母表的有限集合
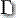• 是栈字母表的有限集合
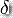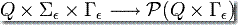• : 是转移函数
• q₀ 是“开始状态”
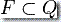• 是“接受状态”的集合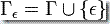
• 
• 

计算定义 1

对于任何 PDA 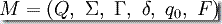，计算路径是一个有序的(n+1)-元组 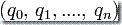，这里的 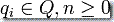，它满足如下条件:

(i) 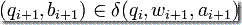对于 i = 0, 1, 2,......, n-1,

这里的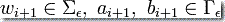

(ii) 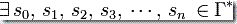使得

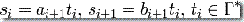
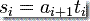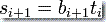在直觉上，PDA 在计算过程中任何一点上都面对着多种可能性，从栈顶读一个符号并把它替代为另一个符号，从栈顶读一个符号并删除它而不替换，不从栈顶读任何符号但压入另一个符号进去，或什么都不做。所有这些都同时由等式 和 来支配。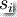 是紧接在第 i+1 次转移移动之前的栈内容，而 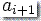是要从栈顶去除的符号。 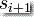是紧接在第 i+1 次转移移动之后栈内容，而 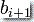是在第 i+1 次转移移动期间要增加到栈上的符号。

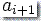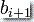和 二者都可以 。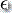

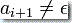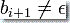如果 而 ，则 PDA 从栈读一个符号并把它替代为另一个符号。

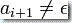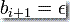如果 而 ，则 PDA 从栈读一个符号并删除它而不替换。

如果 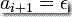而 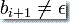，则 PDA 简单的增加一个符号到栈上。

如果 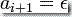而 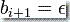，则 PDA 保持栈不变动。

注意当 n=0 时，计算路径就是单元素集合 。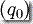

计算定义 2

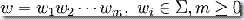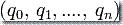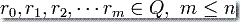对于任何输入 ，M 接受 w，如果存在计算路径 和有限序列 ，使得

(i) 对于每个 i = 0, 1, 2,...m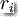， 都在计算路径上。就是说

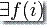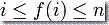这里的 使得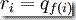

(ii) 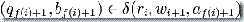对于每个 i = 0, 1, 2,...m-1。

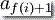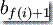这里的 和 定义同于计算定义 1。

(iii) 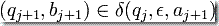，如果

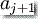这里的 和 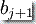定义同于计算定义 1。

(iv) 且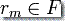

注意上述定义不提供测试空栈的机制。要这么做你需要在所有计算开始前在栈上写一个特殊符号，使得 PDA 可以在检测到这个符号的时候有效的识别出栈已经空了。形式的说，实现它可通过介入转移 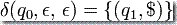这里的 $ 是特殊符号。

[编辑] 例子

下面是识别语言 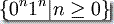的 PDA 的形式描述:

• 

• 

• 

• 

• 

• 

• 

• 

• 

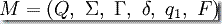
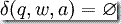• 对于任何其他状态、输入和栈符号的值。

[编辑] 理解计算过程

下面展示上述 PDA 如何计算不同的输入字符串。

(a) 输入字符串 = 0011

(i) 写 δ(q₁, ε, ε) 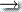(q₂, $) 来表示 (q₂, $) 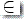δ(q₁, ε, ε)

s₀ = ε, s₁ = $, t = ε, a = ε, b = $

设置 r₀ = q₂

(ii) δ(r₀, 0, ε) = δ(q₂, 0, ε) 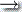(q₂, 0)

s₁ = $, a = ε, t = $, b = 0, s₂ = 0$

设置 r₁ = q₂

(iii) δ(r₁, 0, ε) = δ(q₂, 0, ε) 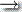(q₂, 0)

s₂ = 0$, a = ε, t = 0$, b = 0, s₃ = 00$

设置 r₂ = q₂

(iv) δ(r₂, 1, 0) = δ(q₂, 1, 0) 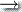(q₃, ε)

s₃ = 00$, a = 0, t = 0$, b = ε, s₄ = 0$

设置 r₃ = q₃

(v) δ(r₃, 1, 0) = δ(q₃, 1, 0) 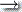(q₃, ε)

s₄ = 0$, a = 0, t = $, b = ε, s₅ = $

(vi) δ(q₃, ε, $) 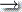(q₄, ε)

s₅ = $, a = $, t = ε, b = ε, s₆ = ε

设置 r₄ = q₄

因为 q₄ 是接受状态，0011 被接受。

作为总结，计算路径 = (q₁, q₂, q₂, q₂, q₃, q₃, q₄)

而 (r₀, r₁, r₂, r₃, r₄) = (q₂, q₂, q₂, q₃, q₄)

(b) 输入字符串 = 001

计算移动 (i), (ii), (iii), (iv) 将必定同于情况 (a)，否则，PDA 在到达 (v) 之前就已经进入死胡同。

(v) δ(r₃, ε, a) = δ(q₃, ε, a)

因为 s₄ = 0$，要么 a = ε 要么 a = 0

在任何一种情况下，δ(q₃, ε, a) =

因此计算在 r₃ = q₃ 进入死胡同，这不是接受状态。所以 001 被拒绝。

(c) 输入字符串 = ε

设置 r₀ = q₁, r₁ = q₁

δ(r₀, ε, ε) 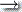(q₁, ε)

因为 q₁ 是接受状态，ε 被接受。

[编辑] 广义下推自动机(GPDA)

GPDA 是在一个步骤内写入整个字符串到栈上或从栈上去除整个字符串的 PDA。

GPDA 形式定义为 6-元组

这里的 Q, 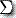, , 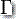q₀ 和 F 的定义同于 PDA。

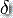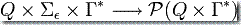: 是转移函数。

GPDA 的计算规则同于 PDA，除了 a_i+1 和 b_i+1 现在是字符串而不是符号之外。

GPDA 和 PDA 是等价的，如果一个语言可被一个 PDA 识别，它也可被一个 GPDA 识别，反之亦然。

可以使用下列模拟公式化对 GPDA 和 PDA 的等价性的一个分析式证明:

设 δ(q₁, w, x₁x₂...x_m) (q₂, y₁y₂...y_n) 是 GPDA 的转移。

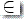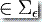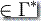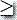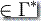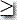这里的 q₁, q₂ Q, w , x₁x₂...x_m , m0, y₁y₂...y_n , n0。

构造 PDA 的下列转移:

δ^'(q₁, w, x₁) (p₁, ε)

δ^'(p₁, ε, x₂) (p₂, ε)

δ^'(p_m-1, ε, x_m) (p_m, ε)

δ^'(p_m, ε, ε ) (p_m+1, y_n)

δ^'(p_m+1, ε, ε ) (p_m+2, y_n-1)

δ^'(p_m+n-1, ε, ε ) (q₂, y₁)

[编辑] 参见

• 确定下推自动机
• 有限状态自动机
• 上下文无关文法

[编辑] 外部链接

• non-deterministic pushdown automaton, on Planet Math.
• JFLAP, simulator for several types of automata including nondeterministic pushdown automata

[编辑] 参考书目

• 《自动机理论、语言和计算导引》，John E. Hopcroft，Jeffery D. Ullman，徐美瑞译，洪加威校，科学出版社，1986年
• Michael Sipser（1997）．Introduction to the Theory of Computation．PWS Publishing．ISBN 0-534-94728-X．  Section 2.2: Pushdown Automata, pp.101–114.

取自"http://zh.wikipedia.org/w/index.php?title=%E4%B8%8B%E6%8E%A8%E8%87%AA%E5%8A%A8%E6%9C%BA&variant=zh-cn"