参考原文:
http://tech.idv2.com/2006/05/08/parse-regex-with-dfa/
程序编译的第一个阶段是词法分析,即把字节流识别为记号(token)流,提供给下一步的语法分析过程。而识别记号的方法就是正则表达式的分析。本文介绍利用有限自动机分析表达式的方法。
· 概念
· 将正则表达式转换为NFA(Thompson构造法)
o 算法
o 性质
o 示例
· 将NFA转化为DFA
o 算法
o 示例
· NFA和DFA的效率
概念
记号
有字母表中的符号组成的有限长度的序列。记号s的长度记为|s|。长度为0的记号称为空记号,记为ε。
有限自动机(Finite State Automaton)
为研究某种计算过程而抽象出的计算模型。拥有有限个状态,根据不同的输入每个状态可以迁移到其他的状态。
非确定有限自动机(Nondeterministic Finite Automaton)
简称NFA,由以下元素组成:
1. 有限状态集合S;
2. 有限输入符号的字母表Σ;
3. 状态转移函数move;
4. 开始状态 sSUB{0};
5. 结束状态集合F,F ∈ S。
自动机初始状态为sSUB{0},逐一读入输入字符串中的每一个字母,根据当前状态、读入的字母,由状态转移函数move控制进入下一个状态。如果输入字符串读入结束时自动机的状态属于结束状态集合F,则说明该自动机接受该字符串,否则为不接受。
确定有限自动机(Deterministic Finite Automaton)
简称DFA,是NFA的一种特例,有以下两条限制:
1. 对于空输入ε,状态不发生迁移;
2. 某个状态对于每一种输入最多只有一种状态转移。
将正则表达式转换为NFA(Thompson构造法)
算法
算法1 将正则表达式转换为NFA(Thompson构造法)
输入 字母表Σ上的正则表达式r
输出 能够接受L(r)的NFA N
方法 首先将构成r的各个元素分解,对于每一个元素,按照下述规则1和规则2生成NFA。 注意:如果r中记号a出现了多次,那么对于a的每次出现都需要生成一个单独的NFA。
之后依照正规表达式r的文法规则,将生成的NFA按照下述规则3组合在一起。
规则1 对于空记号ε,生成下面的NFA。
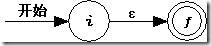
规则2 对于Σ的字母表中的元素a,生成下面的NFA。
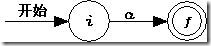
规则3 令正规表达式s和t的NFA分别为N(s)和N(t)。
a) 对于s|t,按照以下的方式生成NFA N(s|t)。
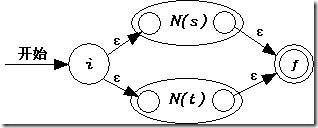
b) 对于st,按照以下的方式生成NFA N(st)。

c) 对于s*,按照以下的方式生成NFA N(s*)。
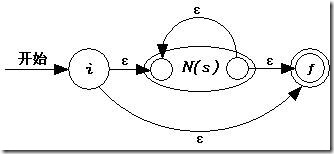
d) 对于(s),使用s本身的NFA N(s)。
性质
算法1生成的NFA能够正确地识别正则表达式,并且具有如下的性质:
1. N(r)的状态数最多为r中出现的记号和运算符的个数的2倍。
2. N(r)的开始状态和结束状态有且只有一个。
3. N(r)的各个状态对于Σ中的一个符号,或者拥有一个状态迁移,或者拥有最多两个ε迁移。
示例
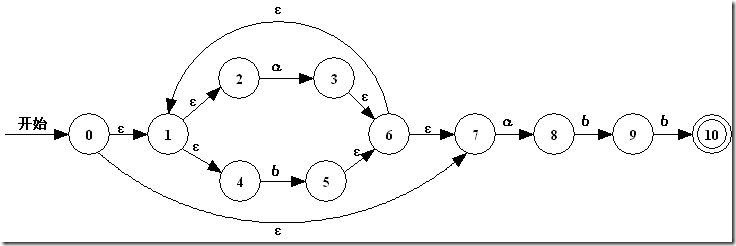
利用算法1,根据正则表达式 r=(a|b)*abb 可以生成以下的NFA。
将NFA转化为DFA
算法
使用以下的算法可以将NFA转换成等价的DFA。
算法2 将NFA转化为DFA
输入 NFA N
输出 能够接受与N相同语言的DFA D
方法 本算法生成D对应的状态迁移表Dtran。DFA的各个状态为NFA的状态集合,对于每一个输入符号,D模拟N中可能的状态迁移。
定义以下的操作。
| 操作 | 说明 |
| ε-closure(s) | 从NFA的状态s出发,仅通过ε迁移能够到达的NFA的状态集合 |
| ε-closure(T) | 从T中包含的某个NFA的状态s出发,仅通过ε迁移能够到达的NFA的状态集合 |
| move(T, a) | 从T中包含的某个NFA的状态s出发,通过输入符号a迁移能够到达的NFA的状态集合 |
令 Dstates 中仅包含ε-closure(s), 并设置状态为未标记;
while Dstates中包含未标记的状态T do
begin
标记T;
for 各输入记号a do
begin
U := ε-closure(move(T, a));
if U不在Dstates中 then
将 U 追加到 Dstates 中,设置状态为未标记;
Dtrans[T, a] := U;
end
end
ε-closure(T)的计算方法如下:
将T中的所有状态入栈;
设置ε-closure(T)的初始值为T;
while 栈非空 do
begin
从栈顶取出元素t;
for 从t出发以ε为边能够到达的各个状态u do
if u不在ε-closure(T)中 then
begin
将u追加到ε-closure(T)中;
将u入栈;
end
end
示例
将上面生成的NFA转化为DFA。
最初,Dstates内仅有ε-closure(0) = A = {0, 1, 2, 4, 7}。然后对于状态A,对于输入记号a,计算 ε-closure(move(A, a)) = ε-closure(move({0, 1, 2, 4, 7}, a)) = ε-closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8},即 B={1, 2, 3, 4, 6, 7, 8}, Dtran[A, a]=B。对于状态A,由输入记号b能够到达的仅有4->5,因此 C = ε-closure({5}) = {1, 2, 4, 5, 6, 7},即 Dtran[A, b] = C。
以此类推,可得到以下的状态和Dtran。
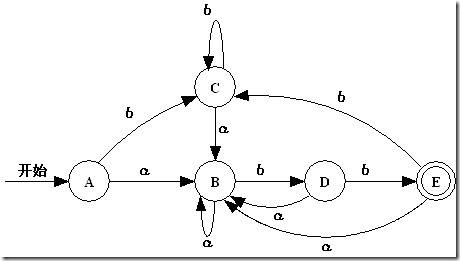
A = {0, 1, 2, 4, 7} D = {1, 2, 4, 5, 6, 7, 9}
B = {1, 2, 3, 4, 6, 7, 8} E = {1, 2, 4, 5, 6, 7, 10}
C = {1, 2, 4, 5, 6, 7}
| 状态 | 输入符号 |
| a | b |
| A | B | C |
| B | B | D |
| C | B | C |
| D | B | E |
| E | B | C |
由此得出DFA如下图所示。
NFA和DFA的效率
给定正则表达式r和输入记号序列x,判断r是否能够接受x。
使用NFA的情况下,由正则表达式生成NFA的时间复杂度为O(|r|),另外由于NFA的状态数最多为r的2倍,因此空间复杂度为O(|r|)。由NFA判断是否接受x时,时间复杂度为O(|r|×|x|)。因此,总体上处理时间与 r、x的长度之积成比例。这种处理方法在x不是很长时十分有效。
如果使用DFA,由于利用DFA判断是否接受x与状态数无关,因此时间复杂度为O(|x|)。但是DFA的状态数与正则表达式的长度呈指数关系。例如,正规表达式 (a|b)*a(a|b)(a|b)...(a|b),尾部有 n-1 个 (a-b)的话, DFA最小状态数也会超过 2SUP{n}。