最近得做一些跟自动机有关的东东,其中一部分可以简要地看作是由一套正则文法生成状态自动机的过程。
什么是正则表达式?
首先我们看看什么是正则表达式。这个东东呢,一般用于描述一个字符串的集合——直接说就是一个正则表达式可能可以匹配一大堆字符串,而这一大堆字符串可以形成一个集合,它们的共同特征就是可以被这个正则表达式匹配。就像去死去死团,但是不同的是去死去死团的团员的共同特征是不被任何异性所匹配——但是这没关系,我们不妨取去死去死团的补集就行了。
反正正则表达是很好啦,因为你只要用一点点在脏话里,就可以骂好多好多人,比如:
Mar(y|k|cus) is son of bitch.
真是非常de省力,唯一的缺点是可能对方不知道你在说什么。
好了,从上面我们可以看出正则表达式中的两个基本结构:
· 连结 (Concatenation),比如 bitch,由b, i, t, c, h连接而成
· 联合 (Union),比如 y|k|cus,可以认为是y或k或者cus
下面是第三个基本结构,被称为Kleene star (或者 Kleene 闭包)的。因为这个操作是Stephen Cole Kleene发明的。啊啊,其实正则表达式这个东西就是Kleene发明的。这个同学真是非常的牛B,因为他是更加牛B的 阿隆佐 - 丘奇 ( Alonzo Church )——历史上和阿兰 - 图灵 ( Alan Turing ) 并称的人物——的学生。有多牛B呢,这个Kleene还和他的老师,还有图灵,就递归论发表了论文,奠定了可计算理论的根基。啊哈哈哈,真是牛B啊。
嗯,所谓Kleene Star的例子就是这样的。
· Kleene Star,比如a*,可以接受空串和若干个a连结组成的串
当然咯,还有一些别的操作,比如我们知道的+,?,集合[]等等,但是这些操作都可以通过上面三个基本操作的组合来完成。
比如+,a+可以认为是aa*
什么是NFA?
要说NFA嘛,我得先说说DFA。所谓DFA,就是Deterministic Finite state Automata的简称。是状态机的一种。通俗的说,就是一大堆状态的集合,里面有一个初始状态和若干终止状态,每个状态可以有若干个输出边前往别的状态。但是要求每个状态的同一种输出边至多只有一个,所以自动机被称为是”Deterministic”的。
比如下面这个例子:
表述的是一个电灯de开关,这个开关每按一下就从’开’状态转换到’关’状态,或者从’关’状态转换到’开’状态。而为了从环保角度出发,在’关’状态才被认为是终止态。
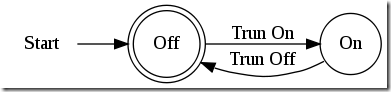
上面的自动机呢,就可以描述这个灯泡的行为模式,或者说可以描述电灯的状态转换过程。输出边就是’开’或者’关’的动作,或者说这个灯泡的开关,只接受这两种动作:“Trun On”,“Trun Off”。而”Trun On”动作只会导致灯的状态变成“On”,“Trun Off”动作只会导致灯的状态变成“Off”,这是确定的,你的外婆都可以预料到的。所以说DFA是确定有限状态自动机。
现在可以说NFA了。这个NFA嘛,全称是Non-deterministic Finite state Automata。也是状态自动机的一种。确切地说,刚才的DFA是NFA的一个子集。和DFA唯一的区别就是他是”Non-deterministic”的,哈,非确定的,每个状态的同一种输出边可以不止一个。
还是用刚才的例子。现在假设我们的电灯有一种新的状态咯~:坏掉了。灯丝被过大的电流烧断了,听上去遭透了,因为一”Trun On”就得准备换灯泡了:
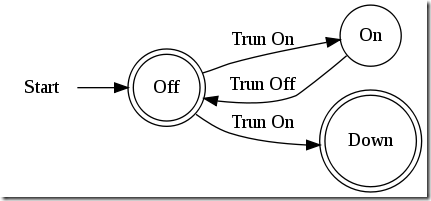
但是我们没法确定的知道哪一次Trun On会导致灯泡坏掉,使得灯泡进入”Down”状态的那次“开”操作看上去跟你昨天开灯的那次操作一模一样(严格的说,每一次点亮灯泡都会导致灯丝的状态发生变化,但是在此简化了)
所以从状态”Off”出来的输出边中,”Trun On”有两条,这就导致没法根据当前状态和输出边确定下一状态,这就是为什么称为非确定性有限自动机的原因。
如何转换?
刚才Shellex说了,正则表达式有三种基本结构。如果能先将这三种基本结构转换成对应的NFA,然后在用这三种基本结构去拼装成完整的NFA是不是很省力呢?
下面就是三种基本正则表达式的NFA
ab:

a*:
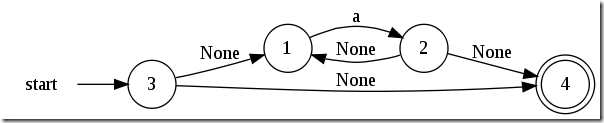
a|b:
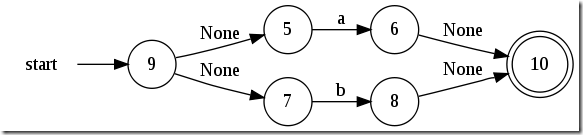
里面出现了一种叫“None”的边。这个不代表这个边是字面上的“None”,而是指这个边是个空边。也就是说任何“动作”都可以从这个边进入下一个状态。它的学名叫 epsilon 边,一般表示成’ε’,Shellex这里表示成“None”了。
下面我们来考虑正则表达式到NFA转换。给出一个正则串的输入,得到一个NFA的输出。被广泛采用的是Thompson Algorithm,也就是所谓的子集算法。该算法的发明人应该就是写ed编辑器的那个Thompson大牛。该算法的实现和算术表达式的求值非常的类似,需要一个符号栈存放操作符,一个自动机栈存放生成的自动机。算法结束后,可以从自动机栈中Pop一个最终的结果。
比如对于正则表达式(a|b)*cd,求值过程如下:
PUSH a To automaton stack
PUSH b To automaton stack
UNION
STAR
PUSH c To automaton stack
CONCAT
PUSH d To automaton stack
CONCAT
POP result
里面的UNION,STAR 和 CONCAT就是三种基本结构的生成操作了。而这三种基本操作的实现是这样的:
Star:
POP T from automaton stack
CREATE state A, B
ADD transition from A to B with 'ε'
ADD transition from A to T.entry with 'ε'
ADD transition from T.exit to A with 'ε'
ADD transition from T.exit to B with 'ε'
ADD state A, B to T
PUSH T to automaton stack
Concat:
POP F, S from automaton stack
ADD transition from F.exit to S.entry with 'ε'
JOIN S to F
SET F.exit = S.exit
SET F.inputSet += S.inputSet
PUSH F to automaton stack
Union:
POP F, S from automaton stack
CREATE state A, B
ADD transition from A to F.entry with 'ε'
ADD transition from A to S.entry with 'ε'
ADD transition from T.exit to B with 'ε'
ADD transition from T.exit to B with 'ε'
JOIN S to F
ADD state A, B to T
SET F.exit = S.exit
SET F.inputSet += S.inputSet
PUSH F to automaton stack