wujiawei@HIT

2010年10月4日 #

2010 哈尔滨赛区regional总结

哈尔滨赛区regional总结

吴嘉伟 @ HIT_Explorer

哈尔滨赛区比赛刚刚结束，我们队伍Explorer在这次比赛中通过了6题获得银牌，下面是我对整个比赛的一些总结。

哈尔滨赛区是第一场的比赛，在比赛之前我们自己进行了一些训练，做了08年的两个regional赛题，在配合上和比赛的题目上得到了一些练习。

在正式比赛上，我们比赛时分开看题目，然后找到最简单的题，看到之后觉得很简单，后来怕有陷阱，深思熟虑之后同时也有很多队伍过了，就果断的写，一次提交通过。然后我在比赛中发现了一个求两个圆柱体体积并的题目，看上去是一个求积分的题目，于是我开始推导公式，然后在一番努力之后求得到了答案的表达式，但是考虑之后发现还是有一半的情况没有考虑好。那个题目看了很久，然后后来看到眼花，于是和队友讨论一下，希望能共同讨论一下特殊情况的处理，结果发现图形实在是很不容易想象，结果一直卡着，尝试的方法也WA了，很是郁闷，这时候场上大多数已经是4题的了，于是我们开始继续找到大家过得比较多的，发现A题与我们练习做的一道题目极为类似，于是两位队友商量了一下就搞定了，然后队友经过一番努力将H那个网络流题目过了，此时我还在纠结那个积分的问题，想着想着就绕进去了。场上大多数是5题看了一下rank，排在21左右。然后大家在期待我的积分结果，后来积出了一个式子发现结果很难得到，然后两个队友对其他两题很有信心便让我再仔细想想然后他们先做别的，结果DebugCool在改过几次之后把G题过掉然后，杨靖剩下的时间做J题，我的I题一直在wa，后来也是打扰了杨靖不少时间，否则最后J题应该会过的，只差半分钟没交上最后的版本。觉得很遗憾，也很内疚，责任主要在我，身为队长首先对题的难度没有很好把握，也没有像以前一样给队友特别多的帮助，在简单题目上花费时间比较多。需要回去好好总结一下，当时比赛的时候也是有些慌了，遇到题目想的容易复杂，然后思路就混乱了，以后还是要多多练习，最好是在比赛中得到锻炼，然后认真做好每一题，认真总结每一次。

这次比赛中能看到一些问题，哈尔滨赛区是一个很好的机会，但是我觉得我发挥得很不好，队友在比赛中表现的非常出色，对两位队友表示歉意，并且我会引以为戒，在以后训练中好好努力，争取在下次比赛中达到最好的状态！

posted @ 2010-10-04 09:58 wujiawei 阅读(298) | 评论 (0) | 编辑收藏

2010年9月7日 #

【转载】 ZJU2004 Commedia dell'arte 八数码问题有解的条件及其推广

ZJU2004 Commedia dell'arte 八数码问题有解的条件及其推广
转自http://blog.csdn.net/tiaotiaoyly/archive/2008/01/01/2008233.aspx

题目描述：

此题是经典的八数码问题的推广。一个M×M×M的立方体，原始状态一次给方块编号1 ~ M^3-1，最后一个格子空缺。现在给定任意一个方块的排列，问能否通过合法变换回到原始状态。

解题思路：

题目要求一个三维空间的N数码问题，问是否有解。我们先从简单的情况考虑。

>从八数码问题入手

我们首先从经典的八数码问题入手，即对于八数码问题的任意一个排列是否有解？有解的条件是什么？

我在网上搜了半天，找到一个十分简洁的结论。八数码问题原始状态如下：

1 2 3
4 5 6
7 8

为了方便讨论，我们把它写成一维的形式，并以0代替空格位置。那么表示如下：

1 2 3 4 5 6 7 8 0

通过实验得知，以下状态是无解的（交换了前两个数字1 2）：

2 1 3 4 5 6 7 8 0

八数码问题的有解无解的结论：

一个状态表示成一维的形式，求出除0之外所有数字的逆序数之和，也就是每个数字前面比它大的数字的个数的和，称为这个状态的逆序。

若两个状态的逆序奇偶性相同，则可相互到达，否则不可相互到达。

由于原始状态的逆序为0（偶数），则逆序为偶数的状态有解。

也就是说，逆序的奇偶将所有的状态分为了两个等价类，同一个等价类中的状态都可相互到达。

简要说明一下：当左右移动空格时，逆序不变。当上下移动空格时，相当于将一个数字向前（或向后）移动两格，跳过的这两个数字要么都比它大（小），逆序可能±2；要么一个较大一个较小，逆序不变。所以可得结论：只要是相互可达的两个状态，它们的逆序奇偶性相同。我想半天只能说明这个结论的必要性，详细的证明请参考后面的附件。

>推广二维N×N的棋盘

我们先来看看4×4的情况，同样的思路，我们考虑移动空格时逆序的变化情况。

1 2    3 4
5   6 7    8
9    A    B   C
D   E    F

我们用字母A~F代替数字10~15。同样地，当左右移动的时候，状态的逆序不改变。而当上下移动的时候，相当于一个数字跨过了另外三个格子，它的逆序可能±3或±1，逆序的奇偶性必然改变。那么又该如何

1 2    3 4
5   6 7    8
9    A    B
C   D   E    F

可以证明，以上状态是一个无解的状态（将C移到了第四行）。该状态的逆序为0，和原始状态相同，但是它的空格位置在第三行。若将空格移到第四行，必然使得它的逆序±1或±3，奇偶性必然改变。所以它是一个无解的状态。

然而以下状态就是一个有解的状态（交换了前两个数字1 2）：

2    1    3 4
5   6 7    8
9    A    B
C   D   E    F

这个状态的逆序为1，和原始状态奇偶性不同，而空格位置在第三行。由于空格每从第三行移动到第四行，奇偶性改变。则该状态的可到达原始状态。

通过观察，得出以下结论：

N×N的棋盘，N为奇数时，与八数码问题相同。

N为偶数时，空格每上下移动一次，奇偶性改变。称空格位置所在的行到目标空格所在的行步数为空格的距离（不计左右距离），若两个状态的可相互到达，则有，两个状态的逆序奇偶性相同且空格距离为偶数，或者，逆序奇偶性不同且空格距离为奇数数。否则不能。

也就是说，当此表达式成立时，两个状态可相互到达：(状态1奇偶性==状态2奇偶性)==(空格距离%2==0)。

此结论只是由观察得知的，但是还没证明过，请高手指点。

另外再详细说明一下，无论N是奇数还是偶数，空格上下移动，相当于跨过N-1个格子。那么逆序的改变可能为一下值±N-1，±N-3，±N-5 …… ±N-2k-1。当N为奇数数时N-1为偶数，逆序改变可能为0；当N为偶数时N-1为奇数，逆序的改变不能为0，只能是奇数，所以没上下移动一次奇偶性必然改变。

>推广到三维N×N×N

其实，三维的结论和二维的结论是一样的。

考虑左右移动空格，逆序不变；同一层上下移动空格，跨过N-1个格子；上下层移动空格，跨过N^2-1个格子。

当N为奇数时，N-1和N^2-1均为偶数，也就是任意移动空格逆序奇偶性不变。那么逆序奇偶性相同的两个状态可相互到达。

当N为偶数时，N-1和N^2-1均为奇数，也就是令空格位置到目标状态空格位置的y z方向的距离之和，称为空格距离。若空格距离为偶数，两个逆序奇偶性相同的状态可相互到达；若空格距离为奇数，两个逆序奇偶性不同的状态可相互到达。

讨论到这里，题目问题也就解决了

参考资料：

水木清华BBS精华区：关于八码数问题有解与无解的证明 http://www.cnw3.org/smth/AI/5/8/00000001.htm
豆瓣网BBS ：http://www.douban.com/group/topic/1724083/

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

附： 关于八码数问题有解与无解的证明

转载自【水木清华BBS精华区】：http://www.cnw3.org/smth/AI/5/8/00000001.htm

< language="javascript" src="http://www.pku.biz/top.js" type="text/javascript">

发信人: YourMajesty (花痴~~~~小魔男), 信区: AI
标  题: 关于八码数问题有解与无解的证明(zz)
发信站: BBS 水木清华站 (Fri Nov 23 22:26:49 2001)

    8数码难题搜索时，有时候是无解的，8数码问题总共有9!种状态，如果用计算机一
个一个去搜索去判断哪些有解哪些误解，无疑要花费很长的时间，也没必要。作为一种
智力游戏，玩之余，我在想，能否通过事先的分析来判断哪些问题有解，哪些问题无解
呢？对于有解的问题，是否能通过一种固定的步骤来得到解？经过昨天晚上和今天的仔
细分析，我觉得我已经得到了这个问题的初步解答，下面我公布一下我得到的结果和证
明，抛砖引玉，如果大家发现其中有什么问题，欢迎来我宿舍一起讨论或者给我发Emai
l。

我的证明分好几个步骤，恳请大家能够耐心的看下去，我会尽量说得简洁一点。

    一、我的结论
    我们将九宫格按行排成一行共九个数(空格也占一个位置，在本文种，我用@表示空
格)。比如：    1 2 3     4 @ 5     ＝>   1 2 3 4 @ 5 6 7 8    6 7 8     这样
，九宫格的每一种状态和上图的行之间是一一对应的。在代数上册我们学过逆序的概念
，也就是对于任意一对数，如果前面的数比后面的数大，则为一对逆序。对于一个序列
，我们定义其逆序奇偶性如下：    如果其中有奇数对逆序，称之逆序奇；如果其中有
偶数对逆序，称之为逆序偶。这样，对于1，2，...，n这n个数，其所有的排列可以分为
两类，逆序奇类和逆序偶类。相对应的，九宫图(除去空格)也有它的奇偶性，我们的定
理是：
    所有的奇九宫图之间是可达的，所有的偶九宫图之间也是可达的，但奇九宫图和偶
九宫图之间互不可达。

二、问题的转化
为了证明上述定理，我想先对问题进行一下转化。我定义两种行序列的变换：一种
是空格@和相邻的数对换，一种是空格@和前后隔两个数的数之间的对换，前者对应着空
格在九宫图中的左右移动，后者对应着空格在九宫图中的上下移动。

引理一：在上述的两种对换下，序列的奇偶性不改变。这个引理很容易证明。
首先，相邻的对换肯定不改变奇偶性；其次，隔两格的对换也不改变奇偶性，它相当于
三个数的轮换，我们可以自己列举一下几种情况验证一下。这就说明了奇九宫图和偶九
宫图之间是互不可达的。

    引理二：转化后行序列在上面定义的两种对换下的任意操作，可以转换成九宫图中
空格的合法变化。    这个引理也是比较容易证明的。我们只要证明如下的几种状态之
间是互达的：    a b c        a b @        a b c        a b c    @ d e  <=>
c d e        d e f  <=>   d e @    f g h        f g h        @ g h        f
g h    通过计算机搜索，可以发现上面两对状态之间的确是互达的。从而，我们可以
假定上面两种状态之间的转换可以用行序列中的两种邻对换来代替。
    想提一点的是，九宫图之间的变换是可逆的。下面，到了问题的核心部分了。

    引理三：所有的奇状态可以转换为 @ 1 2 3 4 5 6 7 8, 所有的偶状态
可以转换为 @ 2 1 3 4 5 6 7 8.    要证明这个引理，得分几个步骤。我的想法是先设
法把8移到最后一个，然后8保持不动(注意，我们这里的不动只是形式上不动，但不管怎
样，我们的每一个变换后，8还是保持在最后一个，余类似)，再将7移到8之前，然后，
保持7和8不动，依次移动6，5，4，3，得到 * * * 3 4 5 6 7 8这里 * * *是 @ 1 2 的
一个排列。到这里，我想要得到前面的两种状态之一是显然的了。下面，我说明，上面
的想法是可以实现的。如下：

   1. 对于 a b c @ ，我们可以将其中的任意一个移到
最后，并且对变换仅限于这四个位置上。显然，对于a，c是一步就可以做到的。对于b，
步骤如下：   a b c @ -> @ b c a -> b @ c a -> b c @ a -> b c a @ -> @ c a b
   2. 先把要移到最后位置的那个数移到最后四个位置之一，然后再将空格移到最后一
个位置，用1的方法将待移动的数变换到最后一个位置。循环这样做即可。    引理三证
毕。

证完了这三个引理，定理的成立就是显然的了。首先，将奇偶性相同的两种状态都
变换到上述两种标准状态之一，然后对其一去逆变换即可。以上是我的所有证明，有些
地方在计算机上写起来不是太清楚。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

posted @ 2010-09-07 08:51 wujiawei 阅读(710) | 评论 (0) | 编辑收藏

2010年9月1日 #

[转]Java图形界面编程

Java图形界面编程

AWT

AWT(Abstract Window Toolkit)，抽象窗口工具包，SUN公司提供的用于图形界面编程(GUI)的类库。基本的AWT库处理用户界面元素的方法是把这些元素的创建和行为委托给每个目标平台上（Windows、Unix、Macintosh等）的本地GUI工具进行处理。例如：如果我们使用AWT在一个Java窗口中放置一个按钮，那么实际上使用的是一个具有本地外观和感觉的按钮。这样，从理论上来说，我们所编写的图形界面程序能运行在任何平台上，做到了图形界面程序的跨平台运行。

布局管理器

1）容器里组件的位置和大小是由布局管理器来决定的。容器对布局管理器的特定实例保持一个引用。当容器需要定位一个组件时，它将调用布局管理器来完成。当决定一个组件的大小时，也是如此。

2）在AWT中，给我们提供了五种布局管理器：

BorderLayout、FlowLayout、GridLayout、CardLayout、GridBagLayout

AWT事件模型

1） Events(事件)：描述发生了什么的对象。

2） Event source(事件源)：事件的产生器。

3） Event handlers(事件处理器)：接收事件对象、解释事件对象并处理用户交互的方法。

事件监听器

实现了监听器接口的类。一个监听器对象是一个实现了专门的监听器接口的类的实例。

如增加窗口监听，实现按关闭按钮时退出，WindowAdapter为一个空实现了WindowListener接口的抽象类，故其不能直接用new来创建对象，可以通过匿名类来实现，在中间重写windowClosing方法：

addWindowListener(new WindowAdapter()

       {

           public void windowClosing(WindowEvent e)

           {

              System.exit(0);

           }

       });

如对按钮增加单击事件监听：当点击按钮Welcome时，将显示为Hello。

     Button btn1=new Button("Welcome");

btn1.addActionListener(new ActionListener()

       {

           public void actionPerformed(ActionEvent e)

           {

              ((Button)e.getSource()).setLabel("Hello");

           }

       });

对于CardLayout布局管理器，可以通过增加事件监听器来实现卡片式翻动：

Panel cardPanel=new Panel();



       Button btn1=new Button("North");

       Button btn2=new Button("South");



       final CardLayout cl=new CardLayout();

       cardPanel.setLayout(cl);

       ActionListener al=new ActionListener()

       {

        public void actionPerformed(ActionEvent e)

       {

           cl.next(cardPanel);

       }

       };

       btn1.addActionListener(al);

       btn2.addActionListener(al);



       cardPanel.add(btn1,"1");

       cardPanel.add(btn2,"2");

菜单及打开、保存对话框

先创建菜单栏MenuBar，在创建菜单Menu，最后创建菜单项MenuItem，然后把菜单项加到菜单上，把菜单加到菜单栏上，最后用setMenuBar把菜单栏加到Frame上。

为打开菜单项增加事件监听器，创建打开文件对话框，然后通过TextArea来显示打开的文件内容。

final Frame f=new Frame("MenuBarTest");

       f.setSize(600,400);

       f.setLocation(100,100);

MenuBar mb=new MenuBar();

       Menu mn1=new Menu("File");

       Menu mn2=new Menu("Edit");

       MenuItem m1=new MenuItem("new");

       MenuItem m2=new MenuItem("open");

       MenuItem m3=new MenuItem("save");

       MenuItem m4=new MenuItem("exit");

MenuItem m5=new MenuItem("copy");

       MenuItem m6=new MenuItem("paste");



       final TextArea ta=new TextArea();

       f.add(ta);

m2.addActionListener(new ActionListener()

       {

           public void actionPerformed(ActionEvent e)

           {

              FileDialog fd=new FileDialog(f,"打开文件对话框",FileDialog.LOAD);

              fd.show();

                 // getDirectory()获得对话框打开目录的路径，str即打开文件的完整路径

              String str=fd.getDirectory()+fd.getFile();

           if(str!=null)

           {

              try

             {

              FileInputStream fis=new FileInputStream(str);

                 byte []buf=new byte[10*1024];

                 int len=fis.read(buf);

                 ta.append(new String(buf,0,len));

                 fis.close();

              }

              catch(Exception ex)

              {

                  ex.printStackTrace();

              } } }

       });



       m3.addActionListener(new ActionListener()

       {

           public void actionPerformed(ActionEvent e)

           {

              FileDialog fd=new FileDialog(f,"保存文件对话框",FileDialog.SAVE);

              fd.show();

           }

       });



       m4.addActionListener(new ActionListener()

       {

           public void actionPerformed(ActionEvent e)

           {

              System.exit(0);

           }

       });



       mn1.add(m1);

       mn1.add(m2);

       mn1.add(m3);

       mn1.add(m4);

       mn2.add(m5);

       mn2.add(m6);

       mb.add(mn1);

       mb.add(mn2);

       f.setMenuBar(mb);

       f.show();

posted @ 2010-09-01 08:46 wujiawei 阅读(239) | 评论 (0) | 编辑收藏

2010年8月24日 #

两个几何 ZOJ 3376 && ZOJ 3379

ZOJ 3376 Safest Points

题目大意：给平面上一些点，以及从这点出发的射线的方向。对于平面上的整点，

首先定义危险的点为平面上距离射线曼哈顿距离小于1的整点。要求求出距离危险点最远的整点的坐标，若有多个则按字典序排序。

我的做法：首先要注意距离射线曼哈顿距离小于1的可以这样判断，即判断射线与整点区间的交点，若在整点之间就说明这周围的顶点都是危险点，例：

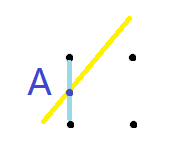
其中A点上下两个点就为危险点，只需求出根据x坐标递增或递减，

根据射线的方程求A点的纵坐标，分别取上整和下整，然后将这些点标记为危险点。再以y坐标递增或递减，对x采取同样的做法，标记危险点，这样的两次是为了保证边界的情况。

求出所有危险点之后，进行一次BFS就可以得到答案。

总结：开始错在边界上了，要考虑到起点不在整点上以及注意dx，dy方向

ZOJ 3379 Master Spark

题目大意：给出以原点为顶点的抛物线，平面上有若干点，求出一个角度能打到的点最多，输出这个数目。

我的做法：对每个点判断抛物线旋转到什么极角时能打得到，就是每个点对应的抛物线的极角区间，然后统计哪个极角区间覆盖次数最多即可。

这两道题都是浙大月赛的题，有事没做，后来队友说有两道几何让我做。。- -|||觉得题目很好的，前面那个题一开始就想的差不多，后来敲完发现问题改完就过了，后面那个倒是卡了好久，主要是极角上的问题，按区间左右分开处理加标记就不对，改成按区间两端点存就不对，不知道为啥，大概是精度的问题吧，以后注意吧哈哈，加油！

posted @ 2010-08-24 19:52 wujiawei 阅读(320) | 评论 (0) | 编辑收藏

2010年8月23日 #

Something about the matrix

摘要: Something about the matrix HOJ 2255 Not Fibonacci 题目大意：给出一个类似于Fibonacci的递推关系式f(n) = p * f(n-1) + q * f(n - 2).求出我的做法：根据S(n)和f(n)的递推来构造一个5阶的矩阵： &n... 阅读全文

posted @ 2010-08-23 10:22 wujiawei 阅读(222) | 评论 (0) | 编辑收藏

2010年8月21日 #

单位圆覆盖平面上点

摘要: HOJ 2704 Phone Cell 题目大意：给定圆的半径，以及平面上的一些点的坐标，问用此半径的圆最多可覆盖平面上多少点我的做法：首先枚举一个圆与其他圆的相交情况，记录两圆相交的弧，也就是记录两个交点对于圆心的极角，并且作上标记，进入的点为+1，退出的点为-1。那么对于每个圆可以得到若干个极角的区间，所以排序之后再扫描一遍，遇到进入的点计数器+1，遇到退出的计数器-1，每次都动态更新最... 阅读全文

posted @ 2010-08-21 14:17 wujiawei 阅读(885) | 评论 (0) | 编辑收藏

【转】 POJ计算几何

计算几何题的特点与做题要领：
1.大部分不会很难，少部分题目思路很巧妙
2.做计算几何题目，模板很重要，模板必须高度可靠。
3.要注意代码的组织，因为计算几何的题目很容易上两百行代码，里面大部分是模板。如果代码一片混乱，那么会严重影响做题正确率。
4.注意精度控制。
5.能用整数的地方尽量用整数，要想到扩大数据的方法（扩大一倍，或扩大sqrt2）。因为整数不用考虑浮点误差，而且运算比浮点快。

一。点，线，面，形基本关系，点积叉积的理解

POJ 2318 TOYS（推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=2318
POJ 2398 Toy Storage（推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=2398
一个矩形，有被若干直线分成N个格子，给出一个点的坐标，问你该点位于哪个点中。
知识点：其实就是点在凸四边形内的判断，若利用叉积的性质，可以二分求解。

POJ 3304 Segments
http://acm.pku.edu.cn/JudgeOnline/problem?id=3304
知识点：线段与直线相交，注意枚举时重合点的处理

POJ 1269 Intersecting Lines
http://acm.pku.edu.cn/JudgeOnline/problem?id=1269
知识点：直线相交判断，求相交交点

POJ 1556 The Doors （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=1556
知识点：简单图论＋简单计算几何，先求线段相交，然后再用Dij求最短路。

POJ 2653 Pick-up sticks
http://acm.pku.edu.cn/JudgeOnline/problem?id=2653
知识点：还是线段相交判断

POJ 1066 Treasure Hunt
http://acm.pku.edu.cn/JudgeOnline/problem?id=1066
知识点：线段相交判断，不过必须先理解“走最少的门”是怎么一回事。

POJ 1410 Intersection
http://acm.pku.edu.cn/JudgeOnline/problem?id=1410
知识点：线段与矩形相交。正确理解题意中相交的定义。
详见：http://hi.baidu.com/novosbirsk/blog/item/68c682c67e8d1f1d9d163df0.html

POJ 1696 Space Ant （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=1696
德黑兰赛区的好题目。需要理解点积叉积的性质

POJ 3347 Kadj Squares
http://acm.pku.edu.cn/JudgeOnline/problem?id=3347
本人的方法极度猥琐。复杂的线段相交问题。这个题目是计算几何的扩大数据运算的典型应用，扩大根号2倍之后就避免了小数。

POJ 2826 An Easy Problem?! （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=2826
问：两条直线组成一个图形，能容纳多少雨水。很不简单的Easy Problem，要考虑所有情况。你不看discuss看看能否AC。（本人基本不能）提示一下，水是从天空垂直落下的。

POJ 1039 Pipe
http://acm.pku.edu.cn/JudgeOnline/problem?id=1039
又是线段与直线相交的判断，再加上枚举的思想即可。

POJ 3449 Geometric Shapes
http://acm.pku.edu.cn/JudgeOnline/problem?id=3449
判断几何体是否相交，不过输入输出很恶心。
此外，还有一个知识点，就是给出一个正方形（边不与轴平行）的两个对角线上的顶点，需要你求出另外两个点。必须掌握其方法。

POJ 1584 A Round Peg in a Ground Hole
http://acm.pku.edu.cn/JudgeOnline/problem?id=1584
知识点：点到直线距离，圆与多边形相交，多边形是否为凸

POJ 2074 Line of Sight （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=2074
与视线问题的解法，关键是求过两点的直线方程，以及直线与线段的交点。数据有一个trick，要小心。

二。凸包问题

POJ 1113 Wall
http://acm.pku.edu.cn/JudgeOnline/problem?id=1113
知识点：赤裸裸的凸包问题，凸包周长加上圆周。

POJ 2007 Scrambled Polygon
http://acm.pku.edu.cn/JudgeOnline/problem?id=2007
知识点：凸包，按极角序输出方案

POJ 1873 The Fortified Forest （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=1873
World Final的水题，先求凸包，然后再搜索。由于规模不大，可以使用位运算枚举。
详见：http://hi.baidu.com/novosbirsk/blog/item/333abd54c7f22c52574e0067.html

POJ 1228 Grandpa's Estate （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=1228
求凸包顶点数目，很多人求凸包的模板是会多出点的，虽然求面积时能得到正确答案，但是在这个题目就会出问题。此外，还要正确理解凸包的性质。

POJ 3348 Cows
http://acm.pku.edu.cn/JudgeOnline/problem?id=3348
凸包面积计算

三。面积问题，公式问题

POJ 1654 Area
http://acm.pku.edu.cn/JudgeOnline/problem?id=1654
知识点：利用有向面积（叉积）计算多边形面积

POJ 1265 Area
http://acm.pku.edu.cn/JudgeOnline/problem?id=1265
POJ 2954 Triangle
http://acm.pku.edu.cn/JudgeOnline/problem?id=2954
Pick公式的应用，多边形与整点的关系。（存在一个GCD的关系）

四。半平面交

半平面交的主要应用是判断多边形是否存在核，还可以解决一些与线性方程组可行区域相关的问题（就是高中时的那些）。

POJ 3335 Rotating Scoreboard
http://acm.pku.edu.cn/JudgeOnline/problem?id=3335
POJ 3130 How I Mathematician Wonder What You Are!
http://acm.pku.edu.cn/JudgeOnline/problem?id=3130
POJ 1474 Video Surveillance
http://acm.pku.edu.cn/JudgeOnline/problem?id=1474
知识点：半平面交求多边形的核，存在性判断

POJ 1279 Art Gallery
http://acm.pku.edu.cn/JudgeOnline/problem?id=1279
半平面交求多边形的核，求核的面积

POJ 3525 Most Distant Point from the Sea （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=3525
给出一个多边形，求里面的一个点，其距离离多边形的边界最远，也就是多边形中最大半径圆。
可以使用半平面交+二分法解。二分这个距离，边向内逼近，直到达到精度。

POJ 3384 Feng Shui （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=3384
半平面交实际应用，用两个圆覆盖一个多边形，问最多能覆盖多边形的面积。
解法：用半平面交将多边形的每条边一起向“内”推进R，得到新的多边形，然后求多边形的最远两点。

POJ 1755 Triathlon （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=1755
半平面交判断不等式是否有解。注意不等式在转化时正负号的选择，这直接影响到半平面交的方向。

POJ 2540 Hotter Colder
http://acm.pku.edu.cn/JudgeOnline/problem?id=2540
半平面交求线性规划可行区域的面积。

POJ 2451 Uyuw's Concert
http://acm.pku.edu.cn/JudgeOnline/problem?id=2451
Zzy专为他那篇nlogn算法解决半平面交问题的论文而出的题目。

五。计算几何背景，实际上解题的关键是其他问题（数据结构、组合数学，或者是枚举思想）
若干道经典的离散化＋扫描线的题目，ACM选手必做题目

POJ 1151 Atlantis （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=1151
POJ 1389 Area of Simple Polygons
http://acm.pku.edu.cn/JudgeOnline/problem?id=1389
矩形离散化，线段树处理，矩形面积求交

POJ 1177 Picture （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=1177
矩形离散化，线段树处理，矩形交的周长，这个题目的数据比较强。线段树必须高效。

POJ 3565 Ants （推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=3565
计算几何中的调整思想，有点像排序。要用到线段相交的判断。
详见：http://hi.baidu.com/novosbirsk/blog/item/fb668cf0f362bec47931aae2.html

POJ 3695 Rectangles
http://acm.pku.edu.cn/JudgeOnline/problem?id=3695
又是矩形交的面积，但是由于是多次查询，而且矩形不多，使用组合数学中的容斥原理解决之最适合。线段树是通法，但是除了线段树，还有其他可行的方法。

POJ 2002 Squares
http://acm.pku.edu.cn/JudgeOnline/problem?id=2002
枚举思想，求平面上若干个点最多能组成多少个正方形，点的Hash

POJ 1434 Fill the Cisterns!（推荐）
http://acm.pku.edu.cn/JudgeOnline/problem?id=1434
一开始发昏了，准备弄个线段树。其实只是个简单的二分。

六。随机算法
POJ 2420 A Star not a Tree?
http://acm.pku.edu.cn/JudgeOnline/problem?id=2420
多边形的费马点。所谓费马点，就是多边形中一个点P，该点到其他点的距离之和最短。四边形以上的多边形没有公式求费马点，因此可以使用随机化变步长贪心法。
详见：http://hi.baidu.com/novosbirsk/blog/item/75983f138499f825dd54019b.html

七。解析几何
这种题目本人不擅长，所以做得不多，模板很重要。当然，熟练运用叉积、点积的性质还是很有用的。
POJ 1375 Intervals
http://acm.pku.edu.cn/JudgeOnline/problem?id=1375
知识点：过圆外一点求与圆的切线

POJ 1329 Circle Through Three Points
http://acm.pku.edu.cn/JudgeOnline/problem?id=1329
求三角形外接圆

POJ 2354 Titanic
http://acm.pku.edu.cn/JudgeOnline/problem?id=2354
求球面上两个点的距离，而且给的是地理经纬坐标。

POJ 1106 Transmitters
http://acm.pku.edu.cn/JudgeOnline/problem?id=1106
角度排序，知道斜率求角度，使用atan函数。

POJ 1673 EXOCENTER OF A TRIANGLE
http://acm.pku.edu.cn/JudgeOnline/problem?id=1673
可以转化为三角形的垂心问题。

八。旋转卡壳

POJ 2187 Beauty Contest
http://acm.pku.edu.cn/JudgeOnline/problem?id=2187
凸包求最远点对。可以暴力枚举，也可以使用旋转卡壳。

POJ 3608 Bridge Across Islands（难）
http://acm.pku.edu.cn/JudgeOnline/problem?id=3608
两个凸包的最近距离。本人的卡壳始终WA。郁闷。

九。其他问题
POJ 1981 Circle and Points
http://acm.pku.edu.cn/JudgeOnline/problem?id=1981
求单位圆最多能覆盖平面上多少个点

本文来自CSDN博客，转载请标明出处：http://blog.csdn.net/tyger/archive/2009/08/25/4480029.aspx

posted @ 2010-08-21 11:11 wujiawei 阅读(871) | 评论 (0) | 编辑收藏

2010年8月20日 #

多校2010 Multi-University Training Contest(12)

2010 Multi-University Training Contest(12)

比赛中只做了那个关于圆的几何题，其他的都是队友做的。

How many times

题目大意：给平面上一些圆，求出覆盖次数最多的区域，输出次数。

我的做法：因为题目中说圆数目最多100个，所以我先将每两个圆的交点求出存起来，然后对每一个交点判断它在多少圆中，那么就可以得到这个点所在区域的覆盖最大次数，因为交点是各个区域交集的边缘。

然后对于不相交的情况：

枚举每个圆，统计有多少圆完全在它里面，取一个最大值，然后与上面相交情况比较取最大值，两者不会冲突，因为对交点处理的时候判断的是在圆内，那就把包含的加上了。

总结：比赛时候遇到两个问题：一开始我提问一个点算不算一个被统计的区域，回答说“No，it’s just a point.”我就把一开始的做法（上面的那个）换掉了，开始往扫描线上面考虑，后来也不对，发现过的人越来越多，看了一下提问区，有人问同样的问题，居然回答是“Yes”。。囧。。。于是按原来的想法写，交了WA。。后来一番折磨之后队友突然出了一组数据，卡掉了。。原来是内含的情况不等式只写了一半，另一半没判断出来。。以后要认真啊！

赛后做的题：

Frost Chain

题目大意：给出5个英雄的位置，以及初始血量，现在有一个技能，初始打到每个英雄是等概率的，而且打到的话损失一点体力，接下来这个技能会继续弹到别的英雄那，一直下去直到次数的上限，每次它能弹到的英雄必须在一个距离范围内，而且对他们每个人都是等概率的。现在问题是求出每个英雄死的概率。

我的做法：用一个八维数组：dp[a][b][c][d][e][now][nowd][turn]

表示当前五个人体力依次是a、b、c、d、e，而且当前技能在now这个人身上，第turn次，nowd这个英雄死亡的概率，然后按照条件记忆化搜索就可以了。

总结：DP是我的弱项，dota更不会，所以这题对我来说是挑战。。。

Easy Geometry

题目大意：给出平面上的一些点，以及选择它们的概率，求出这些点构成的凸包的点数的期望。

我的做法：看了解题报告，想了一阵，问了luzilon学长，然后才明白。问题可以转化为求每个点出现在凸包上的概率的和。

每个点出现在凸包上的概率可以这样做：对每一个顶点，让其他顶点对该顶点进行极角排序，然后枚举剩下点作为该顶点在凸包中的邻接点，那么这样就有了凸包中的一条边了，这个点在凸包上的概率等价于这条边在凸包上的概率，也就是要将点集从被选的邻接点开始按照极角序扫描，180度以内的全都不选的概率就是这条边作为凸包边的概率（凸包的性质），这样每次只算半边，防止后面计算的重复。最后还要加上全不选的概率，只有一个自己这点。

总结：觉得是很好的一道题。学到不少，思路很好啊这题。

posted @ 2010-08-20 11:29 wujiawei 阅读(275) | 评论 (0) | 编辑收藏

2010年8月18日 #

Rabin Karp 算法

摘要: 部分转载Rabin-Karp算法Rabin-Karp算法是由Rabin和Karp提出的一个在实际中有比较好应用的字符串匹配算法，此算法的预处理时间为O(m)，但它的在最坏情况下的时间复杂度为O((2n-m+1)m)，而平均复杂度接近O(m+n)，此算法的主要思想就是通过对字符串进行哈稀运算，使得算法可以容易的派出大量的不相同的字符串，假设模式字符串的长度为m，利用Horner法则p = p[m]... 阅读全文

posted @ 2010-08-18 08:34 wujiawei 阅读(452) | 评论 (0) | 编辑收藏

转载自某百度空间 “素数分解为平方和 ”

素数分解为平方和

定理：设p是素数，则p是两个数的平方和，当且仅当p≡1 (mod 4)或p=2。

要由p≡1 (mod 4)推出p是两个数的平方和需要使用费马的无限下降算法：设p≡1 (mod 4)，目的是找出A²+B²=p的一组解。

1 先找出一组可行解满足A²+B²=Mp，其中M<p。可以让A取x²≡-1 (mod p)的某个解，B取1。任取一个数1<a<p，计算A≡a^(p-1)/4 (mod p)，则由24章的定理可知A²≡a^(p-1)/2≡(a/p) (mod p)，即A²不是1就是-1，而且概率都是50%。多取几次a，必定能找到A²≡-1 (mod p)的解。

2 计算u≡A,v≡B，且-0.5M<=u,v<=0.5M的u和v。

3 由于u²+v²≡A²+B²≡0 (mod M)，可设u²+v²=Mr（1<=r<M）。

4 相乘，即(u²+v²)(A²+B²)=M²rp。

5 上式可化为(uA+vB)²+(vA-uB)²=M²rp。

6 左右都除以M²，得

((uA+vB)/M)²+((vA-uB)/M)²=rp。

可以证明M|uA+vB且M|vA-uB。

7 若r=1，则算法结束，否则转2.

算法每次都维护一组可行解A²+B²=Mp，且每次执行都使得M单调递减。实际上，可以证明r<=M/2，即系数至少会折半，因此总的运行次数是log级的。

对于任意整数a,如果a=p₁p₂，且p_1,p₂都是符合上一章中分解条件的素数。设p₁=u²+v²,p₂=A²+B²，则

a= (u²+v²)(A²+B²)=(uA+vB)²+(vA-uB)²

换句话说，只要a分解质因数后所有的因子都是可分解的素数，则a可分解为两个整数的平方和。

定理：(a) 设m是正整数，且m=p₁p₂…p_r，其中p₁…p_r互不相同。则m可分解为两个整数的平方和当且仅当所有的p_i≡1 (mod 4)或等于2。

(b) m可写成m=a²+b² (其中gcd(a,b)=1)当且仅当它满足下列条件之一：

(i) m是奇数且任何m的素因数模4余1

(ii) m是偶数，m/2满足(i)。

再考虑一下勾股数，可以得出结论：

一个数c是一组本原勾股数中最大的数，当且仅当c的素因数都模4余1。

posted @ 2010-08-18 08:34 wujiawei 阅读(339) | 评论 (0) | 编辑收藏

仅列出标题

导航

留言簿

随笔档案

阅读排行榜

评论排行榜

常用链接

统计

最新评论