经典的压缩DP.
题目描述:
Bugs公司生产一种2x3单位尺寸的高科技芯片，芯片被嵌入NxM的模板内。模板接受过严格的检查，损坏的单位小方格已被标上黑色记号。
嵌入芯片的要求是，放置芯片的区域内不能有黑色记号，芯片间不能重叠。 求出可能的最大芯片数量。
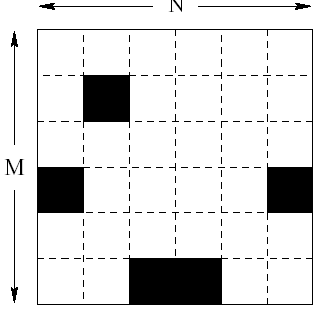
分析：
我们从左至右考虑每列的放置。由于芯片长度只有3，所以第j列芯片的放置只受第j-1和j-2列放置情况的影响。同时，如果方格(i,j-1)被黑色标记或其他芯片占据，方格(i,j-2)即使空闲对第j列也没影响。
这里以0表示方格(i,j-2),(i,j-1)空闲； 以1表示方格(i,j-2)被占据,方格(i,j-1)空闲；以2表示方格(i,j-1)被占据。对于每一行有三种可能的状态。所以第j-2和j-1列的放置情况可以用m位的3进制表示。
状态转移方程推导：
假如我们现在要放置第j列，那么它将受到前两列放置情况的影响。那么我们怎么来表示状态转移呢？
令f[i][j]前j列放置好后，并且放置情况为i时芯片的最大数量。f[i][j]=max{f[k][j-1]+num}. 由此,第j列的放置可由前j-1列的放置情况来推导。
详细见代码：
#include<iostream>
using namespace std;
int n,m,t;
bool bug[12][155];
int f[60000][2];
int b[12],s[12];
void dfs(int j,int i,int cur,int sta,int num)
{
int tt,d;
if(cur>m)
{
if(f[sta][j&1]<f[i][(j-1)&1]+num)
f[sta][j&1]=f[i][(j-1)&1]+num;
return;
}
//当前位置不放芯片.
if(bug[cur][j]) tt=2;
else if(s[cur]>0) tt=s[cur]-1;
else tt=0;
d=sta+tt*b[cur-1];
dfs(j,i,cur+1,d,num);
//横着放芯片.
if(cur+1<=m&&s[cur]==0&&s[cur+1]==0&&!bug[cur][j]&&!bug[cur+1][j])
{
d=sta+2*b[cur-1]+2*b[cur];
dfs(j,i,cur+2,d,num+1);
}
//竖着放芯片.
if(cur+2<=m&&s[cur]<=1&&s[cur+1]<=1&&s[cur+2]<=1&&!bug[cur][j]&&!bug[cur+1][j]&&!bug[cur+2][j])
{
d=sta+2*b[cur-1]+2*b[cur]+2*b[cur+1];
dfs(j,i,cur+3,d,num+1);
}
}
int main()
{
int i,j,k,v;
b[0]=1;
for(i=1;i<=10;i++)
b[i]=b[i-1]*3;
scanf("%d",&t);
while(t--)
{
int x,y;
scanf("%d%d%d",&n,&m,&k);
memset(bug,false,sizeof(bug));
for(i=0;i<k;i++)
{
scanf("%d%d",&x,&y);
bug[y][x]=true;
}
memset(f,-1,sizeof(f));
f[b[m]-1][0]=0;
for(j=1;j<=n;j++)
{
for(i=0;i<b[m];i++) f[i][j&1]=-1;
for(i=0;i<b[m];i++)
if(f[i][(j-1)&1]!=-1)
{
v=i;
s[0]=1;
for(k=1;k<=m;k++)
{
s[k]=v%3;
v/=3;
}
dfs(j,i,1,0,0);
}
}
int ans=-1;
for(i=0;i<b[m];i++)
if(ans<f[i][n&1]) ans=f[i][n&1];
printf("%d\n",ans);
}
return 0;
}posted on 2010-08-15 13:09
wuxu 阅读(288)
评论(0) 编辑 收藏 引用 所属分类:
动态规划