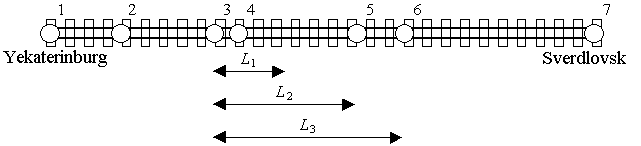
现在有一条“叶卡特琳堡-斯维尔德洛夫斯克”铁路线。它有若干个火车站。这个铁路线可以用一条线段来表示,而火车站就是线段上的点。铁路起始于叶卡特琳堡(Eakterinburg),终止于斯维尔德洛夫斯克(Sverlovsk),且各站从叶卡特琳堡(它的编号是1)至斯维尔德洛夫斯克(终点)编号。
| distance X between stations |
price for the ticket |
| 0 < X ≤ L1 |
C1 |
| L1 < X ≤ L2 |
C2 |
| L2 < X ≤ L3 |
C3 |
当且仅当两站间距离不大于L3时才能购买这两站之间的直达车票。所以有时须要购买若干张票来完成整个旅行。
例如,在上图,整条铁路有七个站。从第2站不能直达第6站(因为距离大于L3),但有另外几种方法购票。其中一种是买两张票:一张是从第2站至第3站(票价为C2),另一张是从第3站至第6站(票价为C3),注意,虽然从第2站至第6站的距离为2×L2,但不可以买两张价值C2的票,因为一张票只可以用一次且起点和终点必须在车站上。
你的任务时计算给出的两站之间的最小花费。
input:
输入的第一行包含六个由空格隔开的整数L1,L2,L3,C1,C2,C3(1<=L1<L2<L3<=10^9,1<=C1<C2<C3<=10^9)。第二行为车站数N(2<=N<=10000)。第三行有两个由空格隔开的不等的整数,表示旅行起点和终点。接下来的N-1行为起点(叶卡特琳堡)至其它站的距离。这些距离为互不相等的正整数而且呈上升序列。从叶卡特琳堡至斯维尔德洛夫斯克的距离不超过10^9。任意两相邻站之间的距离不超过L3。旅行最小花费不超过10^9。
output:
一个整数------最小花费。
input:
3 6 8 20 30 40
7
2 6
3
7
8
13
15
23
output:
70
【参考程序】:
#include<iostream>
using namespace std;
int l1,l2,l3,c1,c2,c3,n,s,t;
int f[10050],dis[10050];
int main()
{
scanf("%d%d%d%d%d%d",&l1,&l2,&l3,&c1,&c2,&c3);
scanf("%d",&n);scanf("%d%d",&s,&t);
for (int i=2;i<=n;i++) scanf("%d",&dis[i]);
if (s>t)
{
int tt=s;s=t;t=tt;
}
memset(f,127,sizeof(f));
f[s]=0;
for (int i=s;i<=t-1;i++)
for (int j=i+1;j<=t;j++)
{
int s=dis[j]-dis[i];
if (0<s && s<=l1)
{
if (f[j]>f[i]+c1) f[j]=f[i]+c1;
}
else if (l1<s && s<=l2)
{
if (f[j]>f[i]+c2) f[j]=f[i]+c2;
}
else if (l2<s && s<=l3)
{
if (f[j]>f[i]+c3) f[j]=f[i]+c3;
}
}
printf("%d\n",f[t]);
return 0;
}