一家工厂的流水线正在生产一种产品,这需要两种操作:操作A和操作B。每个操作只有一些机器能够完成。
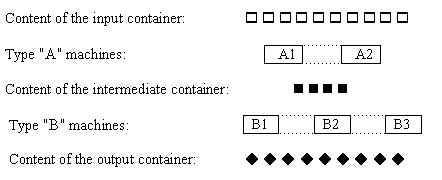
上图显示了按照下述方式工作的流水线的组织形式。A型机器从输入库接受工件,对其施加操作A,得到的中间产品存放在缓冲库。B型机器从缓冲库接受中间产品,对其施加操作B,得到的最终产品存放在输出库。所有的机器平行并且独立地工作,每个库的容量没有限制。每台机器的工作效率可能不同,一台机器完成一次操作需要一定的时间。
给出每台机器完成一次操作的时间,计算完成A操作的时间总和的最小值,和完成B操作的时间总和的最小值
input:
(file job.in)
第一行 三个用空格分开的整数:N,工件数量 (1<=N<=1000);M1,A型机器的数量 (1<=M1<=30);M2,B型机器的数量 (1<=M2<=30)。
第二行…等 M1个整数(表示A型机器完成一次操作的时间,1..20),接着是M2个整数(B型机器完成一次操作的时间,1..20)。
output:
只有一行。输出两个整数:完成所有A操作的时间总和的最小值,和完成所有B操作的时间总和的最小值(A操作必须在B操作之前完成)。
input:
5 2 3
1 1 3 1 4
output:
3 5
(转)nocow问题分析:
详尽的:http://www.nocow.cn/index.php/USACO/job
我们令delay[A][i]表示第i个A型机器的延时,显然,初始时所有delay[A]为0。然后对于所有的工件,我们选取delay[A][i]+machine[A][i](machine[A][i]表示第i个A型机器的加工用时)最小,也就是能在最快时间内完工的机器加工。更新delay[A][i]=delay[A][i]+machine[A][i](这样这个机器就进入新的一轮加工中)。在此过程中,我们用cost[A][j]记录A操作加工出第j个零件的用时。用同样的方法求出delay[B][i],cost[B][j]。
对于A操作的最短用时,显然就是cost[A]中的最大值。
因为我们在求解过程中是一个工件一个工件地送去加工,每次把一个工件送给用时最短的机器加工,那么显然有cost[A] [1]<=cost[A][2]...<=cost[A][n],同样适用于cost[B]。为了使B操作的用时最少,我们应该把A先加工出来的工件给B中加工最久的,即: cost[A][1]->cost[B][n],cost[A][2]->cost[B][n-1]......cost[A] [i]->cost[B][n-i+1] 那么 max(cost[A][i]+cost[B][n-i+1]) i=1,2,3,4...n就是B操作的最短用时。
【参考程序】:
/*
ID:XIONGNA1
PROB:job
LANG:C++
*/
#include<iostream>
using namespace std;
int a[31],b[31],wa[31],wb[31];
int fa[1001],fb[1001];
int n,m1,m2;
int main()
{
freopen("job.in","r",stdin);
freopen("job.out","w",stdout);
scanf("%d%d%d",&n,&m1,&m2);
for (int i=1;i<=m1;i++) scanf("%d",&a[i]);
for (int i=1;i<=m2;i++) scanf("%d",&b[i]);
memset(wa,0,sizeof(wa));
memset(wb,0,sizeof(wb));
int k1,k2,mina,minb;
for (int i=1;i<=n;i++)
{
mina=wa[1]+a[1];k1=1;
for (int j=2;j<=m1;j++)
if (mina>wa[j]+a[j])
{
mina=wa[j]+a[j];
k1=j;
}
minb=wb[1]+b[1];k2=1;
for (int j=2;j<=m2;j++)
if (minb>wb[j]+b[j])
{
minb=wb[j]+b[j];
k2=j;
}
wa[k1]=mina;fa[i]=mina;
wb[k2]=minb;fb[i]=minb;
}
printf("%d ",mina);
int minans=fa[1]+fb[n];
for (int i=2;i<=n;i++)
if (minans<fa[i]+fb[n-i+1])
minans=fa[i]+fb[n-i+1];
printf("%d\n",minans);
return 0;
}