N个不同的颜色的不透明的长方形(1 <= N <= 1000)被放置在一张宽为A长为B的白纸上。这些长方形被放置时,保证了它们的边与白纸的边缘平行。所有的长方形都放置在白纸内,所以我们会看到不同形状的各种颜色。坐标系统的原点(0,0)设在这张白纸的左下角,而坐标轴则平行于边缘。
格式
PROGRAM NAME: rect1
INPUT FORMAT:
(file rect1.in)
按顺序输入放置长方形的方法。第一行输入的是那个放在底的长方形(即白纸)。
第 1 行: A , B 和 N, 由空格分开 (1 <=A, B<=10,000)
第 2 到N+1行: 为五个整数 llx, lly, urx, ury, color 这是一个长方形的左下角坐标,右上角坐标和颜色。
颜色 1和底部白纸的颜色相同。 (1 <= color <= 2500)
OUTPUT FORMAT:
(file rect1.out)
输出文件应该包含一个所有能被看到颜色连同该颜色的总面积的清单( 即使颜色的区域不是连续的),按color增序排列。
不要显示没有出现过的颜色。
SAMPLE INPUT
20 20 3
2 2 18 18 2
0 8 19 19 3
8 0 10 19 4
SAMPLE OUTPUT
1 91
2 84
3 187
4 38
INPUT EXPLANATION
请注意:被(0,0)和(2,2)所描绘的是2个单位宽、2个单位高的区域
这里有一个示意图输入:
11111111111111111111
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
11222222442222222211
11222222442222222211
11222222442222222211
11222222442222222211
11222222442222222211
11222222442222222211
11111111441111111111
11111111441111111111
'4'在(8,0)与(10,19)形成的是宽为2的区域,而不是3.(也就是说,4形成的区域包含(8,0)和(8,1) ,而不是(8,0)和(8,2)) 。
矩形切割:
此思想把矩形(a,b)看成是最先加入的矩形,颜色为1。然后每次依次加入矩形,将与其重叠的矩形分割后加入队列之后(去掉重叠的部分)。最后扫描一次队列即可得出各个颜色的面积。具体分割方法如下:
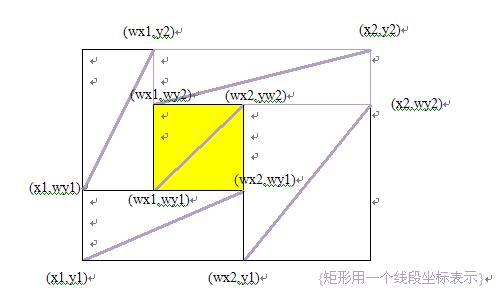
黄色区域是黄色矩形和白色矩形的重叠部分:
wx1=max(x1,wx1);
wx2=min(x2,wx2);
wy1=max(y1,wy1);
wy2=min(y2,wy2);
以上就是重叠部分的坐标。而原来的白色矩形被除去黄色区域以外,被分割成了四个小矩形。上图只是一般情况,更多的被分割出的矩形面积为0。
【参考程序】:
/*
ID: XIONGNA1
PROG: rect1
LANG: C++
*/
#include<iostream>
#include<cstring>
using namespace std;
int x1[1001],y1[1001],x2[1001],y2[1001],color[1001];
int area[2501];
int n,now;
void work(int l,int r,int b,int t,int z)
{
while (z<=n && (l>=x2[z] || r<=x1[z] || b>=y2[z] || t<=y1[z]))
z++;
if (z>n)
{
area[now]+=(r-l)*(t-b);
return ;
}
if (l<x1[z])
{
work(l,x1[z],b,t,z+1);
l=x1[z];
}
if (r>x2[z])
{
work(x2[z],r,b,t,z+1);
r=x2[z];
}
if (b<y1[z]) work(l,r,b,y1[z],z+1);
if (t>y2[z]) work(l,r,y2[z],t,z+1);
}
int main()
{
freopen("rect1.in","r",stdin);
freopen("rect1.out","w",stdout);
scanf("%d%d%d",&x2[0],&y2[0],&n);
x1[0]=y1[0]=0; color[0]=1;
for (int i=1;i<=n;i++)
scanf("%d%d%d%d%d",&x1[i],&y1[i],&x2[i],&y2[i],&color[i]);
memset(area,0,sizeof(area));
for (int i=n;i>=0;i--)
{
now=color[i];
work(x1[i],x2[i],y1[i],y2[i],i+1);
}
for (int i=1;i<=2500;i++)
if (area[i]) printf("%d %d\n",i,area[i]);
return 0;
}