高高的星空,簇簇闪耀的群星形态万千。一个星座(cluster)是一群连通的星组成的非空集合,所谓连通是指水平,垂直或者对角相邻。一个星座不能是另一个更大星座的一部分。星座可以相似(similar)。如果两个星座有相同的形状,而且包括相同数目的星体,那么不管其方向性如何,就算相似。一般而言,星座可能的方向有八个,如图1所示。
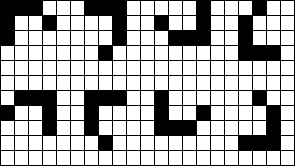
图1 相似的八个星座
夜空可以表示为一份天体图(sky map),它是一个由字符0和1组成的二维矩阵,字符1表示所在的位置有一颗星;字符0表示该位置上没有星。任务给定一份天体图,用同一个小写英文标识(mark)相似的所有星座。相似的星座必须用相同的字母标识,不同的星座表示为不同的字母。标识一个星座,就是将其中各星体对应的字符1替换为相应的小写字母。
INPUT FORMAT
文件的前两行分别记录了天体图的宽度W、深度H。而天体图则是由接下来的H行表示,每行包括W个字符。
OUTPUT FORMAT
输出文件记录了天体图与文件STARRY.IN相似,不同之处在于,各个星座按照“任务”中的要求进行了标识(mark)。
SAMPLE INPUT (file starry.in)
23
15
10001000000000010000000
01111100011111000101101
01000000010001000111111
00000000010101000101111
00000111010001000000000
00001001011111000000000
10000001000000000000000
00101000000111110010000
00001000000100010011111
00000001110101010100010
00000100110100010000000
00010001110111110000000
00100001110000000100000
00001000100001000100101
00000001110001000111000

SAMPLE OUTPUT (file starry.out)
a000a0000000000b0000000
0aaaaa000ccccc000d0dd0d
0a0000000c000c000dddddd
000000000c0b0c000d0dddd
00000eee0c000c000000000
0000e00e0ccccc000000000
b000000e000000000000000
00b0f000000ccccc00a0000
0000f000000c000c00aaaaa
0000000ddd0c0b0c0a000a0
00000b00dd0c000c0000000
000g000ddd0ccccc0000000
00g0000ddd0000000e00000
0000b000d0000f000e00e0b
0000000ddd000f000eee000
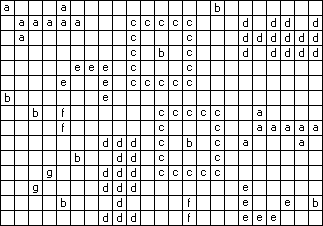
这是上述输入实例的一个可能的结果。请注意,该输出文件对应于下面的天空景象。
Constraints
0 <= W (天体图的宽度) <= 100
0 <= H (天体图的深度) <= 100
0 <= 星座的数目 <= 500
0 <= 不相似的星座数目 <= 26 (a..z)
1 <= 各星座包含的星体数目 <= 160
【参考程序】:
/*
ID: XIONGNA1
PROG: starry
LANG: C++
*/
#include <iostream>
#include <cstring>
using namespace std;
struct node
{
int left,top,down,right;
int num;
node():left(1000),top(1000),down(-1),right(-1),num(0){}
}m[600];
int n,h,w;
char s[200][200],C[600];;
int S[200][200],V[600],S2[200][200];
void flood(int i,int j,int n)
{
if(i<0||j<0||i>=h||j>=w)return;
if(s[i][j]=='0')return;
s[i][j]='0';S[i][j]=n;
flood(i-1,j-1,n); flood(i,j-1,n);
flood(i-1,j,n); flood(i+1,j+1,n);
flood(i,j+1,n); flood(i+1,j,n);
flood(i-1,j+1,n); flood(i+1,j-1,n);
}
void pretreat()
{
memset(S,-1,sizeof(S));
n=0;
for(int i=0;i<h;++i)
for(int j=0;j<w;++j)
if(s[i][j]=='1')flood(i,j,n++);
for(int i=0;i<h;++i)
for(int j=0;j<w;++j)
{
if(-1==S[i][j])continue;
node& now=m[S[i][j]];
now.num++;
if(i<now.top)now.top=i;
if(i>now.down)now.down=i;
if(j<now.left)now.left=j;
if(j>now.right)now.right=j;
}
}
bool maybe(int i,int j)
{
if(m[i].num!=m[j].num)return false;
if(m[i].left-m[i].right==m[j].left-m[j].right&&m[i].top-m[i].down==m[j].top-m[j].down)return true;
if(m[i].left-m[i].right==m[j].top-m[j].down&&m[i].top-m[i].down==m[j].left-m[j].right)return true;
return false;
}
//每个图形都可以下四种基本图形经过后三种旋转得到,所以只需四种即可
void turn0(int Left,int Right,int Top,int Down)
{//不翻转
for(int i=Top;i<=Down;++i)
for(int j=Left;j<=Right;++j)
S2[i][j]=S[i][j];
}
void turn1(int Left,int Right,int Top,int Down)
{//左右对称翻转
for(int i=0;i<=Right-Left;++i)
for(int k=Top;k<=Down;++k)
S2[k][Right-i]=S[k][Left+i];
}
void turn2(int Left,int Right,int Top,int Down)
{//左右对称翻转
for(int i=0;i<=Down-Top;++i)
for(int k=Left;k<=Right;++k)
S2[Down-i][k]=S[Top+i][k];
}
void turn3(int Left,int Right,int Top,int Down)
{//中心对称翻转
for(int i=0;i<=Right-Left;++i)
for(int j=0;j<=Down-Top;++j)
S2[Down-j][Right-i]=S[Top+j][Left+i];
}
bool exact1(int a,int b)
{
for(int i=0;i<=m[a].down-m[a].top;++i)
for(int j=0;j<=m[a].right-m[a].left;++j)
if((a==S2[m[a].top+i][m[a].left+j])^(b==S[m[b].top+i][m[b].left+j]))
return false;
return true;
}
bool exact2(int a,int b)
{
for(int i=0;i<=m[a].down-m[a].top;++i)
for(int j=0;j<=m[a].right-m[a].left;++j)
if((a==S2[m[a].top+i][m[a].left+j])^(b==S[m[b].top+j][m[b].left+i]))
return false;
return true;
}
bool exact(int i,int j)
{
if(m[i].left-m[i].right==m[j].left-m[j].right)
{
turn0(m[i].left,m[i].right,m[i].top,m[i].down);
if(exact1(i,j))return true;
turn1(m[i].left,m[i].right,m[i].top,m[i].down);
if(exact1(i,j))return true;
turn2(m[i].left,m[i].right,m[i].top,m[i].down);
if(exact1(i,j))return true;
turn3(m[i].left,m[i].right,m[i].top,m[i].down);
if(exact1(i,j))return true;
}
if(m[i].left-m[i].right==m[j].top-m[j].down)
{
turn0(m[i].left,m[i].right,m[i].top,m[i].down);
if(exact2(i,j))return true;
turn1(m[i].left,m[i].right,m[i].top,m[i].down);
if(exact2(i,j))return true;
turn2(m[i].left,m[i].right,m[i].top,m[i].down);
if(exact2(i,j))return true;
turn3(m[i].left,m[i].right,m[i].top,m[i].down);
if(exact2(i,j))return true;
}
return false;
}
void solve()
{
pretreat();
for(int i=0;i<n;++i) V[i]=i;
char c='a';
for(int i=0;i<n;++i)
{
if(V[i]!=i)
{
C[i]=C[V[i]]; continue;
}
C[i]=c++;
for(int j=i+1;j<n;++j)
{
if(V[j]!=j)continue;
if(!maybe(i,j))continue;
if(exact(i,j)) V[j]=i;
}
}
}
void cout_ans()
{
for(int i=0;i<h;++i)
{
for(int j=0;j<w;++j)
{
if(S[i][j]==-1) putchar('0');
else putchar(C[S[i][j]]);
}
putchar('\n');
}
}
int main()
{
freopen("starry.in","r",stdin);
freopen("starry.out","w",stdout);
scanf("%d%d\n",&w,&h);
for(int i=0;i<h;++i) scanf("%s\n",s[i]);
solve();
cout_ans();
}