Description
【题目说明】
此题中出现的所有数全为整数
【题目背景】
SubRaY有一天得到一块西瓜,是长方体形的....
【题目描述】
SubRaY发现这块西瓜长m厘米,宽n厘米,高h厘米.他发现如果把这块西瓜平均地分成m*n*h块1立方厘米的小正方体,那么每一小块都会有一个营养值(可能为负,因为西瓜是有可能坏掉的,但是绝对值不超过200).
现在SubRaY决定从这m*n*h立方厘米的西瓜中切出mm*nn*hh立方厘米的一块小西瓜(一定是立方体形,长宽高均为整数),然后吃掉它.他想知道他最多能获得多少营养值.(0<=mm<=m,0<=nn<=n,0<=hh<=h.mm,nn,hh 的值由您来决定).
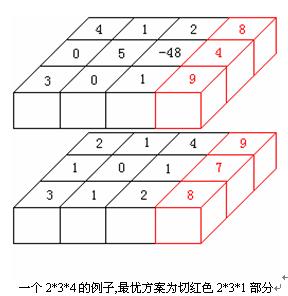
换句话说,我们希望从一个m*n*h的三维矩阵中,找出一个三维子矩阵,这个子矩阵的权和最大。
Input
首行三个数h,m,n(注意顺序),分别表示西瓜的高,长,宽.以下h部分,每部分是一个m*n的矩阵,第i部分第j行的第k个数表示西瓜第i层,第j行第k列的那块1立方厘米的小正方体的营养值。
Output
SubRaY所能得到的最大营养值
Sample Input
2 3 4
4 1 2 8
0 5 -48 4
3 0 1 9
2 1 4 9
1 0 1 7
3 1 2 8
Sample Output
45
Hint
【数据范围】
对于30%的数据,h=1,1<=m,n<=10
对于全部的数据,1<=h<=32,1<=m,n<=50,保证h<=m,n。
分析:
把三维的每个高(竖的下来的那些列,不是y坐标那个列)的和存放到二维数组中,再用二维的最大子矩阵即可。(好像废话^_^)
【参考程序】:
#include<cstring>
#include<cstdio>
#include<iostream>
#define INF -25000000
using namespace std;
int sum[60][60][60],he[60][60][60],s[60][60];
int h,m,n,ans;
int Maxsum1(int *a)
{
int sums=INF,ss=0;
for (int i=1;i<=n;i++)
{
if (ss>0) ss+=a[i];
else ss=a[i];
if (ss>sums) sums=ss;
}
return sums;
}
int Maxsum2(int a[][60])
{
int sums=INF,ss,F[60];
for (int i=1;i<=m;i++)
{
memset(F,0,sizeof(F));
for (int j=i;j<=m;j++)
{
for (int k=1;k<=n;k++) F[k]+=a[j][k];
/*ss=0;
for (int k=1;k<=n;k++)
if (ss>0) ss+=F[k];
else ss=F[k];*/
ss=Maxsum1(F);
if (ss>sums) sums=ss;
}
}
return sums;
}
int Maxsum3()
{
int sums=INF,ss;
for (int i=1;i<=h;i++)
for (int j=i;j<=h;j++)
{
for (int i1=1;i1<=m;i1++)
for (int j1=1;j1<=n;j1++)
s[i1][j1]=sum[j][i1][j1]-sum[i-1][i1][j1];
ss=Maxsum2(s);
if (sums<ss) sums=ss;
}
return sums;
}
int main()
{
scanf("%d%d%d",&h,&m,&n);
for (int i=1;i<=h;i++)
for (int j=1;j<=m;j++)
for (int k=1;k<=n;k++)
scanf("%d",&he[i][j][k]);
for (int i=1;i<=m;i++)
for (int j=1;j<=n;j++)
sum[1][i][j]=he[1][i][j];
for (int i=2;i<=h;i++)
for (int j=1;j<=m;j++)
for (int k=1;k<=n;k++)
sum[i][j][k]=sum[i-1][j][k]+he[i][j][k];
ans=Maxsum3();
printf("%d\n",ans);
return 0;
}