http://www.vijos.cn/Problem_Show.asp?id=1144
描述 Description
huyichen世子事件后,xuzhenyi成了皇上特聘的御前一品侍卫。
皇宫以午门为起点,直到后宫嫔妃们的寝宫,呈一棵树的形状;有边相连的宫殿间可以互相望见。大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是xuzhenyi手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助xuzhenyi布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式 Input Format 输入文件中数据表示一棵树,描述如下:
第1行 n,表示树中结点的数目。
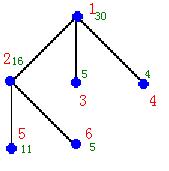
第2行至第n+1行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号i(0<i<=n),在该宫殿安置侍卫所需的经费k,该边的儿子数m,接下来m个数,分别是这个节点的m个儿子的标号r1,r2,...,rm。
对于一个n(0 < n <= 1500)个结点的树,结点标号在1到n之间,且标号不重复。
输出格式 Output Format
输出文件仅包含一个数,为所求的最少的经费。
Input:
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
Output:
25
分析:
大概思路,分三种情况,某个节点可能的三种情况,一是自己染色,二是由子
节点染色,三是自己不染色,也不由子节点来担心,就把这个任务交给该节点的父
节点了,这三种情况用不同的域来存。
第一规划:该节点自己染色,子节点们就用自己三个域中的最小值(想一想为
什么)
第二规划:该节点由孩子来染色,但是由哪一个孩子来染色呢?不知道吧,那
就枚举先,枚举子节点作为控制父节点的节点,其他节点全部用作能染色的类型,
累加选最小的。
第三规划:自己不染色,孩子也不来,就把这个任务交给父节点,那么该节点
没有染色,该节点的子节点就必须能够自己染色,这种自己染色的情况又有两种,
选一种最小的累加起来。
【参考程序】:
#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
const int Max=100000000;
int last[1600],money[1600],F[1600][4];
int pre[3200],child[3200];
bool vis[1600];
int n,root;
int Min(int x,int y)
{
return x<y?x:y;
}
void dfs(int x)
{
int y,y1,sum,num,dis;
vis[x]=true; F[x][1]=money[x];
F[x][2]=0; F[x][3]=0; num=0; sum=0;
y1=last[x];
while (last[x]>0)
{
y=child[last[x]];
if (!vis[y])
{
dfs(y); num++;
F[x][1]+=Min(F[y][1],Min(F[y][2],F[y][3]));
F[x][2]+=Min(F[y][2],F[y][1]);
if (F[y][2]==Min(F[y][1],F[y][2])) sum++;
F[x][3]+=F[y][2];
if (F[x][3]>Max) F[x][3]=Max;
}
last[x]=pre[last[x]];
}
if (sum==num && y1>0)
{
dis=0xFFFFFFF;
last[x]=y1;
while (last[x]>0)
{
y=child[last[x]];
if (F[y][1]-F[y][2]<dis) dis=F[y][1]-F[y][2];
last[x]=pre[last[x]];
}
F[x][2]+=dis;
}
else if (y1==0) F[x][2]=Max;
}
int main()
{
//freopen("guard.in","r",stdin);
//freopen("guard.out","w",stdout);
scanf("%d",&n); root=n*(n+1)/2;
int c=0,x,y,k;
memset(vis,false,sizeof(vis));
memset(last,0,sizeof(last));
memset(pre,0,sizeof(pre));
for (int i=1;i<=n;i++)
{
scanf("%d",&x); scanf("%d",&money[x]);
scanf("%d",&k);
for (int j=1;j<=k;j++)
{
scanf("%d",&y);
c++; pre[c]=last[x]; child[c]=y; last[x]=c;
c++; pre[c]=last[y]; child[c]=x; last[y]=c;
if (!vis[y])
{
root-=y; vis[y]=true;
}
}
}
memset(vis,false,sizeof(vis));
dfs(root);
printf("%d\n",Min(F[root][1],F[root][2]));
return 0;
}