[问题描述]:
如图,A 点有一个过河卒,需要走到目标 B 点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如上图的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点(图中的P1,P2 … P8 和 C)。卒不能通过对方马的控制点。
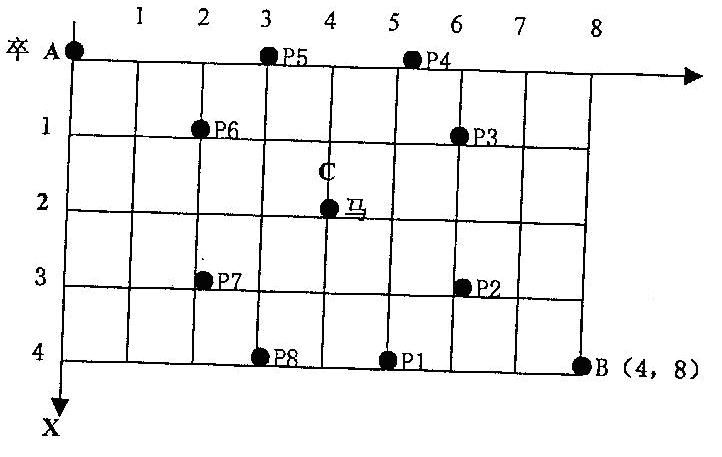
棋盘用坐标表示,A 点(0,0)、B 点(n,m)(n,m 为不超过 20 的整数,并由键盘输入),同样马的位置坐标是需要给出的(约定: C<>A,同时C<>B)。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。
[输入]:
键盘输入
B点的坐标(n,m)以及对方马的坐标(X,Y){不用判错}
[输出]:
屏幕输出
一个整数(路径的条数)。
[输入输出样例]:
输入:
6 6 3 2
输出:
17
【参考程序】:
#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
const int dx[8]={2,1,-1,-2,-2,-1,1,2};
const int dy[8]={1,2,2,1,-1,-2,-2,-1};
__int64 F[30][30];
int g[30][30];
int n,m,x2,y2;
int main()
{
//freopen("p41.in","r",stdin);
//freopen("p41.out","w",stdout);
scanf("%d%d%d%d",&n,&m,&x2,&y2);
memset(g,0,sizeof(g));
int tx,ty;
g[x2][y2]=1;
for (int i=0;i<=7;i++)
{
tx=x2+dx[i]; ty=y2+dy[i];
if (tx>=0 && tx<=n && ty>=0 && ty<=m)
g[tx][ty]=1;
}
if (g[0][0]==0) F[0][0]=1;
for (int i=1;i<=n;i++)
if (g[i][0]==0) F[i][0]=F[i-1][0];
else F[i][0]=0;
for (int i=1;i<=m;i++)
if (g[0][i]==0) F[0][i]=F[0][i-1];
else F[0][i]=0;
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
if (g[i][j]==0) F[i][j]=F[i-1][j]+F[i][j-1];
else F[i][j]=0;
printf("%I64d\n",F[n][m]);
return 0;
}