Permutation—全排列
l 简介
一个全排列是从一个有限集中选取元素,组成一个有序的序列,并且所有的元素出现且仅出现一次。
l 全排列的计数
n 当集合中元素互异时,显然全排列总共有n!个。
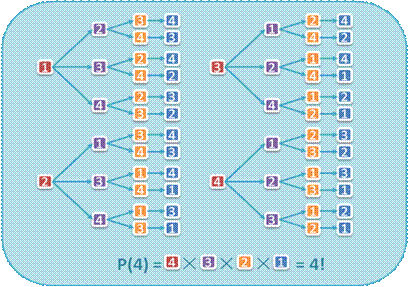
n 现在考虑集合中存在重复元素的情况:
1. 我们首先看一个简单的例子。
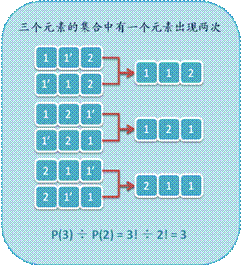
2. 设例子中的全排列数为P,那么我们将这P个排列中重复的元素1看成互异的,假设标记为1和1’,那么对于每种排列都能生成P(2) = 2!个惟一的新排列,而这些新排列恰好构成了3个互异元素的全排列,因此P = P(3) ÷P(2) = 3。
3. 假设n个元素的多重集合中有m个互异的元素,各元素出现的次数分别为a1, a2, … , am,且满足(a1 + a2 + … + am) = n那么这个集合形成的全排列个数为
4. 当m = n时,上式的结果即为n!。
l 生成全排列
n 递推生成:每次输出当前序列的下个全排列,直到生成所有全排列。
1. 按字典序生成:生成输入序列按字典序的下个全排列。
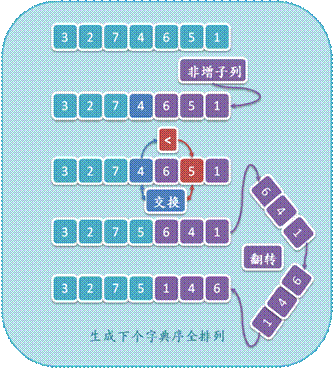
l 寻找从序列A末尾开始的最长非增连续子列S。保存子列S之前的一个元素为a,在上图中,S = { 6, 5, 1 },a = 4;
l 容易看出S是其元素的字典序最大全排列,如图中的{ 6, 5, 1 },因此无法通过在S内部交换元素得到A的下个字典序全排列,因此只需找出a + S,即序列{ 4, 6, 5, 1 }中的下个全排列。从序列末尾开始,寻找第一个大于a的元素b,如图中的5,交换a与b。这样我们更新了S之前的一个元素,只要将S变为其元素的字典序最小全排列即可得到A的下个字典序全排列;
l 翻转S,由于S为非增的(交换a与b后还是如此),那么翻转后自然变成非减序列,即其元素的字典序最小全排列。
l 以上算法即C++中std::next_permutation函数的实现。
2. 无序生成:生成输入序列的下个全排列,各全排列间并不遵循特定的顺序。
未完,待续……