题意是这样：
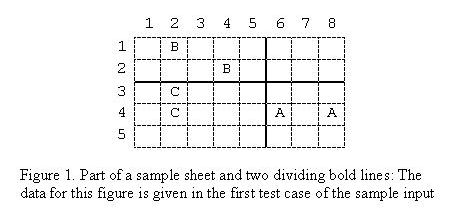
一个格板上写有k*n个字母，第i个字母有k个。然后问能否用贯穿整个方格板的横线和竖线将不同的字母分开。
解法：
首先，假设我们将k个同一个字母用一个n*m的矩形框框住，这题就转换为这样一个问题：平面上给出一些矩形，能否用用一些水平或竖直线将平面划分开，使得每一个区域中有且仅有一个矩形。
下面的想法就有点巧妙，首先，横向的切割与纵向的切割是相互独立的，就是说，无论水平线怎么画与竖直线的安排无关。
我们来考虑什么时候该横向切割，当两个方块在x方向存在着交集，（举个例子，矩形A的x范围为[x1,x2]，矩形B的x范围为[x3,x4]，x3>x1且x3<x2，这就是说，A和B在x方向上存在交集，不一定两个矩形真的相交，而是公用了某个x轴区域，我们就无法从纵向上将这两个矩形分开，因此必须从横向分割）
求交集还是用经典的排序+扫描，嘿嘿，看代码吧~(viaxl别喷我，我错了)
代码：
1
# include <cstdio>
2using namespace std;
3# include <algorithm>
4# include <vector>
5# define INF 0xfffffff
6struct ret
7
{
8
pair<int,int> left,right;
9
}data[26];
10bool cmpx(const ret &a,const ret &b)
11{
12 if(a.left.first!=b.left.first) return a.left.first<b.left.first;
13 else return a.right.first<b.right.first;
14}
15bool cmpy(const ret &a,const ret &b)
16{
17 if(a.left.second!=b.left.second) return a.left.second<b.left.second;
18 else return a.right.second<b.right.second;
19}
20int x[100],y[100],c1,c2,n,k;
21bool spiltx(const ret &a,const ret &b)
22{
23 int *end=upper_bound(x,x+c1,max(a.left.first,b.left.first)),*begin=lower_bound(x,x+c1,min(a.right.first,b.right.first));
24 for(int i=begin-x;i<end-x;i++)
25
{
26 bool flag=true;
27 for(int j=0;j<n;j++)
28 if(x[i]>data[j].left.first&&x[i]<data[j].right.first)
29 flag=false;
30 if(flag) return true;
31
}
32 return false;
33
34}
35bool spilty(const ret &a,const ret &b)
36{
37 int *end=upper_bound(y,y+c2,max(a.left.second,b.left.second)),*begin=lower_bound(y,y+c2,min(a.right.second,b.right.second));
38 for(int i=begin-y;i<end-y;i++)
39 {
40 bool flag=true;
41 for(int j=0;j<n;j++)
42 if(y[i]>data[j].left.second&&y[i]<data[j].right.second)
43 flag=false;
44 if(flag) return true;
45 }
46 return false;
47
48}
49int main()
50{
51 int test;
52 scanf("%d",&test);
53 while(test--)
54 {
55 c1=c2=0;
56 scanf("%d%d",&n,&k);
57 for(int i=0;i<n;i++)
58 {
59 data[i].left.first=data[i].left.second=INF;
60 data[i].right.first=data[i].right.second=-1;
61 for(int j=0;j<k;j++)
62 {
63 int tx,ty;
64 scanf("%d%d",&tx,&ty);
65 data[i].left.first=min(data[i].left.first,tx);
66 data[i].left.second=min(data[i].left.second,ty);
67 data[i].right.first=max(data[i].right.first,tx);
68 data[i].right.second=max(data[i].right.second,ty);
69 }
70 data[i].left.first--;
71 data[i].left.second--;
72 x[c1++]=data[i].left.first;
73 x[c1++]=data[i].right.first;
74 y[c2++]=data[i].left.second;
75 y[c2++]=data[i].right.second;
76 }
77 sort(x,x+c1);
78 sort(y,y+c1);
79 c1=unique(x,x+c1)-x;
80 c2=unique(y,y+c2)-y;
81 bool flag=true;
82 //judge x
83 sort(data,data+n,cmpy);
84 int m=data[0].right.second,last=0;
85 for(int i=1;i<n;i++)
86 {
87 if(data[i].left.second<m)
88 m=max(m,data[i].right.second);
89 else
90 {
91 for(int j=last;j<i;j++)
92 for(int k=j+1;k<i;k++)
93 if(!spiltx(data[j],data[k]))
94 flag=false;
95 m=data[i].right.second;
96 last=i;
97 }
98 }
99 for(int j=last;j<n;j++)
100 for(int k=j+1;k<n;k++)
101 if(!spiltx(data[j],data[k]))
102 flag=false;
103 //judgey
104 sort(data,data+n,cmpx);
105 m=data[0].left.first;
106 last=0;
107 for(int i=1;i<n;i++)
108 {
109 if(data[i].left.first<m)
110 m=max(m,data[i].right.first);
111 else
112 {
113 for(int j=last;j<i;j++)
114 for(int k=j+1;k<i;k++)
115 if(!spilty(data[j],data[k]))
116 flag=false;
117 m=data[i].right.first;
118 last=i;
119 }
120 }
121 for(int j=last;j<n;j++)
122 for(int k=j+1;k<n;k++)
123 if(!spilty(data[j],data[k]))
124 flag=false;
125 if(flag) printf("YES\n");
126 else printf("NO\n");
127 }
128 return 0;
129}