题意：
给出一段圆弧的起点、终点以及第三点（三点不共线），求4个点在整点的最小矩形将其围住。
测试数据：
/Files/yzhw/cover.rar解法：
首先，肯定要求圆心的
大家数学都很牛，我就给一个图，一个式子，你懂的
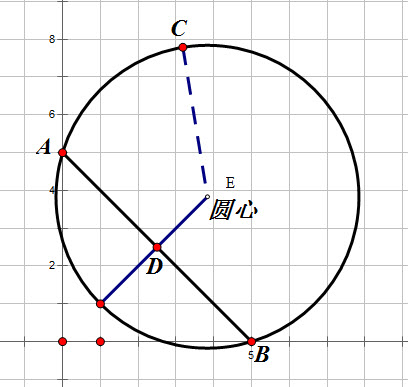
CE
2=DB
2+DE
2然后用解析法做吧- -，要讨论下A、B是否为水平线或者竖直线
下面就是确定上下左右整点坐标的问题了
还记得math库里有atan2?嘻嘻，那就好办了
要分两种情况讨论，
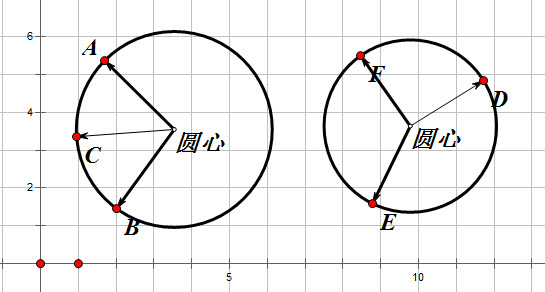
A、B是弧的端点。
也许这两种情况从几何上看MS一样的，但是对于求atan2就不同了
大家知道，atan2返回值是-PI~PI
也就是说，（-1,0）向量返回PI，（1,0）返回0，然后（-1,0）向逆时针方向转一点点就是返回接近-PI的数了，-PI和PI是同一点，但atan2处理的时候PI位置是闭区间，而-PI位置是开区间。
废话了一堆，大家应该明白了，上图第一种情况C的atan2值是大于a、b的最大值或者小于a、b的最小值的，而第二种情况d的atan2值是介于e、f之间的。
分类讨论，然后分别测试-PI向量、PI/2向量、0向量、-PI/2向量是否在圆弧内就可以了。
一个值得注意的地方，下取整应该使用floor函数，应为如果直接int取整，当浮点值小于0的时候就变成上取整了- -
我感觉自己的代码写的很到位的，再有不懂得大家看我代码吧，不过话说java的效率真蛋疼。。一个O（1）的算法竟然能跑5秒。。。
代码：
1
Source Code
2
3Problem: 1266 User: yzhw
4Memory: 3024K Time: 5422MS
5Language: Java Result: Accepted
6
7Source Code
8import java.util.*;
9
public class Main 
{
10
11
/** *//**
12 * @param args
13
*/
14 static int x1,x2,x3,y1,y2,y3,left,right,up,down;
15 static double x,y,x4,y4,d,r;
16 static double dis(double x1,double y1,double x2,double y2)
17 {
18 return Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
19 }
20 static double cross(double x1,double y1,double x2,double y2)
21 {
22 return x1*y2-x2*y1;
23 }
24 static boolean gt(double num,double pos)
25 {
26 return Math.abs(num-pos)<1e-6||num>pos;
27 }
28 static boolean le(double num,double pos)
29 {
30 return Math.abs(num-pos)<1e-6||num<pos;
31 }
32 static int floor(double num)
33 {
34 num+=1e-8;
35 int res=(int)Math.floor(num);
36 if(Math.abs(res-num)<1e-6) return res;
37 else return res+1;
38 }
39 public static void main(String[] args) {
40 Scanner in=new Scanner (System.in);
41 x1=in.nextInt();
42 y1=in.nextInt();
43 x2=in.nextInt();
44 y2=in.nextInt();
45 x3=in.nextInt();
46 y3=in.nextInt();
47 x4=(x1+x2)*0.5;
48 y4=(y1+y2)*0.5;
49 d=dis(x1,y1,x4,y4);
50 if(x1==x2)
51 {
52 y=(y1+y2)*0.5;
53 x=(d*d+x4*x4+y4*y4-x3*x3-y3*y3-y*2.0*(y4-y3))*0.5/(x4-x3);
54 }
55 else if(y1==y2)
56 {
57 x=(x1+x2)*0.5;
58 y=(d*d+x4*x4+y4*y4-x3*x3-y3*y3-x*2.0*(x4-x3))*0.5/(y4-y3);
59 }
60 else
61 {
62 double k=(x1-x2)/(double)(y2-y1);
63 double t=d*d+x4*x4+y4*y4-x3*x3-y3*y3-2.0*(y4-y3)*(y4-k*x4);
64 x=t/(2.0*(x4-x3)+2.0*(y4-y3)*k);
65 y=k*x+y4-k*x4;
66 }
67 r=dis(x3,y3,x,y);
68 //System.out.println(x+" "+y+" "+r);
69 double start=Math.atan2(y1-y, x1-x),end=Math.atan2(y2-y, x2-x),nxt=Math.atan2(y3-y,x3-x);
70 if(le(nxt,Math.min(start,end))||gt(nxt,Math.max(start,end)))
71 {
72 if(le(Math.PI,Math.min(start,end))||gt(Math.PI,Math.max(start,end)))
73 left=(int)Math.floor(x-r+1e-8);
74 else
75 left=Math.min(x1, x2);
76 if(le(0,Math.min(start,end))||gt(0,Math.max(start,end)))
77 right=floor(x+r);
78 else
79 right=Math.max(x1, x2);
80 if(le(-Math.PI*0.5,Math.min(start,end))||gt(-Math.PI*0.5,Math.max(start,end)))
81 down=(int)Math.floor(y-r+1e-8);
82 else
83 down=Math.min(y1, y2);
84 if(le(Math.PI*0.5,Math.min(start,end))||gt(Math.PI*0.5,Math.max(start,end)))
85 up=floor(y+r);
86 else
87 up=Math.max(y1, y2);
88 }
89 else
90 {
91 if(le(Math.PI,Math.max(start,end))&>(Math.PI,Math.min(start,end)))
92 left=(int)Math.floor(x-r+1e-8);
93 else
94 left=Math.min(x1, x2);
95 if(le(0,Math.max(start,end))&>(0,Math.min(start,end)))
96 right=floor(x+r);
97 else
98 right=Math.max(x1, x2);
99 if(le(-Math.PI*0.5,Math.max(start,end))&>(-Math.PI*0.5,Math.min(start,end)))
100 down=(int)Math.floor(y-r+1e-8);
101 else
102 down=Math.min(y1, y2);
103 if(le(Math.PI*0.5,Math.max(start,end))&>(Math.PI*0.5,Math.min(start,end)))
104 up=floor(y+r);
105 else
106 up=Math.max(y1, y2);
107 }
108 System.out.println((right-left)*(up-down));
109 }
110
111
}
112
113