|
Given a plane
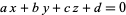 |
(1)
|
and a point 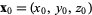 , the normal to the plane is given by , the normal to the plane is given by
![v=[a; b; c],](http://mathworld.wolfram.com/images/equations/Point-PlaneDistance/NumberedEquation2.gif) |
(2)
|
and a vector from the plane to the point is given by
![w=-[x-x_0; y-y_0; z-z_0].](http://mathworld.wolfram.com/images/equations/Point-PlaneDistance/NumberedEquation3.gif) |
(3)
|
Projecting 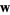 onto onto 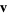 gives the distance gives the distance 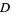 from the point to the plane as from the point to the plane as
Dropping the absolute value signs gives the signed distance,
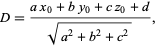 |
(9)
|
which is positive if  is on the same side of the plane as the normal vector is on the same side of the plane as the normal vector 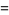 and negative if it is on the opposite side. and negative if it is on the opposite side.
This can be expressed particularly conveniently for a plane specified in Hessian normal form by the simple equation
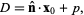 |
(10)
|
where 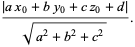 is the unit normal vector. Therefore, the distance of the plane from the origin is simply given by is the unit normal vector. Therefore, the distance of the plane from the origin is simply given by  (Gellert et al. 1989, p. 541). (Gellert et al. 1989, p. 541).
Given three points  for for 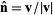 , 2, 3, compute the unit normal , 2, 3, compute the unit normal
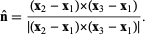 |
(11)
|
Then the distance from a point 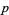 to the plane containing the three points is given by to the plane containing the three points is given by
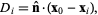 |
(12)
|
where 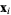 is any of the three points. Expanding out the coordinates shows that is any of the three points. Expanding out the coordinates shows that
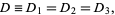 |
(13)
|
as it must since all points are in the same plane, although this is far from obvious based on the above vector equation.

Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, 1989.
|