多重背包问题，但背包大小实在太大，所以这里考虑用生成函数来做
生成函数为：
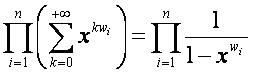
这是无法直接处理的，我们不妨将其变形，令W为w1,w2,…,wn的最小公倍数，则原式化为：
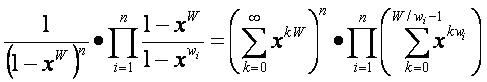
另f[r]表示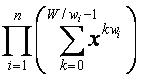
中，xr的系数，这一步是传统的多重背包，即根据剩余类分别处理，背包大小不超过nW，所以这一步的时间复杂度为O(n2W)
而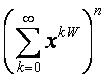
中，只有x0，xW，x2W，……的系数不为0，其中xkW的系数为组合数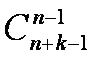
考虑n=kW+r，此时的方案数为
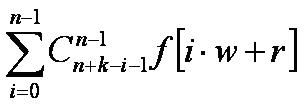
通过观察，发现，当r一定时，上式随着n单调递增
因此可以枚举r，然后二分答案求出最优解
二分时很有可能数据超过long long，有一个处理技巧就是判断a
1*a
2*...*a
n是否小于等于p时直接判断p/a
1/a
2/.../a
n是否大于等于1
#include <iostream>
#include <cstdlib>
using namespace std;
int n,w[10],W;
long long f[200000];
int gcd(int a,int b)
{
while(b) { int t=a%b; a=b; b=t; }
return a;
}
bool check(long long k,int r,long long p)
{
long long tp;
int i,j;
for(i=0;i<n;i++)
{
if (k<i) break;
if (f[i*W+r]==0) continue;
tp=p/f[i*W+r];
for(j=1;j<=n-1;j++)
tp*=j;
for(j=1;j<n;j++)
tp/=j+k-i;
if (tp==0) return true;
tp=f[i*W+r];
for(j=1;j<n;j++)
tp*=j+k-i;
for(j=1;j<=n-1;j++)
tp/=j;
p-=tp;
}
return p==0;
}
int main(void)
{
int m,i,j,k,t,u=0,r;
long long lt,rt,mt;
long long sum,p,res;
while(scanf("%d",&n),n)
{
u++;
W=1;
for(i=1;i<=n;i++)
{
scanf("%d",w+i);
W*=w[i]/gcd(W,w[i]);
}
for(i=0;i<n*W;i++)
f[i]=0;
f[0]=1;
for(i=1;i<=n;i++)
{
if (w[i]==W) continue;
for(r=0;r<w[i];r++)
{
k=n*W-w[i]+r; sum=0;
for(j=w[i];j<W;j+=w[i])
sum+=f[k-j];
f[k]+=sum;
for(k-=w[i];k>=0;k-=w[i])
{
sum-=f[k];
if ((t=k+w[i]-W)>=0)
sum+=f[t];
f[k]+=sum;
}
}
}
printf("Set %d\n",u);
scanf("%d",&m);
while(m--)
{
scanf("%I64d",&p);
res=p*100+1;
for(r=0;r<W;r++)
{
lt=-1;
if (r==0) lt++;
rt=(res-r)/W+1;
while(lt+1<rt)
{
mt=(lt+rt)>>1;
if (check(mt,r,p))
rt=mt;
else lt=mt;
}
if (res>rt*W+r) res=rt*W+r;
}
if (res>100*p)
puts("no candy for you");
else printf("%I64d\n",res);
}
}
return 0;
}
posted on 2010-10-06 18:16
zxb 阅读(1112)
评论(0) 编辑 收藏 引用