这是一个简单的生存游戏,你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下:
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走,并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后,当他走到这条路径的终点时,他将只有终点所标记的能量。
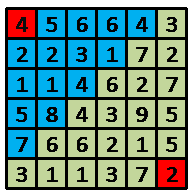
如上图,机器人一开始在(1,1)点,并拥有4单位能量,蓝色方块表示他所能到达的点,如果他在这次路径选择中选择的终点是(2,4)
点,当他到达(2,4)点时将拥有1单位的能量,并开始下一次路径选择,直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数,输出的结果对10000取模。