http://acm.hdu.edu.cn/showproblem.php?pid=3411 浙江理工邀请赛G题,又是一道比赛的时候没有做出来的题目,当时思路被题目给的公式限制住了,一看有除法又要取模,而且数据都很大,觉得没有办法入手,就跳过了。赛后,发现是可以构造矩阵做-_-||| 唉,被题目给的公式限制了思路啊。。。 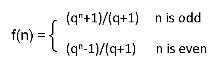 设 An = (-q)^n Sn = sigma ( Ai ),i = 0, 1,..., n | Sn | = | 1, 1 | * | Sn-1 | | An+1| | 0, -q | | An | Sn = ( 1 - ( -q )^n ) / ( 1 + q ) 则 f( n ) = | S(n-1) |, 注意是绝对值的S(n-1),因为题目中的f( n ) 是一个正数,就是因为这里没弄清楚WA了一次。 以下是我的代码:
 // | Sn | = | 1, 1 | * | Sn-1 | // | Sn | = | 1, 1 | * | Sn-1 |
 // | An+1 | | 0, -q | | An | // | An+1 | | 0, -q | | An |
 #include<iostream> #include<iostream>
 using namespace std; using namespace std;
 typedef __int64 ll; typedef __int64 ll;
 ll p; ll p;
 ll pow_mod( ll a, ll n, ll z1 ) ll pow_mod( ll a, ll n, ll z1 )
   { {
 ll ans = 1, d = a % p; ll ans = 1, d = a % p;
 while( n ) while( n )
   { {
 if( n & 1 ) ans = ( ans * d ) % p; if( n & 1 ) ans = ( ans * d ) % p;
 d = ( d * d ) % p; d = ( d * d ) % p;
 n >>= 1; n >>= 1;
 } }
 ans = ( ans + z1 ) % p; ans = ( ans + z1 ) % p;
 ans = ( p - ans ) % p; ans = ( p - ans ) % p;
 return ans; return ans;
 } }

 void matrix_mod( ll a[][2], ll b[][2] ) void matrix_mod( ll a[][2], ll b[][2] )
   { {
 ll c[2][2]; ll c[2][2];
 int i, j, k; int i, j, k;
 memset( c, 0, sizeof( c ) ); memset( c, 0, sizeof( c ) );
 for( k = 0; k < 2; k++ ) for( k = 0; k < 2; k++ )
 for( i = 0; i < 2; i++ ) for( i = 0; i < 2; i++ )
 for( j = 0; j < 2; j++ ) for( j = 0; j < 2; j++ )
 c[k][i] += a[k][j] * b[j][i]; c[k][i] += a[k][j] * b[j][i];
 for( i = 0; i < 2; i++ ) for( i = 0; i < 2; i++ )
 for( j = 0; j < 2; j++ ) for( j = 0; j < 2; j++ )
 a[i][j] = c[i][j] % p; a[i][j] = c[i][j] % p;
 } }

 ll Mod( ll x1, ll y1, ll z1, ll y2, ll z2 ) ll Mod( ll x1, ll y1, ll z1, ll y2, ll z2 )
   { {
 int i, j, k; int i, j, k;
 ll q = pow_mod( x1, y1, z1 ); ll q = pow_mod( x1, y1, z1 );
 ll a[2][2], I1[2][2], I2[2][2]; ll a[2][2], I1[2][2], I2[2][2];
 a[0][0] = 1, a[0][1] = 1, a[1][0] = 0, a[1][1] = q; a[0][0] = 1, a[0][1] = 1, a[1][0] = 0, a[1][1] = q;
 I1[0][0] = 1, I1[0][1] = 0, I1[1][0] = 0, I1[1][1] = 1; I1[0][0] = 1, I1[0][1] = 0, I1[1][0] = 0, I1[1][1] = 1;
 while( z2 ) while( z2 )
   { {
 if( z2 & 1 ) matrix_mod( I1, a ); if( z2 & 1 ) matrix_mod( I1, a );
 matrix_mod( a, a ); matrix_mod( a, a );
 z2 >>= 1; z2 >>= 1;
 } }
 a[0][0] = 1, a[0][1] = 1, a[1][0] = 0, a[1][1] = q; a[0][0] = 1, a[0][1] = 1, a[1][0] = 0, a[1][1] = q;
 I2[0][0] = 1, I2[0][1] = 0, I2[1][0] = 0, I2[1][1] = 1; I2[0][0] = 1, I2[0][1] = 0, I2[1][0] = 0, I2[1][1] = 1;
 for( i = 0; i < y2; i++ ) for( i = 0; i < y2; i++ )
   { {
 matrix_mod( I2, a ); matrix_mod( I2, a );
 matrix_mod( a, a ); matrix_mod( a, a );
 } }
 memset( a, 0, sizeof( a ) ); memset( a, 0, sizeof( a ) );
 for( i = 0; i < 2; i++ ) for( i = 0; i < 2; i++ )
 for( j = 0; j < 2; j++ ) for( j = 0; j < 2; j++ )
 for( k = 0; k < 2; k++ ) for( k = 0; k < 2; k++ )
 a[i][j] += I1[i][k] * I2[k][j]; a[i][j] += I1[i][k] * I2[k][j];
 for( i = 0; i < 2; i++ ) for( i = 0; i < 2; i++ )
 for( j = 0; j < 2; j++ ) for( j = 0; j < 2; j++ )
 a[i][j] %= p; a[i][j] %= p;
 return ( a[0][0] + a[0][1] * q ) % p; return ( a[0][0] + a[0][1] * q ) % p;
 } }

 int main( ) int main( )
   { {
 ll x1, y1, z1, y2, z2; ll x1, y1, z1, y2, z2;
 ll ans; ll ans;
 while( 1 ) while( 1 )
   { {
 scanf("%I64d%I64d%I64d",&x1,&y1,&z1); scanf("%I64d%I64d%I64d",&x1,&y1,&z1);
 if( x1 == -1 && y1 == -1 && z1 == -1 )break; if( x1 == -1 && y1 == -1 && z1 == -1 )break;
 scanf("%I64d%I64d%I64d",&y2,&z2,&p); scanf("%I64d%I64d%I64d",&y2,&z2,&p);
 ans = Mod( x1, y1, z1, y2, z2 ); ans = Mod( x1, y1, z1, y2, z2 );
 if( ( y2 == 0 && z2 % 2 == 1 ) || ( y2 != 0 && z2 % 2 == 0 ) ) if( ( y2 == 0 && z2 % 2 == 1 ) || ( y2 != 0 && z2 % 2 == 0 ) )
 ans = p - ans; ans = p - ans;
 printf("%I64d\n",ans); printf("%I64d\n",ans);
 } }
 return 0; return 0;
 } }

|