在计算机图形学中，变换矩阵是非常基础也是非常重要的知识，在许多资料中，只是罗列出一堆矩阵公式，图表等等，这很难给人感性的认识，特别是初学者，笔者结合OpenGL这样一个非常流行的图形库，以实践的方式阐述在3D变换矩阵中最简单的三种：平移、缩放以及旋转。

 

这里有一些前提知识，就是需要了解线性代数一些最最基本的知识，否则难以理解一些东西，而这些知识载体也是很容易获得的。

 

变换

我在制作3D程序的时候，任何在3D环境中的物体被图形引擎绘制的时候都是一个个3D环境中的点，而正是由于这个原因，当我们想要变换一个物体的位置，大小，方向，乃至形状的时候，我们其实只要有序的改变物体网格上的点就可以了。

 

怎样变换

在计算机图形学中，我们通常用矩阵来对3D图形的每个点进行变换，比如我们变换一个需要这样的计算步骤：

将一个点的向量与一个变换矩阵相乘

 

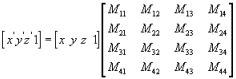
这样就得到了一个变化后的向量

 

 

 

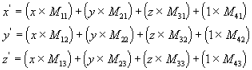
在实践中，最常用到的就是平移，缩放和旋转了。

 

下面给出这三种变换的矩阵

平移

 

缩放

 

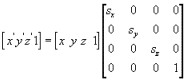
旋转

X

 

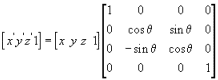
Y

 

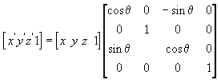
Z

 

 

学习理论的目的就是为了应用，然而在我们经常应用的3D图形库，比如D3D， OpenGL 中矩阵变换已经被封装成为调用非常简便的函数了。对于产品开发，这无疑对缩短产品周期有很大的帮助，侯捷说过一句话：“学从难处学，用从易处用”，这句话很有道理，所以我们仅仅使用OpenGL的glVertex*这样的函数将以上这些晦涩的图表应用到实践当中。

 

Demo的界面如图所示，你可以在“操作”菜单中对界面中的正方体进行平移、缩放以及旋转的操作。

 

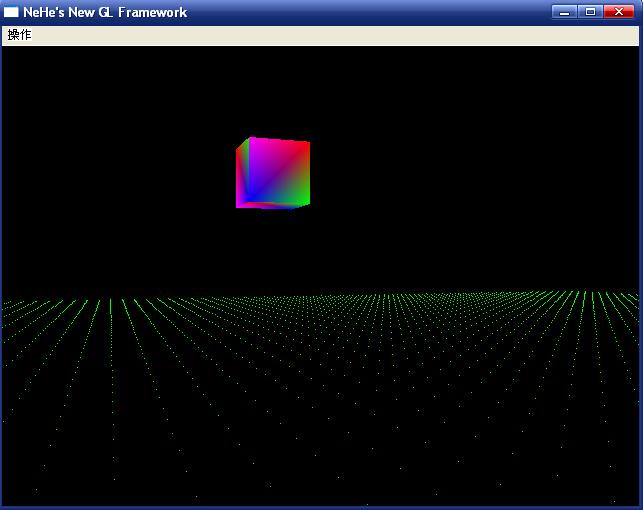因为用的是Nehe的OpenGL的代码框架（nehe.gamedev.net），对于如何建立起一个OpenGL程序，这里就不做相应的阐述了，因为这并不是本文讨论的范围。

 

下面对重要的代码段进行讲述：

 

//这里定义了正方体的各个顶点，因为不是使用glTranslate、glRotate这些函数进行变换而是手工计算变换后的物体坐标，所以我们用一个顶点数组来描述物体，这里一共有24个点，每个点都使用奇次坐标来表示(x,y,z,w)。

GLfloat Cube[24][4]={{-1.0f,1.0f,1.0f,1.0f},

{-1.0f,-1.0f,1.0f,1.0f},

{1.0f,-1.0f,1.0f,1.0f},

{1.0f,1.0f,1.0f,1.0f}, // 前表面

{-1.0f,1.0f,1.0f,1.0f},

{-1.0f,1.0f,-1.0f,1.0f},

{-1.0f,-1.0f,-1.0f,1.0f},

{-1.0f,-1.0f,1.0f,1.0f}, // 左侧面

{1.0f,1.0f,1.0f,1.0f},

{1.0f,1.0f,-1.0f,1.0f},

{1.0f,-1.0f,-1.0f,1.0f},

{1.0f,-1.0f,1.0f,1.0f}, // 右侧面

{1.0f,1.0f,1.0f,1.0f},

{1.0f,1.0f,-1.0f,1.0f},

{-1.0f,1.0f,-1.0f,1.0f},

{-1.0f,1.0f,1.0f,1.0f}, // 顶部

{1.0f,-1.0f,-1.0f,1.0f},

{-1.0f,-1.0f,-1.0f,1.0f},

{-1.0f,-1.0f,1.0f,1.0f},

{1.0f,-1.0f,1.0f,1.0f}, // 底部

{-1.0f,1.0f,-1.0f,1.0f},

{-1.0f,-1.0f,-1.0f,1.0f},

{1.0f,-1.0f,-1.0f,1.0f},

{1.0f,1.0f,-1.0f,1.0f} // 背面

};

 

//一般在3D引擎中，模型坐标系中原始的物体坐标一般需要保留，而不会随着流水线，而变成转化后的坐标，所以这里我们用一个数组来保存变换后的坐标

 

GLfloat CubeNew[24][4];

 

// 这里是一个核心函数，用来进行两个矩阵相乘的操作

// 这里涉及到矩阵相乘，这在任何一本线性代数的课本上都能够轻松的找到

void MatrixMul(GLfloat Matrix[4][4])

{

       for(int i=0;i<24;i++)

       {

       CubeNew[i][0]=Cube[i][0]*Matrix[0][0]+Cube[i][1]*Matrix[0][1]+Cube[i][2]*Matrix[0][2]+Cube[i][3]*Matrix[0][3];

       CubeNew[i][1]=Cube[i][0]*Matrix[1][0]+Cube[i][1]*Matrix[1][1]+Cube[i][2]*Matrix[1][2]+ Cube[i][3]*Matrix[1][3];

       CubeNew[i][2]=Cube[i][0]*Matrix[2][0]+Cube[i][1]*Matrix[2][1]+Cube[i][2]*Matrix[2][2]+ Cube[i][3]*Matrix[2][3];

       CubeNew[i][3]=Cube[i][0]*Matrix[3][0]+Cube[i][1]*Matrix[3][1]+Cube[i][2]*Matrix[3][2]+ Cube[i][3]*Matrix[3][3];

       }

}

 

//有了这些基本操作的函数，下面就需要进行实际的变换了，其实也十分的简单

// 平移矩阵

GLfloat Matrix_Transform[4][4]=

{{1,0,0,-3},

{0,1,0,3},

{0,0,1,1},

{0,0,0,1}};

 

// 缩放矩阵

GLfloat Matrix_Scale[4][4]=

{{1,0,0,0},

{0,2,0,0},

{0,0,3,0},

{0,0,0,1}};

 

#define PI 3.1415926

// 旋转矩阵

GLfloat Matrix_Rotate[4][4]=

{{1,0,0,0},

{0,cos(PI/15),-sin(PI/15),0},

{0,sin(PI/15),cos(PI/15),0},

{0,0,0,1}};

 

 

//在绘制部分，我们首先绘制地面

              glBegin(GL_POINTS);

              DrawBackGround();

              glEnd();

//然后通过一个循环绘制转换后的坐标

for(int x=0;x<24;x++){

                            glVertex4f(CubeNew[x][0],CubeNew[x][1],CubeNew[x][2],CubeNew[x][3]);

                     }